Iterated Tverberg Point-Theory

Abstract

这个算法是在写实验的时候要执行的，因为阅读的文档和最后的报告都是要用英文写，所以这里就用英文来写了，用的英文句子都比较简单，希望理解起来容易一些。所参照的论文，课件都在博文中说道。大家觉得算法介绍，执行不对的地方欢迎指出来共同探讨。

Iterated Tverberg point algorithm was used to compute an approximate of center point in computational geometry. Here, we use it to combine a set of models computed by machine learning algorithm to a much better model.

Definitions

Closed Halfspace is a set {x∈Rd:a⋅x≤b,a∈Rd,b∈R}.

The Tukey depth of a point x with respect to a set P is the minimum number of points of P in any halfspace containing x. In the following figure, the depth of the blue point w.r.t the black points set is 1.



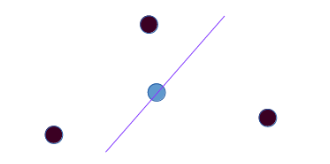
A point x is a centerpoint with respect to a set P⊂Rd if depth of x is at least nd+1.

Convex hull of a set A, denoted by conv(A), is the set of all convex combination of points in A. conv(A)={x|∃a1,...,aN∈A,α1,...,αn≥0;∑Ni=1αi=1;x=∑Ni=1αiai.}.

主要参照 http://www.cs.cmu.edu/afs/cs/academic/class/15456-s10/ClassNotes/

Theorems

这个部分的理论证明是后面算法执行必须要用的所以很必要。

Radon Theorem

Let a1,a2,...,am∈Rd, m ≥d+2, then there is a partition of {1,…,m} into I and J such that the convex hull of {ai,i∈I} and {aj,j∈J} is nonempty.

Proof: Denote bi:=(ai,1). There are m≥d+2 vectors in d+1 dimensional space,

thus they are linearly dependent. It means that there exists α1,...,αm not all zero

such that:

∑i=1mαibi=0.

Construct I={i|αi≥0} and J={j|αj<0}.

As the last coordinate of bi is 1, thus:

∑i∈Iαi+∑j∈Jαj=0.∑i∈Iαi=−∑j∈Jαj=α≠0.

Then the vector

∑i∈Iαiαai=−∑j∈Jαjαaj

is in both the convex hull of {ai|i∈I} and {aj|j∈J}, the theorem is proved.

Carathéodory Theorem

For S⊂Rd, if x∈conv(S) then x∈conv(R) for some R⊂S, |R|≤d+1.

Assume that x=∑i|xi∈Sαixi, with αi>0; ∑iαi=1 and |S|>d+1. Then there exists a set S′ of size smaller than |S|, with x∈conv(S′). Thus, we are able to reduce the size of the set whose convex hull contains x until we get R of size at most d+1.

Denote x2−x1,x3−x1,...,xd+2−x1, there are d+1 vectors in d-dimension, thus they are linearly dependent. Therefore there exists β2,...,βd+2 not all zero such that:

∑i=2d+2βi(xi−x1)=0.∑i=2d+2βixi=∑i=2d+2βix1.

Let β1=−∑i≥2βi, βj=0 for j>d+2, then

∑i=1d+2βixi=0,∑j=d+3βjxj=0.∑iβixi=0and∑iβi=0.

Then,

x=∑iαixi=∑iαixi−λ∑iβixiforallλ

x=∑i(αi−λβi)xiforallλ

Thus, we can choose a λ such that all α′=αi−λβi≥0 and at least one such value is 0. As α′i≥0,∑iα′i=∑iαi=1, we get another convex representation of x with support size smaller than |S|. Thus, the theorem is proved.

主要参照 http://www.math.cornell.edu/~eranevo/homepage/ConvNote.pdf

The Itearted Tverberg Point Algorithm

Iterated Tverberg point algorithm is as follows,



Proof of Tukey depth

Given a point p∈Rd, a proof that p has Turkey depth (at least) r with respect to S is a collection of r disjoint subsets U1,U2,...,Ur⊂S such that p∈∩rj=1conv(Uj). In the following picture, the proof of Tukey depth of blue point is 1.



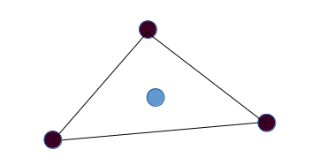
The Iterated Tverberg point Algorithm returns a point of depth at least ceiling of n2(d+1)2.

It can be seen from the algorithm that it returns a point of the desired depth and its corresponding proof if it terminates. Assume that the algorithm does not terminate. Which means that it is impossible to pick l at some time t, because every bucket has fewer than d+2 points. Let h be the maximum such that Bh is nonempty at time t. For any point p in a bucket Bi, with i∈{0,...,h}, the proof for p contains at most 2i(d+1) input points, with r=2i. Since all of the proofs in all of the buckets are disjoint, so

∑i=0h2i(d+1)2≥n.

Therefore,

2h+1−1≥n(d+1)2.

Thus,

2h>n2(d+1)2.

Then it implies that h>lgn2(d+1)2, and Blg⌈n2(d+1)2⌉ is nonempty. However, this would have caused the algorithm to break out of the while loop and terminate, contrary to our assumption. Thus, the it is proved.

The algorithm description

Any point s∈S, the set {s} is a proof of depth 1. In the algorithm, a point and its proof of depth is denoted by <point,proof>, and a collection of proofs are disjoint if their sets are pairwise disjoint. The algorithm will return a point of depth at least ceiling of n2(d+1)2 as shown before, so we initialize Bi to be empty to store points of depth 2i in the step 1 of the algorithm, for ∀i∈{0,...,lg⌈n2(d+1)2⌉}. The steps 2 and 3 of the algorithm initialize B0 with points of depth 1, and iterate the while loop until we get a point of desired depth. The steps 4 and 5 initialize the proof and get the index l, with at least d+2 points in Bl−1. Then we are able to pop out d+2 points from Bl−1, and apply Radon theorem to get Radon point c, partitions U1 and U2 in step 6 and 7. After that, we are able to iterate the two partition U1 and U2 from step 8, and start to iterate the parts of proof of each point in U1 and U2 from step 9. In steps 10 and 11, we form X as a proof that c has depth at least 2l. In steps 12 and 13, we prune the size of X to get X′ as shown in Carathéodory theorem, and push X′ to the proof. Then we push the pruned points to B0 in step 14. When the algorithm terminates, we return <c,proof> from Blg⌈n2(d+1)2⌉.

主要参照 http://www.sciencedirect.com/science/article/pii/S0925772110000349