#1078 : 线段树的区间修改
2015-09-05 10:49
218 查看
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
假设货架上从左到右摆放了N种商品,并且依次标号为1到N,其中标号为i的商品的价格为Pi。小Hi的每次操作分为两种可能,第一种是修改价格——小Hi给出一段区间[L, R]和一个新的价格NewP,所有标号在这段区间中的商品的价格都变成NewP。第二种操作是询问——小Hi给出一段区间[L, R],而小Ho要做的便是计算出所有标号在这段区间中的商品的总价格,然后告诉小Hi。
那么这样的一个问题,小Ho该如何解决呢?
提示:推动科学发展的除了人的好奇心之外还有人的懒惰心!
×Close
小Ho听完整个问题,道:“唔……既然你都说了是针对线段树问题作出的改动,那么这道题目想来就还是用线段树进行解决咯?”
小Hi叹了口气,道:“倒是没错,但是你这样进行判断真的合适么……真正应用的时候可不会有人告诉你的诶。”
小Ho笑道:“别骗我了,我们这个系列都持续这么长时间了,算法在生活中的应用场景极其有限我还是知道的。”
小Hi一副被打败的表情,又叹了一口气,道:“也是,算法就像数学一样,是能够让你知其所以然的东西,但是在实际生活中,许多问题要么太过简单,要么太过复杂,这些经典算法往往没有用武之地啊。”
看着小Hi一脸的郁闷,小Ho赶紧道:“别这样!我们还是赶紧来看今天的问题吧——既然是用线段树来解决这个问题的话,那么很容易就能想到线段树中的每一个节点维护的便是对应区间中所有商品的价值之和,这样在每次询问操作的时候,就可以使用和之前一样的方法——将询问的区间在树上分解成若干个已经计算好的区间,然后求这些区间维护的和值的和,便是我们所需要的答案。”
小Hi点了点头,道:“这部分的确和上一次的问题是一样的,但是修改操作你打算如何处理?这可就没有那么简单了!”
“这次的修改操作和之前的差别的确太大了——之前都只需要修改一个位置的值,而现在却是和询问一样,要一次性修改一个区间的值。如果仍然使用之前的方法来一个个修改的话,修改的复杂度可能会上升到O(N)呢!”小Ho忽然惊喜道:“对了,那么我就像询问一样,将修改的区间分解成若干个小区间,只修改这些区间和它们祖先结点的值不就行了么?这样的区间只会有O(logN)个,那么修改的时间复杂度也就在这个级别了!”
“你可以尝试这么做!”小Hi不怀好意的笑道。
于是小Ho回去开开心心的写了程序,但是在测试数据上折腾了很久都没有能够通过,但好在他终于发现了自己的问题所在,于是又屁颠屁颠的回来找小Hi。
“小Hi你太坏了!居然不告诉我这个问题,如果我第一次修改的是[3, 9]这个区间话,那么我就会将它拆成[3, 3], [4, 5], [6, 8], [9, 9]4个区间,那么得到修改的只有橙色的这些区间。但是如果我之后询问了[6, 7]这个区间的话,我仍然会按照修改之前的价格进行计算!”小Ho抱怨道。
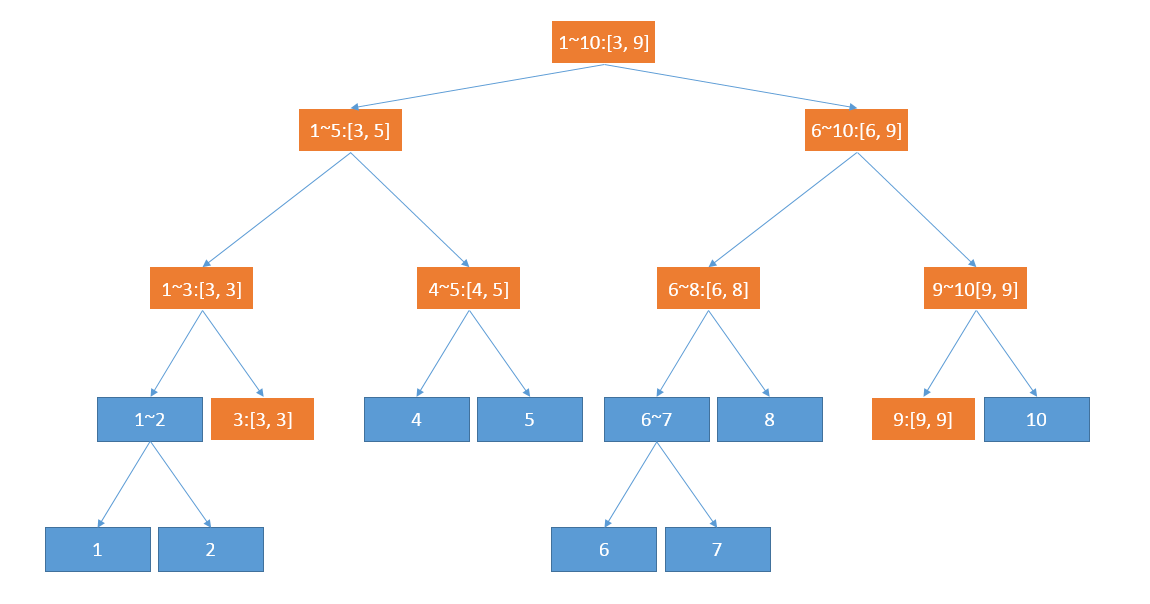
“我只是说你可以尝试这么做,可没有说这么做你就能够通过的嘛~”小Hi笑道。
小Ho无奈道:“你……那现在我该怎么解决这个问题呢?”
“你再想想——其实理论上来说,如果[3, 9]这个区间被修改的话,所有绿色的结点的值都要得到重新计算的。”小Hi重新标出了一些结点。
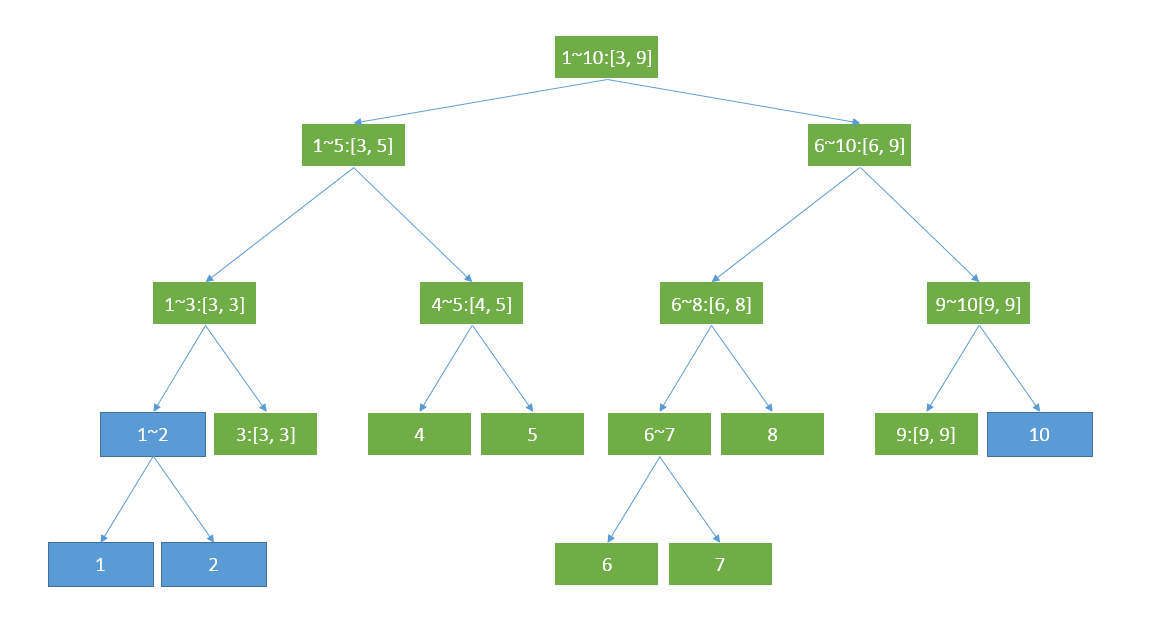
“但是实际上是没有必要这么做的——我们可以引进一种叫做Lazy Tag,即懒惰标记的东西——的确对于[3, 9]这样一次修改操作,我可以只去修改橙色的结点,但是在这个基础上,我要在[3, 9]分解出的4个区间[3, 3], [4, 5], [6, 8], [9, 9]所对应的结点上做一个懒惰标记,表示‘之前有一次操作需要将这棵子树中的所有结点的价格都进行修改,但是因为还没有用到这棵子树中的值所以我暂时不去修改’。小Hi解释道。
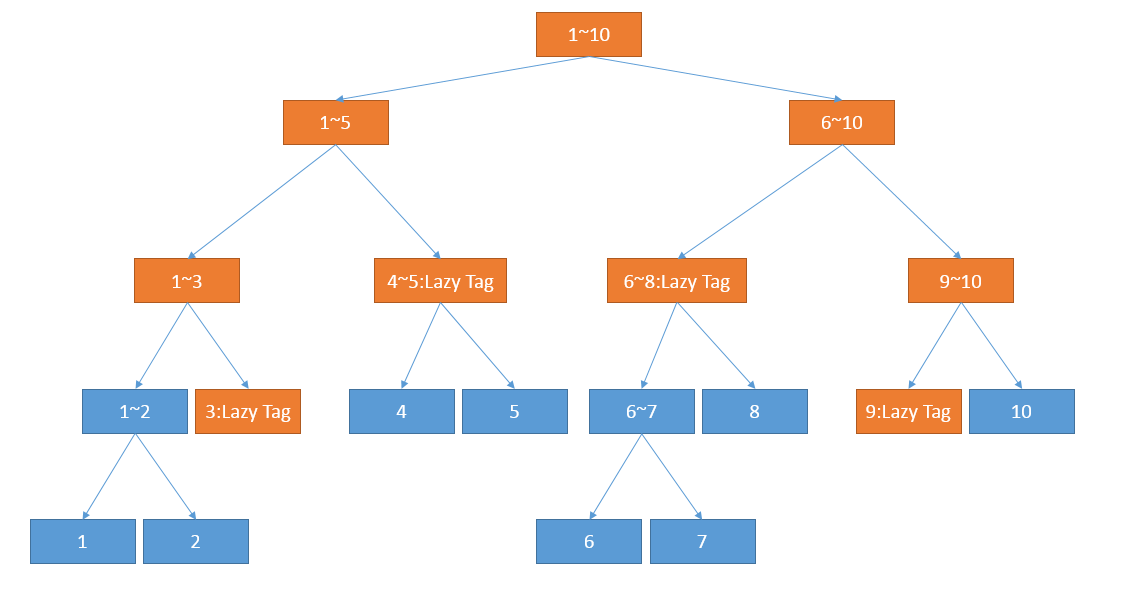
“但是这些懒惰标记又有什么用呢?”小Ho问道。
“其实就是一个暂时不处理,等到需要用到的时候再进行处理的思想。”小Hi说道:“比如你之前说道的询问了[6, 7]这个区间,那么我再从上往下分解的时候,你会发现[6, 8]这个区间上有一个懒惰标记,那么你就应该进行一个懒惰标记的‘下放操作’——也就是说去修改[6, 8]这个结点的左右儿子的值,并且同时给左右儿子添加上新的懒惰标记,然后将[6, 8]的懒惰标记去掉。”
“也就是说——本来[6, 8]的左右儿子早在之前的修改操作中就需要一同进行修改的,但是因为还没有用到单独的[6, 7],[8, 8]之类的区间的原因,所以我可以暂时不处理这些结点的修改,而是用一个懒惰标记记录下来这些结点需要进行修改这件事情。然后在之后要用到这些值的时候再进行这些操作咯?”
“是的呢!”小Hi点头道:“如果你还不清楚的话,可以来看看这段伪代码:”
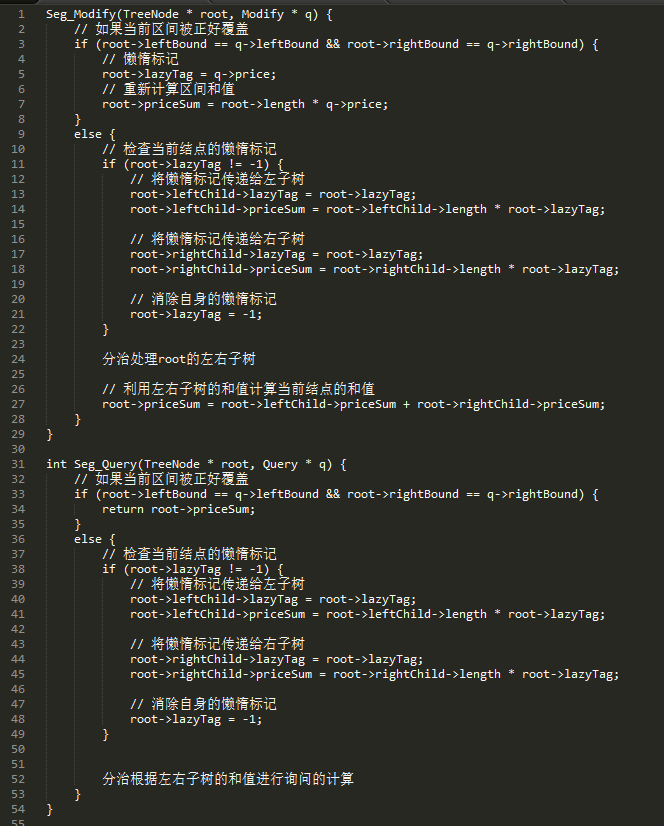
“嗯嗯!果然是这样,那么通过懒惰标记的作用,就可以将修改操作也降到O(logN)的复杂度了,那么这个问题就得到完美的解决了!”
于是小Ho哼着小曲,高兴的回去完善算法了~
Close
Save changes
每组测试数据的第1行为一个整数N,意义如前文所述。
每组测试数据的第2行为N个整数,分别描述每种商品的重量,其中第i个整数表示标号为i的商品的重量Pi。
每组测试数据的第3行为一个整数Q,表示小Hi进行的操作数。
每组测试数据的第N+4~N+Q+3行,每行分别描述一次操作,每行的开头均为一个属于0或1的数字,分别表示该行描述一个询问和一次商品的价格的更改两种情况。对于第N+i+3行,如果该行描述一个询问,则接下来为两个整数Li, Ri,表示小Hi询问的一个区间[Li, Ri];如果该行描述一次商品的价格的更改,则接下来为三个整数Li,Ri,NewP,表示标号在区间[Li, Ri]的商品的价格全部修改为NewP。
对于100%的数据,满足N<=10^5,Q<=10^5, 1<=Li<=Ri<=N,1<=Pi<=N, 0<Pi, NewP<=10^4。
样例输入
样例输出
[/code]
单点时限:1000ms
内存限制:256MB
描述
对于小Ho表现出的对线段树的理解,小Hi表示挺满意的,但是满意就够了么?于是小Hi将问题改了改,又出给了小Ho:假设货架上从左到右摆放了N种商品,并且依次标号为1到N,其中标号为i的商品的价格为Pi。小Hi的每次操作分为两种可能,第一种是修改价格——小Hi给出一段区间[L, R]和一个新的价格NewP,所有标号在这段区间中的商品的价格都变成NewP。第二种操作是询问——小Hi给出一段区间[L, R],而小Ho要做的便是计算出所有标号在这段区间中的商品的总价格,然后告诉小Hi。
那么这样的一个问题,小Ho该如何解决呢?
提示:推动科学发展的除了人的好奇心之外还有人的懒惰心!
×Close
提示:推动科学发展的除了人的好奇心之外还有人的懒惰心!
小Hi的温馨提示:在解决这个问题之前,不妨先去看看上一周的线段树介绍吧!小Ho听完整个问题,道:“唔……既然你都说了是针对线段树问题作出的改动,那么这道题目想来就还是用线段树进行解决咯?”
小Hi叹了口气,道:“倒是没错,但是你这样进行判断真的合适么……真正应用的时候可不会有人告诉你的诶。”
小Ho笑道:“别骗我了,我们这个系列都持续这么长时间了,算法在生活中的应用场景极其有限我还是知道的。”
小Hi一副被打败的表情,又叹了一口气,道:“也是,算法就像数学一样,是能够让你知其所以然的东西,但是在实际生活中,许多问题要么太过简单,要么太过复杂,这些经典算法往往没有用武之地啊。”
看着小Hi一脸的郁闷,小Ho赶紧道:“别这样!我们还是赶紧来看今天的问题吧——既然是用线段树来解决这个问题的话,那么很容易就能想到线段树中的每一个节点维护的便是对应区间中所有商品的价值之和,这样在每次询问操作的时候,就可以使用和之前一样的方法——将询问的区间在树上分解成若干个已经计算好的区间,然后求这些区间维护的和值的和,便是我们所需要的答案。”
小Hi点了点头,道:“这部分的确和上一次的问题是一样的,但是修改操作你打算如何处理?这可就没有那么简单了!”
“这次的修改操作和之前的差别的确太大了——之前都只需要修改一个位置的值,而现在却是和询问一样,要一次性修改一个区间的值。如果仍然使用之前的方法来一个个修改的话,修改的复杂度可能会上升到O(N)呢!”小Ho忽然惊喜道:“对了,那么我就像询问一样,将修改的区间分解成若干个小区间,只修改这些区间和它们祖先结点的值不就行了么?这样的区间只会有O(logN)个,那么修改的时间复杂度也就在这个级别了!”
“你可以尝试这么做!”小Hi不怀好意的笑道。
于是小Ho回去开开心心的写了程序,但是在测试数据上折腾了很久都没有能够通过,但好在他终于发现了自己的问题所在,于是又屁颠屁颠的回来找小Hi。
“小Hi你太坏了!居然不告诉我这个问题,如果我第一次修改的是[3, 9]这个区间话,那么我就会将它拆成[3, 3], [4, 5], [6, 8], [9, 9]4个区间,那么得到修改的只有橙色的这些区间。但是如果我之后询问了[6, 7]这个区间的话,我仍然会按照修改之前的价格进行计算!”小Ho抱怨道。

“我只是说你可以尝试这么做,可没有说这么做你就能够通过的嘛~”小Hi笑道。
小Ho无奈道:“你……那现在我该怎么解决这个问题呢?”
“你再想想——其实理论上来说,如果[3, 9]这个区间被修改的话,所有绿色的结点的值都要得到重新计算的。”小Hi重新标出了一些结点。

“但是实际上是没有必要这么做的——我们可以引进一种叫做Lazy Tag,即懒惰标记的东西——的确对于[3, 9]这样一次修改操作,我可以只去修改橙色的结点,但是在这个基础上,我要在[3, 9]分解出的4个区间[3, 3], [4, 5], [6, 8], [9, 9]所对应的结点上做一个懒惰标记,表示‘之前有一次操作需要将这棵子树中的所有结点的价格都进行修改,但是因为还没有用到这棵子树中的值所以我暂时不去修改’。小Hi解释道。

“但是这些懒惰标记又有什么用呢?”小Ho问道。
“其实就是一个暂时不处理,等到需要用到的时候再进行处理的思想。”小Hi说道:“比如你之前说道的询问了[6, 7]这个区间,那么我再从上往下分解的时候,你会发现[6, 8]这个区间上有一个懒惰标记,那么你就应该进行一个懒惰标记的‘下放操作’——也就是说去修改[6, 8]这个结点的左右儿子的值,并且同时给左右儿子添加上新的懒惰标记,然后将[6, 8]的懒惰标记去掉。”
“也就是说——本来[6, 8]的左右儿子早在之前的修改操作中就需要一同进行修改的,但是因为还没有用到单独的[6, 7],[8, 8]之类的区间的原因,所以我可以暂时不处理这些结点的修改,而是用一个懒惰标记记录下来这些结点需要进行修改这件事情。然后在之后要用到这些值的时候再进行这些操作咯?”
“是的呢!”小Hi点头道:“如果你还不清楚的话,可以来看看这段伪代码:”

“嗯嗯!果然是这样,那么通过懒惰标记的作用,就可以将修改操作也降到O(logN)的复杂度了,那么这个问题就得到完美的解决了!”
于是小Ho哼着小曲,高兴的回去完善算法了~
Close
Save changes
输入
每个测试点(输入文件)有且仅有一组测试数据。每组测试数据的第1行为一个整数N,意义如前文所述。
每组测试数据的第2行为N个整数,分别描述每种商品的重量,其中第i个整数表示标号为i的商品的重量Pi。
每组测试数据的第3行为一个整数Q,表示小Hi进行的操作数。
每组测试数据的第N+4~N+Q+3行,每行分别描述一次操作,每行的开头均为一个属于0或1的数字,分别表示该行描述一个询问和一次商品的价格的更改两种情况。对于第N+i+3行,如果该行描述一个询问,则接下来为两个整数Li, Ri,表示小Hi询问的一个区间[Li, Ri];如果该行描述一次商品的价格的更改,则接下来为三个整数Li,Ri,NewP,表示标号在区间[Li, Ri]的商品的价格全部修改为NewP。
对于100%的数据,满足N<=10^5,Q<=10^5, 1<=Li<=Ri<=N,1<=Pi<=N, 0<Pi, NewP<=10^4。
输出
对于每组测试数据,对于每个小Hi的询问,按照在输入中出现的顺序,各输出一行,表示查询的结果:标号在区间[Li, Ri]中的所有商品的价格之和。样例输入
10 4733 6570 8363 7391 4511 1433 2281 187 5166 378 6 1 5 10 1577 1 1 7 3649 0 8 10 0 1 4 1 6 8 157 1 3 4 1557
样例输出
4731 14596
[code]#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int maxn=10000000;
struct tree
{
int left,right;
int value;
int lazyTag;
};
tree g[maxn];
int map[maxn];
int n;
void buildTree(int l,int r,int k)
{
g[k].left=l;
g[k].right=r;
g[k].lazyTag=-1;
if(l==r)
{
g[k].value=map[l];
return;
}
int mid=(l+r)/2;
buildTree(l,mid,k*2);
buildTree(mid+1,r,k*2+1);
g[k].value=g[2*k].value+g[k*2+1].value;
}
int search(int l,int r,int k)
{
if(g[k].left==l && g[k].right==r)
return g[k].value;
else
{
if(g[k].lazyTag!=-1)
{
g[k*2].lazyTag=g[k*2+1].lazyTag=g[k].lazyTag;
g[2*k].value=g[2*k].lazyTag*(g[2*k].right-g[2*k].left+1);
g[2*k+1].value=g[2*k+1].lazyTag*(g[2*k+1].right-g[2*k+1].left+1);
g[k].lazyTag=-1;
}
int mid=(g[k].left+g[k].right)/2;
if(r<=mid)
search(l,r,k*2);
else if(l>mid)
search(l,r,k*2+1);
else
return search(l,mid,k*2)+search(mid+1,r,k*2+1);
}
}
void change(int l,int r,int newp,int k)
{
if(l==g[k].left && r==g[k].right)
{
g[k].value=newp*(r-l+1);
g[k].lazyTag=newp;
return ;
}
else
{
if(g[k].lazyTag!=-1)
{
g[k*2].lazyTag=g[k*2+1].lazyTag=g[k].lazyTag;
// g[k].value=newp*(g[k].right-g[k].left+1); 全部覆盖的时候已经修改完了
//只需修改左右孩子
g[2*k].value=g[2*k].lazyTag*(g[2*k].right-g[2*k].left+1);
g[2*k+1].value=g[2*k+1].lazyTag*(g[2*k+1].right-g[2*k+1].left+1);
g[k].lazyTag=-1;
}
//之前在这里加了一个else改了半天
int mid=(g[k].left+g[k].right)/2;
if(r<=mid)
change(l,r,newp,2*k);
else if(l>mid)
change(l,r,newp,2*k+1);
else
{
change(l,mid,newp,2*k);
change(mid+1,r,newp,2*k+1);
}
g[k].value=g[k*2].value+g[k*2+1].value;
}
}
int main()
{
int Q,op,l,r,newp;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&map[i]);
buildTree(1,n,1);
scanf("%d",&Q);
while(Q--)
{
scanf("%d",&op);
if(op)
{
scanf("%d%d%d",&l,&r,&newp);
change(l,r,newp,1);
// for(int i=1;i<=20;i++)
// cout<<g[i].left<<" "<<g[i].right<<" "<<g[i].value<<endl;
}
else
{
scanf("%d%d",&l,&r);
printf("%d\n",search(l,r,1));
}
}
return 0;
}[/code]
相关文章推荐
- 在kali linux 上对普通用户的操作
- Py2exe打包时添加自定义库搜索目录
- Siebel_CRM
- R cannot be resolved to a variable 解决办法
- django-admin.py startproject 无法创建项目
- 2015省赛小结
- mysql的算术运算符和比较运算符
- R语言包_gbm
- ueditor样式过滤问题
- js 获取页面内容可见区域的高度和宽度
- 树状数组模版
- JAVA多线程和并发基础面试问答
- ZigZag Conversion
- 求解1-10000区间内的素数
- 对不起,我不是一个善良的人
- 揭秘AngularJS工作原理
- LeetCode -- Valid Anagram
- STL常用规则
- iOS软件版本更新思路
- SharedPreferences总结
