Lucas定理 大组合数取模
2015-08-10 13:36
429 查看
转自AC_Von
http://www.cnblogs.com/vongang/archive/2012/12/02/2798138.html
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。
这里用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence
relation holds:

where
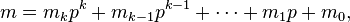
and
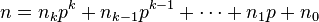
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
代码:


http://www.cnblogs.com/vongang/archive/2012/12/02/2798138.html
组合数取模 Lucas定理
对于C(n, m) mod p。这里的n,m,p(p为素数)都很大的情况。就不能再用C(n, m) = C(n - 1,m) + C(n - 1, m - 1)的公式递推了。这里用到Lusac定理
For non-negative integers m and n and a prime p, the following congruence
relation holds:

where
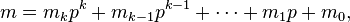
and
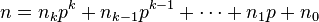
are the base p expansions of m and n respectively.
对于单独的C(ni, mi) mod p,已知C(n, m) mod p = n!/(m!(n - m)!) mod p。显然除法取模,这里要用到m!(n-m)!的逆元。
根据费马小定理:
已知(a, p) = 1,则 ap-1 ≡ 1 (mod p), 所以 a*ap-2 ≡ 1 (mod p)。
也就是 (m!(n-m)!)的逆元为 (m!(n-m)!)p-2 ;
代码:

typedef long long LL;
using namespace std;
LL exp_mod(LL a, LL b, LL p) {
LL res = 1;
while(b != 0) {
if(b&1) res = (res * a) % p;
a = (a*a) % p;
b >>= 1;
}
return res;
}
LL Comb(LL a, LL b, LL p) {
if(a < b) return 0;
if(a == b) return 1;
if(b > a - b) b = a - b;
LL ans = 1, ca = 1, cb = 1;
for(LL i = 0; i < b; ++i) {
ca = (ca * (a - i))%p;
cb = (cb * (b - i))%p;
}
ans = (ca*exp_mod(cb, p - 2, p)) % p;
return ans;
}
LL Lucas(int n, int m, int p) {
LL ans = 1;
while(n&&m&&ans) {
ans = (ans*Comb(n%p, m%p, p)) % p;
n /= p;
m /= p;
}
return ans;
}
int main() {
Read();
int n, m, p;
while(~scanf("%d%d%d", &n, &m, &p)) {
printf("%lld\n", Lucas(n, m, p));
}
return 0;
}
相关文章推荐
- 修改HTML5 input placeholder默认颜色
- 将pdf转换成html的方法
- 阿里巴巴2014校招笔试题-2013年9月14日
- 常用字符串Hash函数
- 矩阵hash + KMP - UVA 12886 The Big Painting
- 数据库事务操作+数据库事务隔离级别
- iOS 多线程
- 从网络上下载文件到本地
- select()函数以及FD_ZERO、FD_SET、FD_CLR、FD_ISSET
- SparkException: Failed to get broadcast (TorrentBroadcast)
- leetcode 111 —— Minimum Depth of Binary Tree
- wcf中的File-less Activation
- poj 2774
- postgresql数据库psql控制台操作命令
- construct express
- jquery 回车事件
- Hive表数据导入到Hbase
- 利用双缓冲消除图片重画的闪烁现象
- leetCode #232 Implement Queue using Stacks
- python生成随机用户名及密码方法
