hiho一下 连通性·四 点的双连通分量
2015-07-25 00:02
483 查看
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
小Hi和小Ho从约翰家回到学校时,网络所的老师又找到了小Hi和小Ho。
老师告诉小Hi和小Ho:之前的分组出了点问题,当服务器(上次是连接)发生宕机的时候,在同一组的服务器有可能连接不上,所以他们希望重新进行一次分组。这一次老师希望对连接进行分组,并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。
这一次的条件是对于同一个组满足:当组内任意一个服务器宕机之后,不会影响组内其他服务器的连通性。在满足以上条件下,每个组内的边数量越多越好。
比如下面这个例子,一共有6个服务器和7条连接:

其中包含3个组,分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言,和该组边相关联的有{1,2,3}三个服务器:当1宕机后,仍然有2-3可以连接2和3;当2宕机后,仍然有1-3可以连接1和3;当3宕机后,仍然有1-2可以连接1和2。
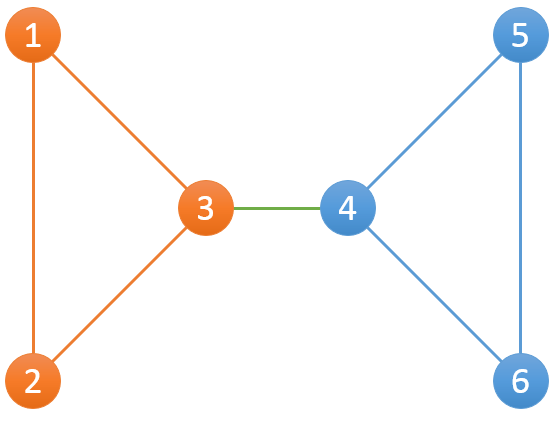
老师把整个网络的情况告诉了小Hi和小Ho,希望小Hi和小Ho统计一下一共有多少个分组。
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000
第2..M+1行:2个正整数,u,v。第i+1行表示存在一条边(u,v),编号为i,连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
第1行:1个整数,表示该网络的连接组数。
第2行:M个整数,第i个数表示第i条连接所属组内,编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]},方括号内表示编号,则输出{1,1,1,4,5,5,5}。
样例输入
样例输出
小Ho:那么我们这一次求的和前一次有什么区别?
小Hi:在上一次中,我们求解的是边的双连通分量,而我们这一次叫做点的双连通分量,其定义为:
对于一个无向图的子图,当删除其中任意一个点后,不改变图内点的连通性,这样的子图叫做点的双连通子图。而当子图的边数达到最大时,叫做点的双连通分量。
小Ho:那和上一次有什么不同么?
小Hi:与前一次的区别在于,可能出现下面这种情况时:
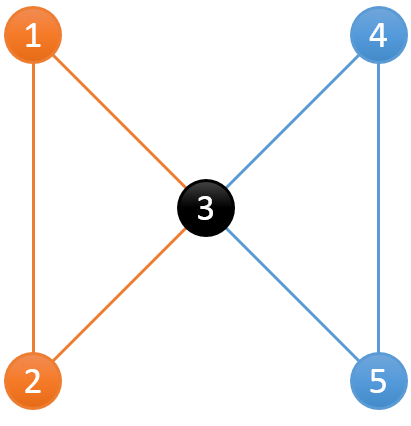
存在两个分组,分别是{(1,2),(2,3),(3,1)},{(3,4),(4,5),(3,5)}。其不能分成一组是因为当3号服务器宕机之后,1,2与4,5便不再连通。
小Ho:感觉好像难了很多?
小Hi:其实也还好啦,这一次的话只需要稍作一下改进就好。
首先我们从上面的例子可以猜到,桥一定是作为一个单独的点的双连通分量。而被桥分割的区域,可能出现两种情况:
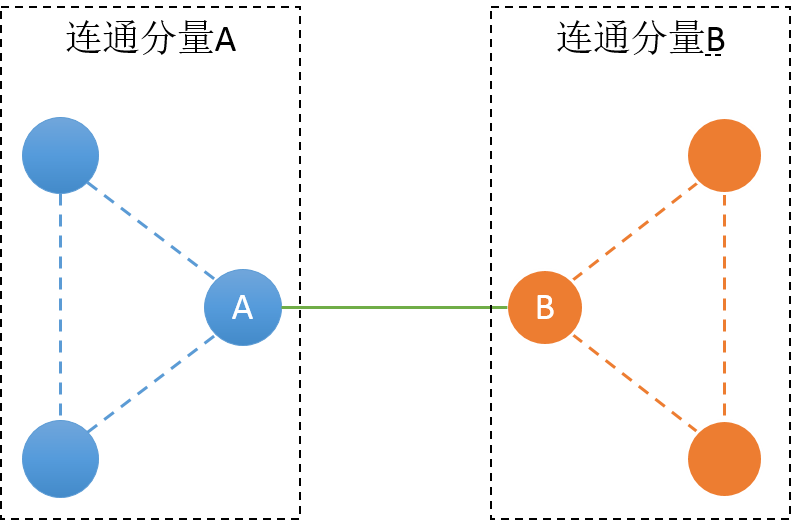
第一种情况下,桥两边都各是一个连通分量,那么桥的存在把整个图分成了3个连通分量,桥本身作为一个点的双连通分量,而A,B两个分量还无法判定。在这图中,A,B两点本质都是割点。
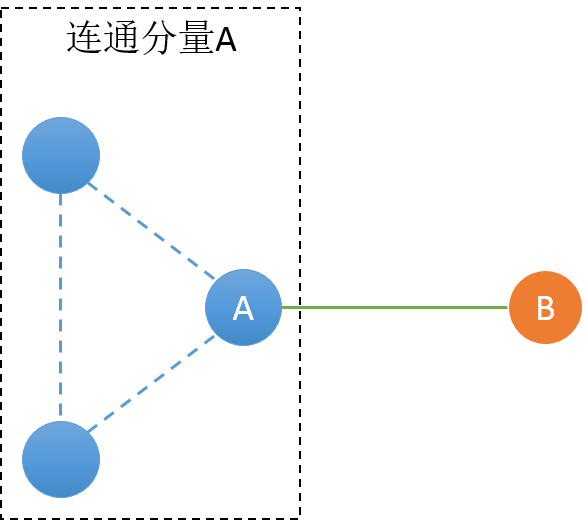
第一种情况下,桥一边是连通分量,而另一边是独立的点。桥的存在把整个图分成了2个连通分量,B点部分因为没有边,所以不构成一个组。在这图中,只有A点是割点。
那么我们可以先根据桥,把整个图先分割开来。
在点的双连通分量分量中出现了一种特殊的情况,而产生这种情况是因为在一个边的双连通分量中存在了割点。那么在去掉桥的每一个连通分量中,我们需要再找出割点。
小Ho:简单每存在一个桥就分割一次图,每个连通分量中存在一个割点就分割一次图。
小Hi:是这样的,但其实还可以更近一步考虑,对于桥的两种情况,它分割个区域数刚好就等于割点数+1;而连通分量内的割点同样也是,每存在一个割点,点的双连通分量就增加一个。
小Ho:这样说来,只要统计割点数量,点的双连通分量就等于割点数量加1咯?
小Hi:没错,每存在一个割点,就把一个区域一分为二,所以最后的结果也就是统计割点的数量就可以了。而对于分组具体情况,我们仍然采用栈来辅助我们记录,代码如下(注:官方提示代码有误):
AC代码:
其实限制条件可以这样改:
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho从约翰家回到学校时,网络所的老师又找到了小Hi和小Ho。老师告诉小Hi和小Ho:之前的分组出了点问题,当服务器(上次是连接)发生宕机的时候,在同一组的服务器有可能连接不上,所以他们希望重新进行一次分组。这一次老师希望对连接进行分组,并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。
这一次的条件是对于同一个组满足:当组内任意一个服务器宕机之后,不会影响组内其他服务器的连通性。在满足以上条件下,每个组内的边数量越多越好。
比如下面这个例子,一共有6个服务器和7条连接:

其中包含3个组,分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言,和该组边相关联的有{1,2,3}三个服务器:当1宕机后,仍然有2-3可以连接2和3;当2宕机后,仍然有1-3可以连接1和3;当3宕机后,仍然有1-2可以连接1和2。

老师把整个网络的情况告诉了小Hi和小Ho,希望小Hi和小Ho统计一下一共有多少个分组。
输入
第1行:2个正整数,N,M。表示点的数量N,边的数量M。1≤N≤20,000, 1≤M≤100,000第2..M+1行:2个正整数,u,v。第i+1行表示存在一条边(u,v),编号为i,连接了u,v两台服务器。1≤u<v≤N
保证输入所有点之间至少有一条连通路径。
输出
第1行:1个整数,表示该网络的连接组数。第2行:M个整数,第i个数表示第i条连接所属组内,编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]},方括号内表示编号,则输出{1,1,1,4,5,5,5}。
样例输入
6 7 1 2 1 3 2 3 3 4 4 5 4 6 5 6
样例输出
3 1 1 1 4 5 5 5
提示:点的双连通分量
小Ho:那么我们这一次求的和前一次有什么区别?小Hi:在上一次中,我们求解的是边的双连通分量,而我们这一次叫做点的双连通分量,其定义为:
对于一个无向图的子图,当删除其中任意一个点后,不改变图内点的连通性,这样的子图叫做点的双连通子图。而当子图的边数达到最大时,叫做点的双连通分量。
小Ho:那和上一次有什么不同么?
小Hi:与前一次的区别在于,可能出现下面这种情况时:

存在两个分组,分别是{(1,2),(2,3),(3,1)},{(3,4),(4,5),(3,5)}。其不能分成一组是因为当3号服务器宕机之后,1,2与4,5便不再连通。
小Ho:感觉好像难了很多?
小Hi:其实也还好啦,这一次的话只需要稍作一下改进就好。
首先我们从上面的例子可以猜到,桥一定是作为一个单独的点的双连通分量。而被桥分割的区域,可能出现两种情况:

第一种情况下,桥两边都各是一个连通分量,那么桥的存在把整个图分成了3个连通分量,桥本身作为一个点的双连通分量,而A,B两个分量还无法判定。在这图中,A,B两点本质都是割点。

第一种情况下,桥一边是连通分量,而另一边是独立的点。桥的存在把整个图分成了2个连通分量,B点部分因为没有边,所以不构成一个组。在这图中,只有A点是割点。
那么我们可以先根据桥,把整个图先分割开来。
在点的双连通分量分量中出现了一种特殊的情况,而产生这种情况是因为在一个边的双连通分量中存在了割点。那么在去掉桥的每一个连通分量中,我们需要再找出割点。
小Ho:简单每存在一个桥就分割一次图,每个连通分量中存在一个割点就分割一次图。
小Hi:是这样的,但其实还可以更近一步考虑,对于桥的两种情况,它分割个区域数刚好就等于割点数+1;而连通分量内的割点同样也是,每存在一个割点,点的双连通分量就增加一个。
小Ho:这样说来,只要统计割点数量,点的双连通分量就等于割点数量加1咯?
小Hi:没错,每存在一个割点,就把一个区域一分为二,所以最后的结果也就是统计割点的数量就可以了。而对于分组具体情况,我们仍然采用栈来辅助我们记录,代码如下(注:官方提示代码有误):
void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;
//记录节点u的子树数
int children = 0;
ArcNode *p = graph[u].firstArc;
visit[u] = 1;
//初始化dfn与low
dfn[u] = low[u] = ++counter;
for(; p != NULL; p = p->next) {
int v = p->adjvex;
if(edge(u,v)已经被标记) continue; // 修改 1
//节点v未被访问,则(u,v)为树边
if(!visit[v]) {
children++;
parent[v] = u;
edgeStack[top++] = edge(u,v); // 将边入栈 // 修改 2
dfs(v);
low[u] = min(low[u], low[v]);
//case (1)
if(parent[u] == NIL && children > 1) {
printf("articulation point: %d\n", u);
// mark edge
// 将边出栈,直到当前边出栈为止,这些边标记为同一个组
do {
nowEdge = edgeStack[top];
top--;
// 标记nowEdge
} while (nowEdge != edge(u,v))
}
//case (2)
if(parent[u] != NIL && low[v] >= dfn[u]) {
printf("articulation point: %d\n", u);
// mark edge
// 将边出栈,直到当前边出栈为止,这些边标记为同一个组
do {
nowEdge = edgeStack[top];
top--;
// 标记nowEdge
} while (nowEdge != edge(u,v))
}
}
//节点v已访问,则(u,v)为回边
else if(v != parent[u]) {
edgeStack[top++] = edge(u,v); // 将边入栈 // 修改 3
low[u] = min(low[u], dfn[v]);
}
}
}AC代码:
#include <iostream>
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
#include <queue>
#include <algorithm>
using namespace std;
#define maxn 20100
#define maxe 200100
struct edge
{
int u,v,id;
int next;
}Edge[maxe];
int dfn[maxn],low[maxn],head[maxe],belong[maxe],parent[maxn],Min[maxe],Stack[maxe],n,m,cnt,Counter,top,ans;
void AddEdge(int a,int b,edge *Edge,int *head,int ID)
{
Edge[cnt].u=a;
Edge[cnt].v=b;
Edge[cnt].id=ID;
Edge[cnt].next=head[a];
head[a]=cnt++;
}
void dfs(int u)
{
int v,children=0;
dfn[u]=low[u]=++Counter; // 为节点u设定次序编号和Low初值
for (int i=head[u]; i!=-1; i=Edge[i].next) // 枚举每一条边
{
v=Edge[i].v;
if(belong[Edge[i].id]!=-1)
{
continue;
}
if(!dfn[v]) // 如果节点v未被访问过
{
children++;
parent[v]=u;
Stack[++top]=Edge[i].id;
dfs(v); // 继续向下找
low[u]=min(low[u],low[v]);
if(( low[v]>=dfn[u] && parent[u]!=-1)|| (parent[u]==-1 && children>1)) //割点充要条件
{
ans++;
int min=100000000;
int k;
do
{
k=Stack[top--];
belong[k]=ans; //该边所属分组
if(k<min)
{
min=k;
}
}while(k!=Edge[i].id);
Min[ans]=min; //该组最小连接编号
}
}
else if(v!=parent[u]) //回边(v是u的祖先结点)
{
Stack[++top]=Edge[i].id;
low[u]=min(low[u],dfn[v]);
}
}
}
void Init() //初始化
{
cnt=0;
Counter=0;
ans=0;
top=-1;
memset(head, -1, sizeof(head));
for (int i=0; i<=n; i++)
{
dfn[i]=0;
parent[i]=-1;
}
for (int i=0; i<=m; i++)
{
Min[i]=1;
belong[i]=-1;
}
}
int main()
{
int u,v;
scanf("%d%d",&n,&m);
Init();
for (int i=1; i<=m; i++)
{
scanf("%d%d",&u,&v);
AddEdge(u,v,Edge,head,i);
AddEdge(v,u,Edge,head,i);
}
dfs(1);
int k,min=100000000;
ans++;
while (top!=-1) //栈未空,继续处理
{
k=Stack[top--];
belong[k]=ans; //该边所属分组
if(k<min)
{
min=k;
}
}
Min[ans]=min;
printf("%d\n",ans);
for (int i=1; i<=m; i++)
{
printf("%d ",Min[belong[i]]);
}
return 0;
}其实限制条件可以这样改:
if(low[v]>=dfn[u]) //割点充要条件这样退出dfs后,栈就为空了,不用在单独处理一组数据了。
相关文章推荐
- Linuxc 文件操作讲座知识
- linux程序设计——套接字选项(第十五章)
- 以实例简介Java中线程池的工作特点
- java多线程学习笔记——concurrent包的一些类(Lock 和Condition)
- Windows 2008 R2 64bit Apache 2.4.4 + PHP 5.5.27 配置
- 小贝_mysql分区理论学习
- 使用 IBM Bluemix 构建,部署和管理自定义应用程序
- 使用纯php代码实现页面伪静态的方法
- php实现QQ空间获取当前用户的用户名并生成图片
- Python实现将DOC文档转换为PDF的方法
- Python实现的RSS阅读器实例
- Python导出DBF文件到Excel的方法
- Python自动扫雷实现方法
- Python实现对excel文件列表值进行统计的方法
- Python基于PycURL实现POST的方法
- Python基于PycURL自动处理cookie的方法
- Python实现截屏的函数
- Python实现简单的代理服务器
- Python基于有道实现英汉字典功能
- Python实现模拟登录及表单提交的方法
