暑假NOIP笔记—数论

数论小结

今天上午数论，下午组合数学，and第一天。

上午主要讲了7点

- 取模

- 快速幂

- 快筛素数

- 分解质因数

- 约数个数(和)

- 欧拉函数

- 欧拉定理以及费马小定理

取模

加法

(A+B) mod C = (A mod C + B mod C) mod C

减法

(A-B) mod C = (A mod C - B mod C) mod C

乘法

(A * B) mod  C = (A mod C) * (B mod C) mod C

特殊强调的是对于减法取模要通过加减若干个MOD 来使ans在0~MOD-1的范围内。

※ A%B=A-(A/B)*B

取模的应用

Quickpow(快速幂) 用到了二进制拆分的思想，比如说13=（1101）2，那么a^13=a*a^4*a^8，可以利用这种思想来求解 a^b %p 的问题

int Quick_pow(int x,int y)
{
int ans=1;
x%=MOD;
while(y)
{
if(y%2==1)
{
ans=(ans*x)%MOD;
}
y/=2;
x=(x*x)%MOD;
}
return ans;
}

EX：

等比数列和取模

(1+a+a^2+a^3+…+a^b)%p 1<=a, b, p <= 10^9

同样，可以用二进制拆分的方法：

二进制拆解	乘a^x
1	a
1+a	a^2
1+a+a^2+a^3	a^4
…	…
1+a+a^2+a^3+…+a^（2^k-1）	a^(2^k)

把左面看作一个整体，再上右面找到一个相乘，这样就可以得到a+a^2+…a^x的和了，剩下的暴力算就好了。

快筛素数

#include<stdio.h>
bool book[50001001];
int prime[5000000];
int cnt;
void pre_init(long long n)
{
for(int i=2;i<=n;i++)
{
if(book[i]==0)
{
prime[cnt++]=i;
}
for(int j=0;j<cnt&&i*prime[j]<=n;j++)
{
book[i*prime[j]]=1;
if(i%prime[j]==0)
{
break;
}
}
}
}

筛素数的算法很重要，时间复杂度计算如下：

筛的次数近似为n * lnln N

所以算法复杂度为O(n loglog N)

在sqrt(N)内，为sqrt(N/(lnN))

用线性筛法同样可以筛欧拉，以及其他的一些积性函数，在后面会有提及。

分解质因数

一个数最多只有一个大于sqrt(P)的质因子。

依次试除1..sqrt(P)即可。

优化：只试除质数

Bettter solution: Pollard’s Rho (据说没什么用)

约数个数（和）

如果有一个sqrt(N)…N内的约数，则必有一在1…sqrt(N)内的约数与之对应

枚举1…sqrt(N)内的所有数即可

long long f(long long n)
{
long long ret=1;
for(long long i=2;i*i<=n;i++)
{
long long cnt=0;
while(n%i==0)
{
cnt++;
n/=i;
}
ret*=(cnt+1);
}
if(n!=1)
{
ret=ret*2;
}
return ret;
}

设d(x)为x的约数个数，求d(1)+d(2)+d(3)+…+d(n)

其实很简单了，for(int i=1;i<=n;i++) sum+=(x/i);

这里的(x/i)表示有这些个数有约数i

在这里引申一个概念 “调和级数”

名称定义：

很早就有数学家研究，比如中世纪后期的数学家Oresme在1360年就证明了这个级数是发散的。他的方法很简单：

1 +1/2+1/3 +1/4 + 1/5+ 1/6+1/7+1/8 +…

1/2+1/2+(1/4+1/4)+(1/8+1/8+1/8+1/8)+…

注意后一个级数每一项对应的分数都小于调和级数中每一项，而且后面级数的括号中的数值和都为1/2，这样的1/2有无穷多个，所以后一个级数是趋向无穷大的，进而调和级数也是发散的。

从更广泛的意义上讲,如果An是全部不为0的等差数列，则1/An就称为调和数列，求和所得即为调和级数，易得，所有调和级数都是发散于无穷的。 —— [ 百度百科 ]

1 +1/2+1/3 +1/4 + 1/5+ 1/6+1/7+1/8 +…+1/n =ln(n+1)+r；

r为一个常数约等于0.5772156649

欧拉函数

主要强调一下 欧拉函数 是一个积性函数 ，

若m,n互质，φ(mn)=φ(m)φ(n)

通常可以用一下方法实现：

long long Euler(long long n)
{
long long num=n;
for(long long i=2;i*i<=num;i++)
{
if(n%i==0)
{
num=(num/i)*(i-1);
while(n%i==0)
{
n/=i;
}
}
}
if(n>1)
{
num=num/n*(n-1);
}
return num;
}

但是，就像之前说过的，我们可以在快筛素数的同时，进行快筛欧拉

void pre_init(ll n)
{
phi[1]=1;
for(ll i=2;i<=n;i++)
{
if(book[i]==0)
{
prime[cnt++]=i;
phi[i]=i-1;
}
for(ll j=0;j<cnt&&i*prime[j]<=n;j++)
{
book[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else
{
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
}

BZOJ2818就是典型的题目，类似的，Visible Lattice Points同样如此。

#include<stdio.h>
#include<string.h>
#define MAXN 1000000
typedef long long ll;
ll cnt,n;
ll prime[MAXN],book[MAXN],phi[MAXN],f[MAXN];
void pre_init(ll n)
{
phi[1]=1;
for(ll i=2;i<=n;i++)
{
if(book[i]==0)
{
prime[cnt++]=i;
phi[i]=i-1;
}
for(ll j=0;j<cnt&&i*prime[j]<=n;j++)
{
book[i*prime[j]]=1;
if(i%prime[j]==0)
{
phi[i*prime[j]]=phi[i]*prime[j];
break;
}
else
{
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
}
int main()
{
while(~scanf("%lld",&n))
{
pre_init(n);
ll sum=0;
for(ll i=1;i<=n;i++)
{
sum+=phi[i];
}
printf("%lld\n",sum*2+1);
}
return 0;
}

同样，也可以用类似的方法筛逆元，需要强调的是 逆元 具有完全积性 也就是说f(ab)=f(a)f(b)且a,b不需要互质。

欧拉定理&费马小定理

略

Afternoon:

下午的很多知识都是建立在上午的基础上，主要有以下的几方面：

- 欧几里得算法及扩展

- 中国剩余定理

- 组合数取模

- 余数之和

- 高斯消元

- 其它

First，引出一道很有趣的题目【bzoj2721】[Violet 5]樱花

意为 1/x+1/y=1/(n!) [给定n]求解的个数

Solution：

设z=n! => xz+yz=xy => x=yz/(y-z) =>(1+z/(y-z))*z

=>z+(z)^2/(y-z)

所以就转化为了求z的约数个数，也就是n!的约数个数了。

欧几里得算法

欧几里得算法又名“辗转相除法”，还是觉得 辗转相除法 这个 名字更揭示了本质。欧几里得算法 是用于求a,b两个数的最大公约数

Gcd(a,b)=Gcd(b,a mod b)

像其他的算法定理一样，我们不需要知道它是怎么来的 ，会用就好。

如：

4,6 -> 2,4 ==> 2

3,8 -> 2,3 -> 1,2 ==> 1

2,9 -> 1,2 ==> 1

Ex:

欧几里得算法的扩展应用是求不定方程的解 ax+by=d ，显然，当d%( lcm(a,b) )为真时才有解，这是其必要条件。

下面来看 推导过程：

先由特殊到一般，当d=gcd(a,b)时：

ax + by =d => bx + (a - a / b * b)y d =>ay +b(x - a / b*y) =d

这样 就又化成了 ax+by 的形式，只不过x=y ; y=(x - a / b*y)

Sumarry：

已知a,b求接一组p,q，令 pa+qb=Gcd(p,q)[解一定存在]

And,若要求ax+by=c(c不需要特殊),即在每个解上乘上 c/Gcd(p,q)

若(x0,y0)为一组解，则所有解 x=x0+bt ; y=y0-at ,n∈N*

long long Exgcd(long long a,long long b)
{
if(b==0)
{
x=1;
y=0;
ret=a;
}
else
{
ret=Exgcd(b,a%b);
long long t=x;
x=y;
y=t-a/b*x;
}
return ret;
}

中国剩余定理

中国剩余定理又名 孙子定理，中国古代求解一次同余式组（见同余）的方法。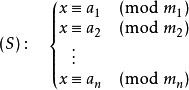



了解孙子定理，一定要知道“构造法”，也是求解的重要思想。

证明如下：



a≡b(mod m) 是个很重要的概念，虽说这个很基础，但是必须要强调一下 ，因为如果这个 不十分清晰那么对于后续的做题会造成很大的困扰。

a≡b(mod m) 读作a与b对模m同余 即(a-b)/m为整数

经典题目：VIJOS P1164曹冲养猪

#include<stdio.h>
#define max 1000
long long a[max+1];
long long b[max+1];
long long ret;
long long x=1,y=0;
void Exgcd(long long a,long long b)
{
if(b==0)
{
x=1;
y=0;
}
else
{
Exgcd(b,a%b);
long long t=x;
x=y;
y=t-a/b*x;
}
}
long long remider(long long *a,long long *b,long long ilen)
{
long long i,n=1;
for(i=0;i<ilen;i++)
{
n*=a[i];
}
for(i=0;i<ilen;i++)
{
long long m=n/a[i];
x=1,y=0;
Exgcd(m,a[i]);
x=(x%a[i]+a[i])%a[i];
ret=(ret+m*b[i]*x%n)%n;
}
return ret;
}
int main()
{
long long ilen;
scanf("%lld",&ilen);
for(int i=0;i<ilen;i++)
{
scanf("%lld%lld",&a[i],&b[i]);
}
printf("%lld",remider(a,b,ilen));
return 0;
}

组合数取模

组合数取模的应用之一就是所谓的二项式展开系数

（a+b)^n=a^n + a^（n-1）b + a^（n-2） b^2 + a^（n-3）*b^3 + …….+a^3 b^（n-3） + a^2 b^（n-2）+ a b^（n-1） + b^n



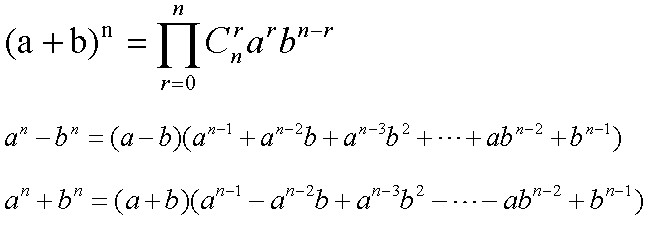
组合数取模的其它知识之前也有转载过相关文章，自我觉得还是相当好的，在这里就 不赘述了

http://blog.csdn.net/z_mendez/article/details/46593827

余数之和

明确 A%B=A-(A/B)*B,就好了 ~

#include<stdio.h>
#include<string.h>
#define MANX 1000000000
typedef long long ll;
ll n,k;
ll min(ll a,ll b){return a<b?a:b;}
int main()
{
scanf("%lld%lld",&n,&k);
ll ans=n*k,sub=0;
for(ll i=1;i<=min(n,k);i++)
{
ll a=k/i,b=k/a;
b=min(b,n);
sub+=a*(i+b)*(b-i+1)/2;
i=b;
}
printf("%lld\n",ans-sub);
return 0;
}

其它

高斯消元

题目List：

- BZOJ2721 樱花

- BZOJ 2818 GCD

- BZOJ 2142 礼物

- BZOJ1406 密码箱

- BZOJ 1257 余数之和

- BZOJ2186 沙拉公主的困惑

- NOIP 2009 Hankson的趣味题