奇异值分解
2015-07-16 19:53
204 查看
参考资料:
1)A Tutorial on Principal Component Analysis, Jonathon Shlens
这是我关于用SVD去做PCA的主要参考资料
2)http://www.ams.org/samplings/feature-column/fcarc-svd
关于svd的一篇概念好文,我开头的几个图就是从这儿截取的
3)http://www.puffinwarellc.com/index.php/news-and-articles/articles/30-singular-value-decomposition-tutorial.html
另一篇关于svd的入门好文
4)http://www.puffinwarellc.com/index.php/news-and-articles/articles/33-latent-semantic-analysis-tutorial.html
svd与LSI的好文,我后面LSI中例子就是来自此
5)http://www.miislita.com/information-retrieval-tutorial/svd-lsi-tutorial-1-understanding.html
另一篇svd与LSI的文章,也还是不错,深一点,也比较长
6)Singular Value Decomposition and Principal Component Analysis, Rasmus Elsborg Madsen, Lars Kai Hansen and Ole Winther, 2004
一、SVD奇异值分解概念
在多数情况下,数据中的一小段携带了数据集中的大部分信息,其他信息要么是噪声,要么就是毫不相干的信息。在线性代数中有很多矩阵分解技术,通过它们可以将原始矩阵表示成新的易于处理的形式。不同的矩阵分解技术具有不同的性质,有各自特定的应用场景。
奇异值分解SVD作为矩阵分解的一种类型,可以使我们只用很小的数据集就能表达原始数据集,它可以从噪声数据中抽取特征值。SVD可以将任意维数的原始数据集矩阵Data分解成三个矩阵U、Σ、VT,如下公式所示:
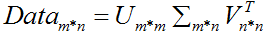
特征值:
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:

这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
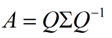
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。我这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:

它其实对应的线性变换是下面的形式:
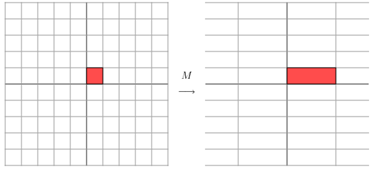
因为这个矩阵M乘以一个向量(x,y)的结果是:
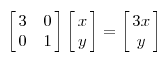
上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:

它所描述的变换是下面的样子:
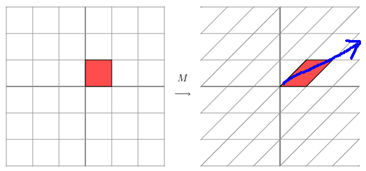
上述分解中会构建出一个矩阵Σ,该矩阵只有对角元素,其他元素均为0.此外,Σ的对角元素是从大到小排列的,这些对角线元素称为原始数据集矩阵Data的“奇异值”singular value。它与PCA特征的联系:PCA得到的是矩阵的特征值,奇异值就是矩阵Data*DataT特征值的平方根。

设A∈Rrm*n,ATA的特征值为:
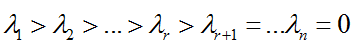
则称
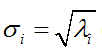
(i=1,2,…,n)为矩阵A的奇异值。
当A为零矩阵时,它的所有奇异值均为零。一般的,矩阵A的奇异值个数等于A的列数,A的非零奇异值的个数等于A的秩。
接下来,首先用数学推导介绍SVD存在的必然性。
一些定义:
正交矩阵:
如果方正Q满足QTQ=QQT=I(或者等价的Q-1=QT),则称Q为正交矩阵。
非奇异矩阵:
若n阶矩阵A的行列式不为零,即 |A|≠0,则称A为非奇异矩阵或满秩矩阵,否则称A为奇异矩阵或降秩矩阵。
正定矩阵:
设M是n阶方阵,如果对任何非零向量z,都有 zTMz > 0,就称M正定矩阵。
定理证明:
定理1 (实对称矩阵正交相似于对角矩阵):
对任意n阶实对称矩阵A,都有n阶正交矩阵Q,使得

为了证明该定理,首先给出并证明两个引理:
. 实对称矩阵特征值为实数
若任意n阶矩阵的特征值为实数,则有正交矩阵Q,使得

引理1,证明:
设λ为A的一个特征值,x为对应的特征向量,则有Ax = λx,因此
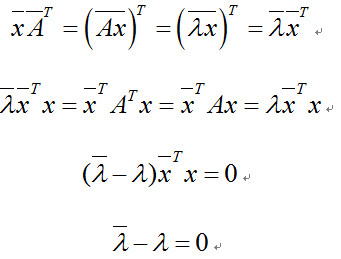
所以特征值必为实数。
引理2,利用数学归纳法证明:
当n=1时,结论显然成立
设对n-1阶矩阵的结论也成立,现在证明对n阶矩阵结论依然成立
令λ1为A的一个实特征值,相应的特征向量为a1,不妨设a1已单位化。把a1扩充为Rn的标准正交基a1, a2,…, an,构造矩阵X=(a2,…, an)和P=(a1,X),则P为正交矩阵且有:
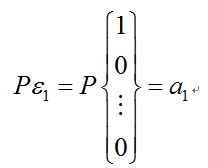
于是,AP = (Aa1, AX)= (λ1a1, P(P-1AX)) = (λ1Pε1,P(P-1AX)) = P(λ1ε1, P-1AX)。设:

【个人理解:A->n*n,X->n*n-1,P->n*n,则P-1AX->n*n-1,正好这么拆,a’->1*n-1】
从而有:
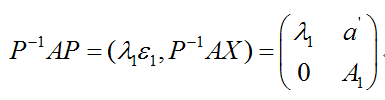
根据归纳假设,对于A1有n-1阶正交矩阵T,使得T-1A1T = TTA1T= At为上三角矩阵,现取:
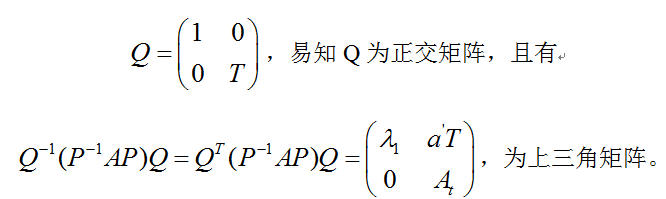
由于P和Q都是正交矩阵,而正交矩阵相乘结果R仍是正交矩阵,因此可以写作:
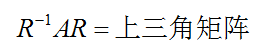
现在回到定理1的证明,因为A为实对称矩阵,则有引理1知,A的特征值均为实数。由引理2知,存在正交矩阵R,使得
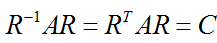
C为上三角矩阵,而A=AT,则有C=CT,但C是上三角矩阵,CT为下三角矩阵,所以C必为对角矩阵。定理1得证。其中,C的对角线元素即为A的特征值构成。
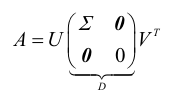
其中,Σ = diag(σ1,σ2,…, σr),即σ1, σ2,…,σr是A的非零奇异值,亦记作A=UDVT
证明:
记对称矩阵ATA的特征值为:
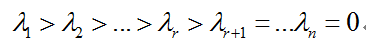
由对称矩阵的正交分解(定理1),我们有:
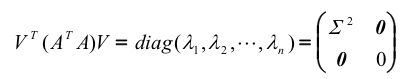
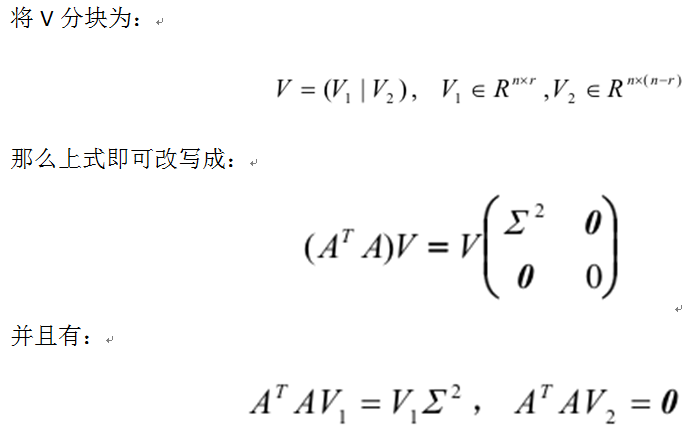
由第一个公式可以得到,
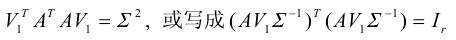
由第二个公式可以得到,
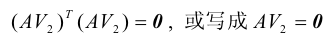

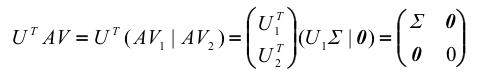
故有
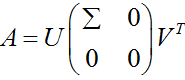
,证毕
若记U=(u1, u2,…,um),V=(v1, v2,…,vn),根据SVD的分解,A可以表示为:
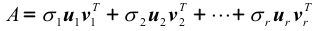
上式就是A的奇异值分解过程。
二、SVD奇异值分解求解及实现
上面的一堆推导,只是为了说明对任意矩阵都存在奇异值分解,而没有讲述如何求解奇异值分解。以下内容来自《徐士良C常用算法程序集(第二版)》,一般实矩阵的奇异值分解:
用household变换和变形QR算法对一般实矩阵进行奇异值分解,得到左右奇异向量U、V及奇异值矩阵D。
[个人认为具体怎么求SVD,大家不要去记和理解了,要用的时候能找到源码,方便其他移植即可]
例:求下面两个矩阵A和B的奇异值分解,ε取0.000001

三、SVD应用实例
1. 基于SVD的图像压缩
这个例子比较简单,首先进行奇异值分解,得到奇异值矩阵,和左右奇异向量。然后由于只要很少的奇异值,就能包含绝大部分被分解的矩阵信息,因此我们挑选不同数量的奇异值,重构图像,比较差异。这边分别实现了灰度图、RGB三色图的SVD分解。【奇异值到底选多少,自己打印奇异值矩阵,从大到小排序的,小到什么程度就舍弃,实际情况实际操作。。。】
结果:


效果图:


注意:SVD压缩只是为了存储更少的数据来表达原始图像,在重构图像时,奇异值矩阵仍旧是要和原始图像大小一样的,只不过大部分地方用0填充罢了。
1)A Tutorial on Principal Component Analysis, Jonathon Shlens
这是我关于用SVD去做PCA的主要参考资料
2)http://www.ams.org/samplings/feature-column/fcarc-svd
关于svd的一篇概念好文,我开头的几个图就是从这儿截取的
3)http://www.puffinwarellc.com/index.php/news-and-articles/articles/30-singular-value-decomposition-tutorial.html
另一篇关于svd的入门好文
4)http://www.puffinwarellc.com/index.php/news-and-articles/articles/33-latent-semantic-analysis-tutorial.html
svd与LSI的好文,我后面LSI中例子就是来自此
5)http://www.miislita.com/information-retrieval-tutorial/svd-lsi-tutorial-1-understanding.html
另一篇svd与LSI的文章,也还是不错,深一点,也比较长
6)Singular Value Decomposition and Principal Component Analysis, Rasmus Elsborg Madsen, Lars Kai Hansen and Ole Winther, 2004
一、SVD奇异值分解概念
在多数情况下,数据中的一小段携带了数据集中的大部分信息,其他信息要么是噪声,要么就是毫不相干的信息。在线性代数中有很多矩阵分解技术,通过它们可以将原始矩阵表示成新的易于处理的形式。不同的矩阵分解技术具有不同的性质,有各自特定的应用场景。
奇异值分解SVD作为矩阵分解的一种类型,可以使我们只用很小的数据集就能表达原始数据集,它可以从噪声数据中抽取特征值。SVD可以将任意维数的原始数据集矩阵Data分解成三个矩阵U、Σ、VT,如下公式所示:
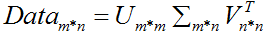
特征值:
如果说一个向量v是方阵A的特征向量,将一定可以表示成下面的形式:

这时候λ就被称为特征向量v对应的特征值,一个矩阵的一组特征向量是一组正交向量。特征值分解是将一个矩阵分解成下面的形式:
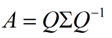
其中Q是这个矩阵A的特征向量组成的矩阵,Σ是一个对角阵,每一个对角线上的元素就是一个特征值。我这里引用了一些参考文献中的内容来说明一下。首先,要明确的是,一个矩阵其实就是一个线性变换,因为一个矩阵乘以一个向量后得到的向量,其实就相当于将这个向量进行了线性变换。比如说下面的一个矩阵:

它其实对应的线性变换是下面的形式:

因为这个矩阵M乘以一个向量(x,y)的结果是:
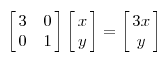
上面的矩阵是对称的,所以这个变换是一个对x,y轴的方向一个拉伸变换(每一个对角线上的元素将会对一个维度进行拉伸变换,当值>1时,是拉长,当值<1时时缩短),当矩阵不是对称的时候,假如说矩阵是下面的样子:

它所描述的变换是下面的样子:

上述分解中会构建出一个矩阵Σ,该矩阵只有对角元素,其他元素均为0.此外,Σ的对角元素是从大到小排列的,这些对角线元素称为原始数据集矩阵Data的“奇异值”singular value。它与PCA特征的联系:PCA得到的是矩阵的特征值,奇异值就是矩阵Data*DataT特征值的平方根。

设A∈Rrm*n,ATA的特征值为:
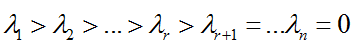
则称
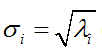
(i=1,2,…,n)为矩阵A的奇异值。
当A为零矩阵时,它的所有奇异值均为零。一般的,矩阵A的奇异值个数等于A的列数,A的非零奇异值的个数等于A的秩。
接下来,首先用数学推导介绍SVD存在的必然性。
一些定义:
正交矩阵:
如果方正Q满足QTQ=QQT=I(或者等价的Q-1=QT),则称Q为正交矩阵。
非奇异矩阵:
若n阶矩阵A的行列式不为零,即 |A|≠0,则称A为非奇异矩阵或满秩矩阵,否则称A为奇异矩阵或降秩矩阵。
正定矩阵:
设M是n阶方阵,如果对任何非零向量z,都有 zTMz > 0,就称M正定矩阵。
定理证明:
定理1 (实对称矩阵正交相似于对角矩阵):
对任意n阶实对称矩阵A,都有n阶正交矩阵Q,使得

为了证明该定理,首先给出并证明两个引理:
. 实对称矩阵特征值为实数
若任意n阶矩阵的特征值为实数,则有正交矩阵Q,使得

引理1,证明:
设λ为A的一个特征值,x为对应的特征向量,则有Ax = λx,因此
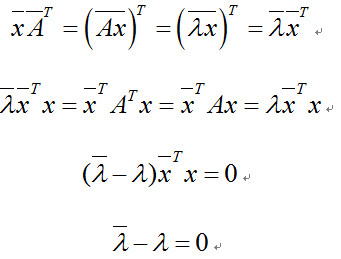
所以特征值必为实数。
引理2,利用数学归纳法证明:
当n=1时,结论显然成立
设对n-1阶矩阵的结论也成立,现在证明对n阶矩阵结论依然成立
令λ1为A的一个实特征值,相应的特征向量为a1,不妨设a1已单位化。把a1扩充为Rn的标准正交基a1, a2,…, an,构造矩阵X=(a2,…, an)和P=(a1,X),则P为正交矩阵且有:
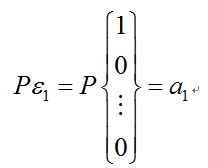
于是,AP = (Aa1, AX)= (λ1a1, P(P-1AX)) = (λ1Pε1,P(P-1AX)) = P(λ1ε1, P-1AX)。设:

【个人理解:A->n*n,X->n*n-1,P->n*n,则P-1AX->n*n-1,正好这么拆,a’->1*n-1】
从而有:
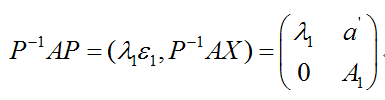
根据归纳假设,对于A1有n-1阶正交矩阵T,使得T-1A1T = TTA1T= At为上三角矩阵,现取:
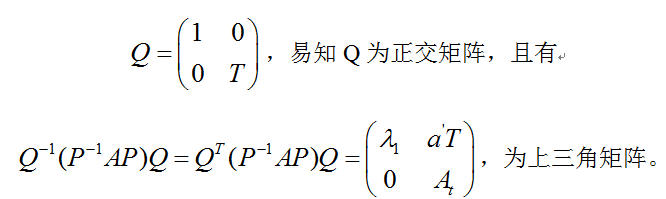
由于P和Q都是正交矩阵,而正交矩阵相乘结果R仍是正交矩阵,因此可以写作:
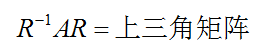
现在回到定理1的证明,因为A为实对称矩阵,则有引理1知,A的特征值均为实数。由引理2知,存在正交矩阵R,使得
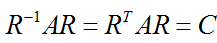
C为上三角矩阵,而A=AT,则有C=CT,但C是上三角矩阵,CT为下三角矩阵,所以C必为对角矩阵。定理1得证。其中,C的对角线元素即为A的特征值构成。
定理2(奇异值分解):
设A∈Rrm*n,则存在m阶正交矩阵U和n阶正交矩阵V,使得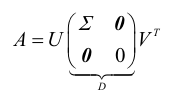
其中,Σ = diag(σ1,σ2,…, σr),即σ1, σ2,…,σr是A的非零奇异值,亦记作A=UDVT
证明:
记对称矩阵ATA的特征值为:
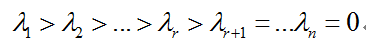
由对称矩阵的正交分解(定理1),我们有:
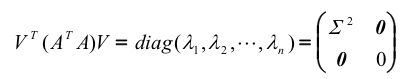
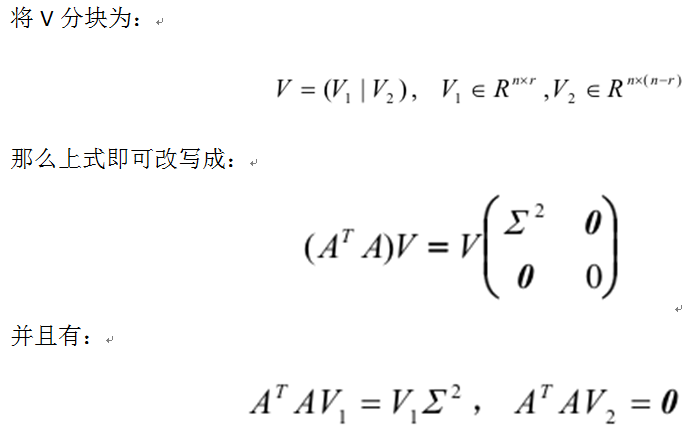
由第一个公式可以得到,
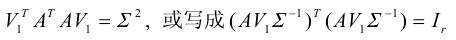
由第二个公式可以得到,
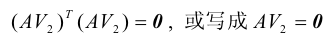

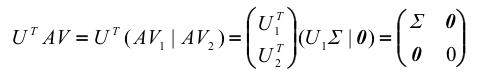
故有
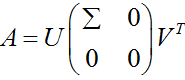
,证毕
若记U=(u1, u2,…,um),V=(v1, v2,…,vn),根据SVD的分解,A可以表示为:
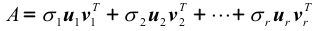
上式就是A的奇异值分解过程。
二、SVD奇异值分解求解及实现
上面的一堆推导,只是为了说明对任意矩阵都存在奇异值分解,而没有讲述如何求解奇异值分解。以下内容来自《徐士良C常用算法程序集(第二版)》,一般实矩阵的奇异值分解:
用household变换和变形QR算法对一般实矩阵进行奇异值分解,得到左右奇异向量U、V及奇异值矩阵D。
[个人认为具体怎么求SVD,大家不要去记和理解了,要用的时候能找到源码,方便其他移植即可]
例:求下面两个矩阵A和B的奇异值分解,ε取0.000001

三、SVD应用实例
1. 基于SVD的图像压缩
这个例子比较简单,首先进行奇异值分解,得到奇异值矩阵,和左右奇异向量。然后由于只要很少的奇异值,就能包含绝大部分被分解的矩阵信息,因此我们挑选不同数量的奇异值,重构图像,比较差异。这边分别实现了灰度图、RGB三色图的SVD分解。【奇异值到底选多少,自己打印奇异值矩阵,从大到小排序的,小到什么程度就舍弃,实际情况实际操作。。。】
结果:


效果图:


注意:SVD压缩只是为了存储更少的数据来表达原始图像,在重构图像时,奇异值矩阵仍旧是要和原始图像大小一样的,只不过大部分地方用0填充罢了。
相关文章推荐
- 【JavaScript】——基础(一)
- android屏幕适配详解
- 矩阵求导小结
- Android解析四种启动模式
- android wheelView
- opencv 灰度直方图 一维直方图
- 点选择的总结一
- Bengio最新博文:深度学习展望
- Xcode快捷键
- ipc\$详细用法介绍
- poj
- 知识分子真正的悲哀是依附强权放弃说理
- win7/8.1点击鼠标右键时候很慢迟迟才有反应的解决方法
- 并查集(保存分组结果)
- iOS开发 ----- vim相关以及常用shell命令
- delphi 遍历控件
- linux下使用crontab实现定时PHP计划任务失败的原因分析
- 【数据库范式】第二范式分析
- NGUI--SpringPanel总结
- maven实战学习(二)--------------maven安装和配置
