[hihoCoder] 第五十二周: 连通性·一

题目1 : 连通性·一

时间限制:10000ms
单点时限:1000ms
内存限制:256MB

描述

还记得上次小Hi和小Ho学校被黑客攻击的事情么，那一次攻击最后造成了学校网络数据的丢失。为了避免再次出现这样的情况，学校决定对校园网络进行重新设计。

学校现在一共拥有N台服务器(编号1..N)以及M条连接，保证了任意两台服务器之间都能够通过连接直接或者间接的数据通讯。

当发生黑客攻击时，学校会立刻切断网络中的一条连接或是立刻关闭一台服务器，使得整个网络被隔离成两个独立的部分。

举个例子，对于以下的网络：



每两个点之间至少有一条路径连通，当切断边(3,4)的时候，可以发现，整个网络被隔离为{1，2，3}，{4，5，6}两个部分：



若关闭服务器3，则整个网络被隔离为{1，2}，{4，5，6}两个部分：



小Hi和小Ho想要知道，在学校的网络中有哪些连接和哪些点被关闭后，能够使得整个网络被隔离为两个部分。

在上面的例子中，满足条件的有边(3,4)，点3和点4。

提示：割边&割点

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2个正整数，u,v。表示存在一条边(u,v)，连接了u,v两台服务器。1≤u<v≤N

保证输入所有点之间至少有一条连通路径。

输出

第1行：若干整数，用空格隔开，表示满足要求的服务器编号。从小到大排列。若没有满足要求的点，该行输出Null

第2..k行：每行2个整数，(u,v)表示满足要求的边，u<v。所有边根据u的大小排序，u小的排在前，当u相同时，v小的排在前面。若没有满足要求的边，则不输出

样例输入

6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6

样例输出

3 4
3 4

小Ho：这次的问题好简单！我只要依次删除每一个节点，每一条边，然后用DFS判断一下连通性就好了。

小Hi：没那么简单啦，好好看清楚N和M的范围啦。

小Ho：@_@，N和M怎么这么大，那应该怎么办？

小Hi：其实也很容易啊。这次我们要用到的叫做Tarjan算法。首先我给你普及一点点基本的知识：

割边：在连通图中，删除了连通图的某条边后，图不再连通。这样的边被称为割边，也叫做桥。

割点：在连通图中，删除了连通图的某个点以及与这个点相连的边后，图不再连通。这样的点被称为割点。

DFS搜索树：用DFS对图进行遍历时，按照遍历次序的不同，我们可以得到一棵DFS搜索树。在上面例子中，得到的搜索树为：



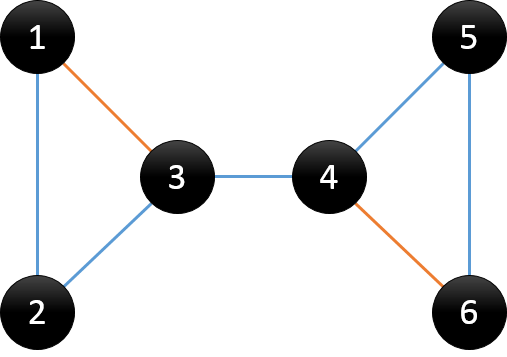
树边：在搜索树中的蓝色线所示，可理解为在DFS过程中访问未访问节点时所经过的边，也称为父子边

回边：在搜索树中的橙色线所示，可理解为在DFS过程中遇到已访问节点时所经过的边，也称为返祖边、后向边

观察DFS搜索树，我们可以发现有两类节点可以成为割点：

对根节点u，若其有两棵或两棵以上的子树，则该根结点u为割点；

对非叶子节点u（非根节点），若其子树的节点均没有指向u的祖先节点的回边，说明删除u之后，根结点与u的子树的节点不再连通；则节点u为割点。

对于根结点，显然很好处理；但是对于非叶子节点，怎么去判断有没有回边是一个值得深思的问题。

我们用dfn[u]记录节点u在DFS过程中被遍历到的次序号，low[u]记录节点u或u的子树通过非父子边追溯到最早的祖先节点（即DFS次序号最小），那么low[u]的计算过程如下：



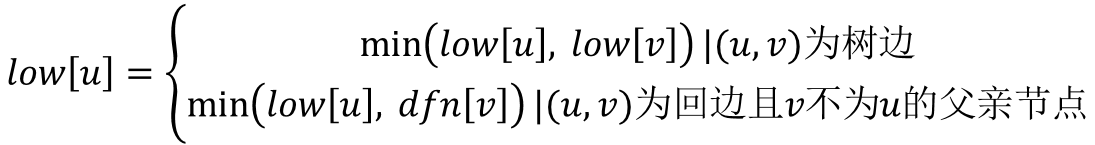
对于给的例子，其求出的dfn和low数组为：

id  1 2 3 4 5 6
dfn 1 2 3 4 5 6
low 1 1 1 4 4 4

可以发现，对于情况2，当(u,v)为树边且low[v]≥dfn[u]时，节点u才为割点。

而当(u,v)为树边且low[v]>dfn[u]时，表示v节点只能通过该边(u,v)与u连通，那么(u,v)即为割边。

Tarjan算法的代码如下：

void dfs(int u) {
//记录dfs遍历次序
static int counter = 0;

//记录节点u的子树数
int children = 0;

ArcNode *p = graph[u].firstArc;
visit[u] = 1;

//初始化dfn与low
dfn[u] = low[u] = ++counter;

for(; p != NULL; p = p->next) {
int v = p->adjvex;

//节点v未被访问，则(u,v)为树边
if(!visit[v]) {
children++;
parent[v] = u;
dfs(v);

low[u] = min(low[u], low[v]);

//case (1)
if(parent[u] == NIL && children > 1) {
printf("articulation point: %d\n", u);
}

//case (2)
if(parent[u] != NIL && low[v] >= dfn[u]) {
printf("articulation point: %d\n", u);
}

//bridge
if(low[v] > dfn[u]) {
printf("bridge: %d %d\n", u, v);
}
}

//节点v已访问，则(u,v)为回边
else if(v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}

小Ho：我大概明白了，如果这样来做，时间复杂度应该也很低吧。

小Hi：没错，它的时间复杂度是O(n+m)的，非常快。

小Ho：好！看我来实现它！

注意可能有重边，另外要注意割点要去重！

#include <bits/stdc++.h>
using namespace std;

int N, M;
int u, v;
vector<vector<int>> graph;
vector<int> dfn, low, parent;
vector<bool> visit;
set<int> art;
set<pair<int, int>> brg;
set<pair<int, int>> st1, st2;

void dfs(int u) {
static int counter = 0;
int children = 0;
visit[u] = true;
dfn[u] = low[u] = ++counter;
for (auto v : graph[u]) {
if (!visit[v]) {
++children;
parent[v] = u;
dfs(v);
low[u] = min(low[u], low[v]);
if (parent[u] == 0 && children > 1) {
art.insert(u);
}
if (parent[u] != 0 && low[v] >= dfn[u]) {
art.insert(u);
}
if (low[v] > dfn[u]) {
brg.insert({min(u, v), max(u, v)});
}
} else if (v != parent[u]) {
low[u] = min(low[u], dfn[v]);
}
}
}

void solve() {
dfs(1);
if (art.empty()) {
cout << "Null" << endl;
} else {
for (auto a : art) cout << a << " ";
cout << endl;
}
if (!brg.empty()) {
for (auto b : brg) if (st2.find(b) == st2.end()) {
cout << b.first << " " << b.second << endl;
}
}
}

int main() {
while (cin >> N >> M) {
graph.assign(N + 1, vector<int>(0));
dfn.assign(N + 1, 0);
low.assign(N + 1, 0);
parent.assign(N + 1, 0);
visit.assign(N + 1, false);
st1.clear(), st2.clear();
art.clear(), brg.clear();
for (int i = 0; i < M; ++i) {
cin >> u >> v;
graph[u].push_back(v);
graph[v].push_back(u);
if (st1.find({min(u, v), max(u, v)}) != st1.end()) {
st2.insert({min(u, v), max(u, v)});
}
st1.insert({min(u, v), max(u, v)});
}
solve();
}
return 0;
}