三维坐标系的旋转矩阵
2015-06-12 20:57
579 查看
前言:非常感谢http://m.blog.csdn.net/blog/qiuqchen/21980731的总结和分享 ,让我再一次详细的学习了三维坐标中的选择矩阵推导过程。
为了方便自己记忆,记录一下三维坐标旋转矩阵的推导过程。
坐标的旋转变换在很多地方都会用到,比如机器视觉中的摄像机标定、图像处理中的图像旋转、游戏编程等。
任何维的旋转可以表述为向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述。坐标系旋转角度θ则等同于将目标点围绕坐标原点反方向旋转同样的角度θ。
若以坐标系的三个坐标轴X、Y、Z分别作为旋转轴,则点实际上只在垂直坐标轴的平面上作二维旋转。
假设三维坐标系中的某一向量

,其在直角坐标系中的图如图1所示。其中点P在XY平面、XZ平面、YZ平面的投影分别为点M、点P、点N。

图1 直角坐标系XYZ
一、

绕Z轴旋转θ角
绕Z轴旋转,相当于

在XY平面的投影OM绕原点旋转,如下图所示,OM旋转θ角到OM'。

图4
向量绕Y轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
%5E%7BT%7D)
,则点M的坐标为

,点M'的坐标为
%5E%7BT%7D)
。由此可得:


)
)

对于
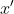
和
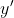
进行三角展开可得:
=xcos%5Ctheta&space;+ysin%5Ctheta)
=ycos%5Ctheta&space;-xsin%5Ctheta)
且有

;可得绕Z轴旋转

角的旋转矩阵为:
=%5Cbegin%7Bbmatrix%7D&space;cos%5Ctheta&space;&&space;sin%5Ctheta&space;&&space;0%5C%5C&space;-sin%5Ctheta&space;&&space;cos%5Ctheta&space;&&space;0%5C%5C&space;0&space;&&space;0&space;&&space;1&space;%5Cend%7Bbmatrix%7D)
二、

绕X轴旋旋转θ角
绕X轴旋转,相当于

在YZ平面的投影ON绕原点旋转,如下图所示,ON旋转θ角到ON'。

图3
向量绕X轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
%5E%7BT%7D)
,则点N的坐标为

,点N'的坐标为
%5E%7BT%7D)
。由此可得:
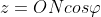
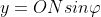
)
)

对于

和
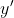
进行三角展开可得:
=zcos%5Ctheta&space;-ysin%5Ctheta)
=ycos%5Ctheta&space;+zsin%5Ctheta)
且有

;可得绕X轴旋转

角的旋转矩阵为:
=%5Cbegin%7Bbmatrix%7D&space;1&space;&&space;0&space;&&space;0%5C%5C&space;0&space;&&space;cos%5Ctheta&space;&&space;sin%5Ctheta%5C%5C&space;0&space;&&space;-sin%5Ctheta&space;&&space;cos%5Ctheta&space;%5Cend%7Bbmatrix%7D)
三、

绕Y轴旋旋转θ角
绕Y轴旋转,相当于

在XZ平面的投影OQ绕原点旋转,如下图所示,OQ旋转θ角到OQ'。

图4
向量绕Y轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
%5E%7BT%7D)
,则点Q的坐标为

,点Q'的坐标为
%5E%7BT%7D)
。由此可得:
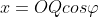
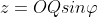
)
)

对于
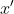
和

进行三角展开可得:
=xcos%5Ctheta&space;-zsin%5Ctheta)
=zcos%5Ctheta&space;+xsin%5Ctheta)
且有

;可得绕Y轴旋转

角的旋转矩阵为:
=%5Cbegin%7Bbmatrix%7D&space;cos%5Ctheta&space;&&space;0&space;&&space;-sin%5Ctheta%5C%5C&space;0&space;&&space;1&space;&&space;0%5C%5C&space;sin%5Ctheta&space;&&space;0&space;&&space;cos%5Ctheta&space;%5Cend%7Bbmatrix%7D)
四、绕X、Y、Z轴旋转的旋转矩阵分别为:
=%5Cbegin%7Bbmatrix%7D&space;1&space;&&space;0&space;&&space;0%5C%5C&space;0&space;&&space;cos%5Ctheta&space;&&space;sin%5Ctheta%5C%5C&space;0&space;&&space;-sin%5Ctheta&space;&&space;cos%5Ctheta&space;%5Cend%7Bbmatrix%7D)
=%5Cbegin%7Bbmatrix%7D&space;cos%5Ctheta&space;&&space;0&space;&&space;-sin%5Ctheta%5C%5C&space;0&space;&&space;1&space;&&space;0%5C%5C&space;sin%5Ctheta&space;&&space;0&space;&&space;cos%5Ctheta&space;%5Cend%7Bbmatrix%7D)
=%5Cbegin%7Bbmatrix%7D&space;cos%5Ctheta&space;&&space;sin%5Ctheta&space;&&space;0%5C%5C&space;-sin%5Ctheta&space;&&space;cos%5Ctheta&space;&&space;0%5C%5C&space;0&space;&&space;0&space;&&space;1&space;%5Cend%7Bbmatrix%7D)
五、总结
啰啰嗦嗦终于打完所有的公式了,其实三个轴会推导其中一个轴的旋转矩阵的话,另外两个轴也类似地可以很容易推导出来。这里给出所有的推导过程只是为了我自己记忆的方便。当然也可以不旋转向量,而使用旋转坐标系的方法推导,两种方法是等价的。
公式的输入我使用了这篇博客http://blog.csdn.net/linraise/article/details/11712937给出的方法。还有一个小技巧,就是可以双击公式,在最上面的工具栏“图片”选项里直接修改公式的内容。
参考:
1、《学习OpenCV》
2、公式输入:http://blog.csdn.net/linraise/article/details/11712937
3、在线编辑公式:http://www.codecogs.com/latex/eqneditor.php
扩展:
在进行图像程序开发的过程中,免不了要对图像做各种变换处理。有的时候变换可能比较复杂,比如平移之后又旋转,旋转之后又平移,又缩放。
直接用公式计算,不但复杂,而且效率低下。这时可以借助变换矩阵和矩阵乘法,将多个变换合成一个。 最后只要用一个矩阵对每个点做一次处理就可以得到想要的结果。
另外,矩阵乘法一般有硬件支持,比如3D 图形加速卡,处理3D变换中的大量矩阵运算,比普通CPU 要快上1000倍。
下面是3类基本的3D图形变换: (2D图形的变换相当于在3D的变换上减少一个维度即可)
一、平移:
设某点向x方向移动 dx, y方向移动 dy ,z方向移动dz, [x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
则 X = x+dx; Y = y+dy; Z =z+dz
以矩阵表示:

其中

即为平移矩阵。
二、旋转:
设某点与原点连线和X轴夹角为

度,以原点为圆心,绕z轴逆时针旋转

度 , 原点与该点连线长度为R, [x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
ZE

其中

即为旋转矩阵。
同理,假如绕x轴旋转

度,则旋转矩阵为:

绕y轴旋转

度,则旋转矩阵为:

三、缩放:
设某点坐标,在x轴方向扩大 sx倍,y轴方向扩大 sy倍,z轴方向扩大sz倍,[x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
X = sx*x; Y = sy*y; Z=sz*z

其中

j即为旋转矩阵。
所以复杂的3D模型视图变换都可以分解为上述三种变换,注意矩阵相乘顺序等于变换顺序。
为了方便自己记忆,记录一下三维坐标旋转矩阵的推导过程。
坐标的旋转变换在很多地方都会用到,比如机器视觉中的摄像机标定、图像处理中的图像旋转、游戏编程等。
任何维的旋转可以表述为向量与合适尺寸的方阵的乘积。最终一个旋转等价于在另一个不同坐标系下对点位置的重新表述。坐标系旋转角度θ则等同于将目标点围绕坐标原点反方向旋转同样的角度θ。
若以坐标系的三个坐标轴X、Y、Z分别作为旋转轴,则点实际上只在垂直坐标轴的平面上作二维旋转。
假设三维坐标系中的某一向量

,其在直角坐标系中的图如图1所示。其中点P在XY平面、XZ平面、YZ平面的投影分别为点M、点P、点N。

图1 直角坐标系XYZ
一、

绕Z轴旋转θ角
绕Z轴旋转,相当于

在XY平面的投影OM绕原点旋转,如下图所示,OM旋转θ角到OM'。

图4
向量绕Y轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
,则点M的坐标为

,点M'的坐标为
。由此可得:
对于
和
进行三角展开可得:
且有
;可得绕Z轴旋转

角的旋转矩阵为:
二、

绕X轴旋旋转θ角
绕X轴旋转,相当于

在YZ平面的投影ON绕原点旋转,如下图所示,ON旋转θ角到ON'。

图3
向量绕X轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
,则点N的坐标为

,点N'的坐标为
。由此可得:
对于
和
进行三角展开可得:
且有
;可得绕X轴旋转

角的旋转矩阵为:
三、

绕Y轴旋旋转θ角
绕Y轴旋转,相当于

在XZ平面的投影OQ绕原点旋转,如下图所示,OQ旋转θ角到OQ'。

图4
向量绕Y轴旋转示意图
设旋转前的坐标为

,旋转后的坐标为
,则点Q的坐标为

,点Q'的坐标为
。由此可得:
对于
和
进行三角展开可得:
且有
;可得绕Y轴旋转

角的旋转矩阵为:
四、绕X、Y、Z轴旋转的旋转矩阵分别为:
五、总结
啰啰嗦嗦终于打完所有的公式了,其实三个轴会推导其中一个轴的旋转矩阵的话,另外两个轴也类似地可以很容易推导出来。这里给出所有的推导过程只是为了我自己记忆的方便。当然也可以不旋转向量,而使用旋转坐标系的方法推导,两种方法是等价的。
公式的输入我使用了这篇博客http://blog.csdn.net/linraise/article/details/11712937给出的方法。还有一个小技巧,就是可以双击公式,在最上面的工具栏“图片”选项里直接修改公式的内容。
参考:
1、《学习OpenCV》
2、公式输入:http://blog.csdn.net/linraise/article/details/11712937
3、在线编辑公式:http://www.codecogs.com/latex/eqneditor.php
扩展:
在进行图像程序开发的过程中,免不了要对图像做各种变换处理。有的时候变换可能比较复杂,比如平移之后又旋转,旋转之后又平移,又缩放。
直接用公式计算,不但复杂,而且效率低下。这时可以借助变换矩阵和矩阵乘法,将多个变换合成一个。 最后只要用一个矩阵对每个点做一次处理就可以得到想要的结果。
另外,矩阵乘法一般有硬件支持,比如3D 图形加速卡,处理3D变换中的大量矩阵运算,比普通CPU 要快上1000倍。
下面是3类基本的3D图形变换: (2D图形的变换相当于在3D的变换上减少一个维度即可)
一、平移:
设某点向x方向移动 dx, y方向移动 dy ,z方向移动dz, [x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
则 X = x+dx; Y = y+dy; Z =z+dz
以矩阵表示:

其中

即为平移矩阵。
二、旋转:
设某点与原点连线和X轴夹角为

度,以原点为圆心,绕z轴逆时针旋转

度 , 原点与该点连线长度为R, [x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
ZE

其中

即为旋转矩阵。
同理,假如绕x轴旋转

度,则旋转矩阵为:

绕y轴旋转

度,则旋转矩阵为:

三、缩放:
设某点坐标,在x轴方向扩大 sx倍,y轴方向扩大 sy倍,z轴方向扩大sz倍,[x,y,z]为变换前坐标, [X,Y,Z]为变换后坐标。
X = sx*x; Y = sy*y; Z=sz*z

其中

j即为旋转矩阵。
所以复杂的3D模型视图变换都可以分解为上述三种变换,注意矩阵相乘顺序等于变换顺序。
相关文章推荐
- 4.2 模型变换和视图变换
- OpenGl 学习——三种变换的理解
- Unity3D -- 常用函数和变量(Shader学习之一)
- (4)应用投影和相机视口
- 三维图形矩阵变换
- OpenGL之矩阵变换Matrix
- opengl的GL_PROJECTION变换矩阵
- unigine 三维旋转矩阵(mat3,quat) 变换矩阵(mat4) 和forward up right 关系
- Bootstrap居中方法
- Markdown大赛二等奖
- Task 6.4 冲刺Two之站立会议8
- Visual studio 2010 远程调试C#程序
- 网络请求
- C++中的explicit
- 快速排序及优化(Java版)
- 词向量概况
- 后缀数组模板 SuffixArray
- SpringMVC学习(二)
- Task 6.4 冲刺Two之站立会议7
- HDU 2861 (DP+打表)
