Prove König's theorem
2015-05-21 20:19
253 查看
Problem Statement: König’s theorem describes an equivalence between the maximum matching and the minimum vertex cover problem in bipartite graphs. This is a problem in the mathematical area of graph theory.
Recently approximation algorithm course, this problem is presented as an exercise. I spent quite a lot of time on this and want to depict this problem and some related knowledge here as a kind of note.
A lecture note on this problem
Formal Definition
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.
A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched.
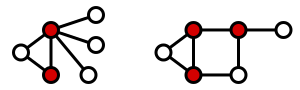
A maximum matching (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. There may be many maximum matchings. The matching number ν(G) of a graph G is the size of a maximum matching. Note that every maximum matching is maximal, but not every maximal matching is a maximum matching. The following figure shows examples of maximum matchings in the same three graphs.
Formal Definition
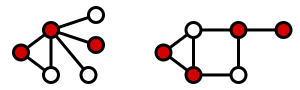
Formally, a vertex-cover of an undirected graph G=(V, E) is a subset V′ of V such that if edge (u, v) is an edge of G, then u is in V′, or v is in V′, or both. The set V′ is said to “cover” the edges of G. The following figure shows examples of vertex covers in two graphs (and the set V’ is marked with red).
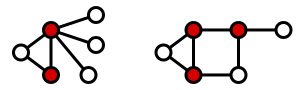
A minimum vertex cover is a vertex cover of smallest possible size. The vertex cover number \tau is the size of a minimum vertex cover. The following figure shows examples of minimum vertex covers in the previous graphs.

G=(V,E) : a bipartite graph
L and R: Divide the vertex set into the left set L and the right set R
M : A maximum matching for G
No vertex in a vertex cover can cover more than one edge of M (because the edge half-overlap would prevent M from being a matching in the first place), so if a vertex cover with |M| vertices can be constructed, it must be a minimum cover.
没有看懂wiki上的证明过程,但是在另外一个博客上看到了更intuitive的证明如下:
首先,最小点集覆盖一定>=最大匹配,因为假设最大匹配为n,那么我们就得到了n条互不相邻的边,光覆盖这些边就要用到n个点。
现在我们来思考为什么最小点击覆盖一定<=最大匹配。
任何一种n个点的最小点集覆盖,一定可以转化成一个n的最大匹配。因为最小点集覆盖中的每个点都能找到至少一条只有一个端点在点集中的边。
如果找不到则说明该点所有的边的另外一个端点都被覆盖,所以该点则没必要被覆盖,和它在最小点集覆盖中相矛盾。
多个覆盖点都只能选则同一个点组成匹配的情况是不会出现的。因为如果出现这种情况的话,那么这几个点一定不是最小点集覆盖。因为这几个点(设为点集合S)既然只有一个点A可以组成匹配,说明这些S中的点除去与点A的边之外的其他边的另一端都是覆盖点,即S中点的其他边都已被其他点覆盖到,S里点被选为覆盖集是要覆盖S与A连接的那条边,所以最小点集覆盖应该选那个点A即可覆盖这些边,而不选S中的点。
只要每个端点都选择一个这样的边,就必然能转化为一个匹配数与点集覆盖的点数相等的匹配方案。所以最大匹配至少为最小点集覆盖数,即最小点集覆盖一定<=最大匹配。
参考资料
Recently approximation algorithm course, this problem is presented as an exercise. I spent quite a lot of time on this and want to depict this problem and some related knowledge here as a kind of note.
A lecture note on this problem
1. Background
1.1 Matching and the Maximum Matching wiki
A matching in a graph is a set of edges no two of which share an endpoint, and a matching is maximum if no other matching has more edges.Formal Definition
Given a graph G = (V,E), a matching M in G is a set of pairwise non-adjacent edges; that is, no two edges share a common vertex.
A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched.
A maximum matching (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. There may be many maximum matchings. The matching number ν(G) of a graph G is the size of a maximum matching. Note that every maximum matching is maximal, but not every maximal matching is a maximum matching. The following figure shows examples of maximum matchings in the same three graphs.

1.2 Vertex Cover and the Minimum Vertex Cover wiki
A vertex cover in a graph is a set of vertices that includes at least one endpoint of each edge, and a vertex cover is minimum if no other vertex cover has fewer verticesFormal Definition
Formally, a vertex-cover of an undirected graph G=(V, E) is a subset V′ of V such that if edge (u, v) is an edge of G, then u is in V′, or v is in V′, or both. The set V′ is said to “cover” the edges of G. The following figure shows examples of vertex covers in two graphs (and the set V’ is marked with red).

A minimum vertex cover is a vertex cover of smallest possible size. The vertex cover number \tau is the size of a minimum vertex cover. The following figure shows examples of minimum vertex covers in the previous graphs.

1.3 Bipartite Graph wiki
A graph is bipartite if its vertices can be partitioned into two sets such that each edge has one endpoint in each set
2. Proof of König’s theorem
2.1 According To Wikipedia
SettingG=(V,E) : a bipartite graph
L and R: Divide the vertex set into the left set L and the right set R
M : A maximum matching for G
No vertex in a vertex cover can cover more than one edge of M (because the edge half-overlap would prevent M from being a matching in the first place), so if a vertex cover with |M| vertices can be constructed, it must be a minimum cover.
没有看懂wiki上的证明过程,但是在另外一个博客上看到了更intuitive的证明如下:
首先,最小点集覆盖一定>=最大匹配,因为假设最大匹配为n,那么我们就得到了n条互不相邻的边,光覆盖这些边就要用到n个点。
现在我们来思考为什么最小点击覆盖一定<=最大匹配。
任何一种n个点的最小点集覆盖,一定可以转化成一个n的最大匹配。因为最小点集覆盖中的每个点都能找到至少一条只有一个端点在点集中的边。
如果找不到则说明该点所有的边的另外一个端点都被覆盖,所以该点则没必要被覆盖,和它在最小点集覆盖中相矛盾。
多个覆盖点都只能选则同一个点组成匹配的情况是不会出现的。因为如果出现这种情况的话,那么这几个点一定不是最小点集覆盖。因为这几个点(设为点集合S)既然只有一个点A可以组成匹配,说明这些S中的点除去与点A的边之外的其他边的另一端都是覆盖点,即S中点的其他边都已被其他点覆盖到,S里点被选为覆盖集是要覆盖S与A连接的那条边,所以最小点集覆盖应该选那个点A即可覆盖这些边,而不选S中的点。
只要每个端点都选择一个这样的边,就必然能转化为一个匹配数与点集覆盖的点数相等的匹配方案。所以最大匹配至少为最小点集覆盖数,即最小点集覆盖一定<=最大匹配。
参考资料
相关文章推荐
- how to prove concurrent algorithms are correct
- [AI]贝叶斯定理 Bayes' theorem
- A field guide to algebra,theorem 1.1.3
- 读控制台HDU 1788 Chinese remainder theorem again 数论读控制台
- POJ 3006 Dirichlet's Theorem on Arithmetic Progressions
- HDU 1788 Chinese remainder theorem again 中国剩余定理转换
- How to beat the CAP theorem--笔记
- hdu 3689 杭州 10 现场 J - Infinite monkey theorem 概率dp kmp 难度:1
- 暴力 Codeforces Round #183 (Div. 2) A. Pythagorean Theorem II
- Mercer's Theorem的证明
- 策梅洛定理 (博弈论): Zermelo's theorem
- POJ3006_Dirichlet's Theorem on Arithmetic Progressions_筛法求素数表
- Prove the EXACT 4SAT is NP-complete.
- Euler theorem(水)
- POJ3006 Dirichlet's Theorem on Arithmetic Progressions【筛选法】
- 杭州现场J题_Infinite monkey theorem
- Pythagoras' Theorem
- HDU1788 Chinese remainder theorem again
- hdu 3689 Infinite monkey theorem dp
- uva 11178 Morley's Theorem 点线
