Abstract Data Type(ADT)

Abstract Data Type(ADT)

Abstract Data TypeADT
ArrayList

StringBuffer

Linked List
Singly Linked List

Doubly Linked List

Map

Hash Table

Tree
Binary Tree

Complete Binary Tree

Binary Search Tree

Heap

Priority Queue

ArrayList

Properties:

Advantage:

Dynamically Resizing Array.

It is an array that resizes itself as needed while still providing O(1) access. A typical implementation is that when array is full, the array doubles in size . Each doubling takes O(b) time, but happens so rarely that is amortized time is still O(1).

StringBuffer

Properties:

Advantages:

StringBuffer simply creates an array of all the strings, copying them back to a string when necessary. Details please refer “Cracking the interview” - Data Structure - Chapter 1 and “String和StringBuffer详解” in this blog.

Simple Implementation:

public class MyStringBuffer {
protected char [] value;
protected int capacity;
protected int count;

public MyStringBuffer(){
capacity = 16;
value = new char[capacity];
count = 0;
}

public MyStringBuffer append(String str){
int len = str.length();
int newCount = count + len;
if(newCount > capacity){
expandCapacity(newCount);
}
char[] src = str.toCharArray();
System.arraycopy(src, 0, value, count, len);
/*
*public static void arraycopy(Object src,
int srcPos,
Object dest,
int destPos,
int length)
*/
count = newCount;
return this;
}

public String toString(){
return String.valueOf(value, 0, count);
}

protected void expandCapacity(int newCapacity){
if(newCapacity > 2*capacity){
capacity = newCapacity;
}
else{
capacity = 2*capacity;
}
value = new char[capacity];
}

public static void main(String[] args)
{
MyStringBuffer sb = new MyStringBuffer();
sb.append("123").append("456");
System.out.println(sb);

}
}

Linked List

Singly Linked List

Properties:

Advantage:

Adaptable compared to Arrays which have fixed size N.

Easy to insert elements

Disadvantage: Hard to remove elements when given the Node, because we cannot get the previous Node directly.

Simple Implementation:

class Node<T>{
T element;
Node<T> next;

public Node(T e, Node<T> n){
element = e;
next = n;
}
}

class SinglyLinkedList<T>
{
Node<T> head;
int size;

public SinglyLinkedList(){
head = null<
4000
/span>;
size = 0;
}

void addFirst(T data){
Node<T> newHead = new Node<T>(data, head);
head = newHead;
size++;
}

void addLast(T data){
Node<T> temp = head;
while(temp.next != null){
temp = temp.next;
}
temp.next = new Node<T>(data, null);
size++;
}
}

Doubly Linked List

Properties:

Advantage: Easy to remove elements compared to the Singly Linked List

Implementation:

class DNode<T>{
protected T element;
protected DNode<T> next, prev;

public DNode(T e, DNode<T> n, DNode<T> p){
element = e;
next = n;
prev = p;
}

public DNode<T> getNext(){return next;}
public DNode<T> getPrev(){return prev;}
public T getElement(){return element;}
public void setNext(DNode<T> n){next = n;}
public void setPrev(DNode<T> p){prev = p;}
public void setElement(T e){element = e;}
}

public class DList<T> {
protected DNode<T> head, tail;
protected int size;

public DList(){
size = 0;
head = new DNode<T>(null, null, null);
tail = new DNode<T>(null, null, head);
head.setNext(tail);
}

public int size(){return size;}

public boolean isEmpty(){return (size == 0);}

public DNode<T> getFisrt() throws IllegalStateException {
if(isEmpty()) throw new IllegalStateException("List is empty");
return head.getNext();
}

public DNode<T> getLast() throws IllegalStateException{
if(isEmpty()) throw new IllegalStateException("List is empty");
return tail.getPrev();
}

public DNode<T> getNext(DNode<T> n) throws IllegalStateException{
if(n == tail) throw new IllegalStateException("Cannot move forward past the tail of the list");
return n.getNext();
}

public DNode<T> getPrev(DNode<T> n) throws IllegalStateException{
if(n == head) throw new IllegalStateException("Cannot move back past the head of the list");
return n.getPrev();
}

public void addBefore(DNode<T> n, DNode<T> m) throws IllegalStateException{
DNode<T> p = getPrev(n); //may throw an IllegalStateException
p.setNext(m);
m.setPrev(p);

m.setNext(n);
n.setPrev(m);

size++;
}

public void addAfter(DNode<T> n, DNode<T> m) throws IllegalStateException{
DNode<T> a = getNext(n); //may throw an IllegalStateException
n.setNext(m);
m.setPrev(n);

a.setPrev(m);
m.setNext(a);

size++;
}

public void addFirst(DNode<T> n){
addAfter(head, n);
}

public void addLast(DNode<T> n){
addBefore(tail, n);
}

public void remove(DNode<T> n){
DNode<T> p = getPrev(n); //may throw an IllegalStateException
DNode<T> a = getNext(n); //may throw an IllegalStateException

p.setNext(a);
a.setPrev(p);

n = null;
size--;
}

public boolean hasPrev(DNode<T> n){return n != head;}

public boolean hasNext(DNode<T> n){return n != tail;}

public String toString(){
String s = "[";
DNode<T> n = head.getNext();
while(n != tail){
s += n.getElement();
n = n.getNext();
if(n != tail){
s += ",";
}
}
s += "]";
return s;
}
}

Map

Properties:

A map models a searchable collection of key-value entries

The main operations of a map are for searching, inserting, and deleting items

Multiple entries with the same key are not allowed

Methods:

get(k): if the map M has an entry with key k, return its

associated value; else, return null

put(k, v): insert entry (k, v) into the map M; if key k is not

already in M, then return null; else, return old value

associated with k

remove(k): if the map M has an entry with key k, remove

it from M and return its associated value; else, return null

size(), isEmpty()

entrySet(): return an iterable collection of the entries in M

keySet(): return an iterable collection of the keys in M

values(): return an iterator of the values in M

Performance:

put takes O(1) time since we can insert the new item at the beginning or at the end of the sequence

get and remove take O(n) time since in the worst case (the item is not found) we traverse the entire sequence to look for an item with the given key

Simple List-Based Map Implementation (extends from DList above):

class Entry<K, V>{
protected K key;
protected V value;

public Entry(K k, V v){
key = k;
value = v;
}

K getKey(){return key;}
V getValue(){return value;}
void setKey(K k){key = k;}
void setValue(V v){value = v;}
}

public class ListMap<K,V> extends DList<Entry<K,V>>{
public V get(K k){
DNode<Entry<K, V>> n = head.getNext();
while(n != tail){
if(n.getElement().getKey() == k){
return n.getElement().getValue();
}
n = n.getNext();
}
return null;
}

public V put(K k, V v){
DNode<Entry<K, V>> n = head.getNext();
while(n != tail){
if(n.getElement().getKey() == k){
V t = n.getElement().getValue();
n.setElement(new Entry<K, V>(k, v));
return t;
}
n = n.getNext();
}
Entry<K,V> e = new Entry<K,V>(k,v);
addLast(new DNode<Entry<K,V>>(e,null,null));
return null;
}

public V remove(K k){
DNode<Entry<K, V>> n = head.getNext();
while(n != tail){
if(n.getElement().getKey() == k){
V t = n.getElement().getValue();
remove(n);
return t;
}
n = n.getNext();
}
return null;
}
}

Hash Table

Properties:

Advantage: Realization of direct addressing

Direct Addressing: With an array T, we store the element whose key is k at slot T[k]. We find the element whose key is k by looking up T[k], which means O(1)

Time Consuming: The expected time to search for an element in a hash table is O(1), under some reasonable assumptions. Worst-case search time is O(n) however.

Principle:

24000

Hash Table:

A hash table for a given key type consists of

Hash function h

Bucket Array (called table) of size N

When implementing a map with a hash table, the goal is to store entry (key,value) at index i=h(key) in Bucket Array

Hash Functions:

A hash function h maps keys of a given type to integers in a fixed interval [0,N−1].

For example: h(x)=x(modN)is a hash function for integer keys.

The integer h(x) is called the hash value of key x

A good hash function can

Minimize the collision

Fast and easy to computer

A hash function is usually specified as the composition of two functions:

Hash code: h1:keys→integers

Compression function: h2:integers→[0,N−1]

Hash Code:

A good Hash code is aim to avoid the collision.

Some common Hash Code realization:

Memory Address:

We reinterpret the memory address of the key object as an integer (default hash code of all Java objects)

Good in general, except for numeric and string keys (Same Strings my have the different memory addresses)

Integer cast:

We reinterpret the bits of the key as an integer

Suitable for keys of length less than or equal to the number of bits of the integer type (e.g., byte, short, int and float in Java)

Component sum:

We partition the bits of the key into components of fixed length (32 bits) and we sum the components (ignoring overflows)

For example (if the type of key is long):

static int hashCode(long i) {return (int)((i >> 32) + (int)i)};

Suitable for numeric keys of fixed length greater than or equal to the number of bits of the integer type (e.g., long and double in Java)

Polynomial accumulation:

Component sum is not a good choice for string. For example, “stop”. “tops”, “pots”, “spot” will have the same hash code. So, we need Polynomial accumulation

We partition the bits of the key into a sequence of components of fixed length (e.g., 8, 16 or 32 bits)a0,a1,a2,...an−1

We evaluate the polynomialp(z)=a0+a1z+a2z2+...+an−1zn−1at a fixed value z, ignoring overflows

Especially suitable for strings (e.g., the choice z = 33 gives at most 6 collisions on a set of 50,000 English words)

Polynomial p(z) can be evaluated in O(n) time using Horner’s rule:p(z)=a0+(a1+...+(an−3+(an−2+an−1z)z)...)z p0(z)=an−1 pi(z)=an−i−1+pi−1(z)zwhere i=1,2,...,n−1we have p(z)=pn−1(z)

Cyclic Shift Hash Code:

A variant of the polynomial hash code replaces multiplication by a with a cyclic shift of a partial sum by a certain number of bits.

Comparison of collision behavior for the cyclic shift variant of the polynomial hash code as applied to a list of just over 25,000 English words. The “Total” column records the total number of collisions and the “Max” column records the maximum number of collision for any one hash code.



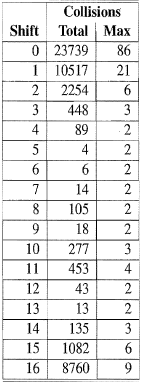
Simple implementation:

static int hashCode(String){
int h = 0;
for(int i = 0;i < s.length();i++){
h = (h << 5) | (h >>> 27);//5-bit cyclic shift of the running sum
h += (int)s.charAt(i);//add in next character
}
}

Compression Functions:

Division Method:

h2(y)=y(modN)

The size N of the hash table is usually chosen to be a prime

MAD (Multiple-Add and Divide):

h2(y)=[(ay+b)(modp)](modN)

N is the size of the bucket array, p is a prime number larger than N, and a and b are integers chosen at random from the interval [0,p−1], with a>0.

Collision Handling:

Collisions occur when different elements are mapped to the same cell

Some common methods:

Separate Chaining:

let each cell in the table point to a linked list of entries that map there

Separate chaining is simple, but requires additional memory outside the table



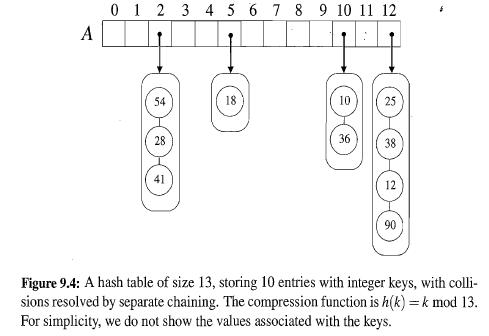
Open Addressing:

the colliding item is placed in a different cell of the table

Some common methods:

Linear Probing: Insert entry (k,v) into a bucket A[i] that is occupied, where i=h(k), then we try next at A[(i+1)(modN)]. If A[(i+1)(modN)] is occupied, we try A[(i+2)(modN)] and so on.



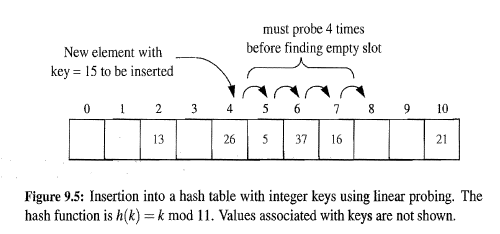
Disadvantages:

Because “search operation” will stop when it find an empty bucket. We need leave an “available” mark when we remove an entry to make the “search operation” know this bucket has been occupied.

It tends to cluster the entries of the map into contiguous runs, which may even overlap(particularly if more than half of the cells in the hash table are occupied). Such contiguous runs of occupied hash cells causes searches to slow down considerably.

Quadratic Probing: The strategy involves iteratively trying the buckets A[(i+f(j))(modN)], for j=0,1,2,..., where f(j)=j2.

Disadvantage: secondary clustering.

Double Hashing: Double hashing uses a secondary hash function d(k) and handles collisions by placing an item in the first available cell of the series (i+jd(k))(modN)for j=0,1,...,N−1

The secondary hash function d(k) cannot have zero values

The table size N must be a prime to allow probing of all the cells

Common choice of compression function for

the secondary hash function: d2(k)=q−k(modq)where q<N and q is a prime.

The possible values for d2(k) are 1,2,...,q

Performance

In the worst case, searches, insertions and removals on a hash table take O(n) time

The worst case occurs when all the keys inserted into the map collide

The load factor a=n/N affects the performance of a hash table, where n is the number of entries and N is the size of the Bucket Array

Assuming that the hash values are like random numbers, it can be shown that the expected number of probes for an insertion with open addressing is 1/(1−a)

The expected running time of all the dictionary ADT operations in a hash table is O(1)

In practice, hashing is very fast provided the load factor is not close to 100%

Simple Implementation:

import java.util.*;

public class HashTable<K,V>{
protected LinkedList<Entry<K,V>>[] bucket;
protected int capacity; //Hash value is prime
protected int n; //Number of entries

public HashTable(int cap){
capacity = cap;
bucket = (LinkedList<Entry<K,V>>[])new LinkedList[capacity];
}

public int hashValue(K k){
int hashCode = k.hashCode();
return hashCode%capacity;
}

public void add(K k, V v){
Entry<K,V> e = new Entry<K,V>(k, v);
int hv = this.hashValue(k);
if(bucket[hv] == null){
bucket[hv] = new LinkedList<Entry<K,V>>();
}
bucket[hv].add(e);
n++;
}

private Entry<K,V> findEntry(K k){
int hv = this.hashValue(k);
if(bucket[hv] == null) return null;
ListIterator li = bucket[hv].listIterator();
while(li.hasNext()){
Entry<K,V> e = (Entry<K,V>)li.next();
if(e.getKey() == k) return e;
}
return null;
}

public V get(K k){
Entry<K,V> e = this.findEntry(k);
if(e != null){
return e.getValue();
}
return null;
}

public V remove(K k){
V result = null;
int hv = this.hashValue(k);
if(bucket[hv] == null) return null;
ListIterator li = bucket[hv].listIterator();
while(li.hasNext()){
Entry<K,V> e = (Entry<K,V>)li.next();
if(e.getKey() == k){
result = e.getValue();
bucket[hv].remove(e);
n--;
break;
}
}
return result;
}

int size(){
return n;
}

boolean isEmpty(){
return n == 0;
}

void printHashTable(){
if(this.isEmpty()){
System.out.println("This Hash Table is empty!");
}
for(int i = 0;i < capacity;i++){
if(bucket[i] != null){
ListIterator<Entry<K,V>> li = bucket[i].listIterator();
while(li.hasNext()){
Entry<K,V> e = (Entry<K,V>)li.next();
System.out.print("["+e.getKey()+","+e.getValue()+"] ");
}
}
}
System.out.println();
}

class Entry<K,V>{
protected K key;
protected V value;

public Entry(K k, V v){
key = k;
value = v;
}

K getKey(){return key;}
V getValue(){return value;}

V setValue(V v){
V old = value;
value = v;
return old;
}
}

public static void main(String[] args)
{
HashTable<Integer, String> ht = new HashTable<Integer, String>(10);
ht.add(1, "Wang");
ht.add(2,"Li");
ht.printHashTable();
System.out.println(ht.get(3));
System.out.println(ht.remove(2));
ht.printHashTable();
}
}

Tree

Construction

root

parent

children

siblings

internal or external(leaves)

ancestor: A node u is an ancestor of a node v if u = v or u is an ancestor of the parent of v.

descendant: the inverse of ancestor

edge: pair of nodes

path: a sequence of nodes, combined by many edges

Depth and Height

depth: the depth of v is the number of ancestors of v, excluding v itself and the depth of the root of T is 0.

The height of a node v in a tree T is also defined recursively:

If v is an external node, then the height of v is 0

Otherwise, the height of v is one plus the maximum height of a child of v.

The height of a nonempty tree T is equal to the maximum depth of an external node of T.

Ordered

A tree is ordered if there is a linear ordering defined for the

children of each node; that is, we can identify the children of a node

as being the first, second, third, and so on.

Traversal

Inorder

Preorder

Postorder

Binary Tree

Full:

A binary tree is proper (or full) if each node has either zero or two children. A binary tree that is not proper is improper.

If a tree is full, then nE=nI+1 where nE is the number of external nodes and nI is the number of internal nodes.

Properties:

Let T be a nonempty binary tree, and let n, nE, nI and h denote the number of nodes, number of external nodes, number of internal nodes, and height of T, respectively. Then T has the following properties:

h+1≤n≤2h+1−1

1≤nE≤2h

h≤nI≤2h−1

log(n+1)−1≤h≤n−1

Also, ifT is proper, then T has the following properties:

2h+1≤n≤2h+1−1

h+1≤nE≤2h

h≤nI≤2h−1

log(n+1)−1≤h≤(n−1)/2

In a nonempty proper binary tree T, with nE external nodes and nI internal nodes, we have nE=nI+1.

Complete Binary Tree:

The difference between Full Binary Tree and Complete Binary Tree

A full binary tree (sometimes proper binary tree or 2-tree) is a tree in which every node other than the leaves has two children.


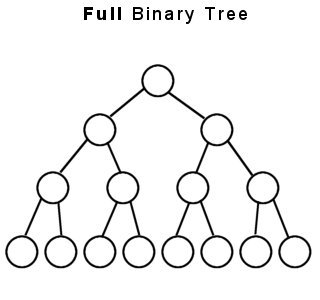
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.


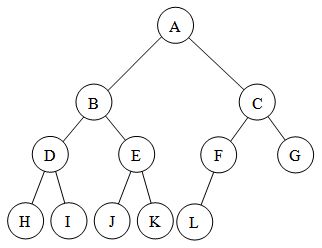
Properties:

2h≤n≤2h+1−1

h=⌊log2n⌋

The tree can be stored in an array without pointer

nI=⌊n/2⌋ becasue if the last internal node has two children, then the tree is a full tree, nE=nI+1, so n=2nI+1 and if the last internal node has one child, then nE=nI, so n=2nI.

Binary Search Tree

Time complexity of each function in the BST

height: The average time complexity of get the height of a node is T(n)=O(n) where is n is the number of children of the node

depth: The average time complexity of get the depth of a node in a Binary Tree is T(n)=O(log(n)) where n is the number of nodes of the tree

contains: average T(n)=O(log(n))

findMin and findMax: average T(n)=O(log(n))

insert: average T(n)=O(log(n))

remove: T(n)=O(log(n))

traverse: T(n)=O(n)

search:T(n)=O(log(n))

Conclusion: except height and traverse, the time-complexity of the functions in BST is T(n)=O(log(n))

Implementation:

class Node {
int value; // value of node
Node left; // left child
Node right; // right child

Node(int value) // construction
{
this.value = value;
this.left = null;
this.right = null;
}
}

//The functions that are wrote in the form of recursion can also be wrote by loop
public class BinarySearchTree {
private Node root; // root node

BinarySearchTree() {
root = null;
}

BinarySearchTree(int[] arr) {
for (int i : arr)
insert(i);
}

public int height(Node node){//O(n)
if(node == null){
return -1;
} else {
int leftHeight = height(node.left);
int rightHeight = height(node.right);
return ((leftHeight > rightHeight)? leftHeight:rightHeight)+1;
}
}

//BST does not need a parent node, but we wrote it here for the future
//  public int depth(Node node){//O(depth of the node)
//      if(node == root){
//          return 0;
//      } else {
//          return depth(node.parent)+1;
//      }
//  }

public boolean contains(int key){//O(depth of key or the depth of the null) <= O(n)
Node curr = root;
while(curr != null){
if(key < curr.value){
curr = curr.left;
} else if(key > curr.value) {
curr = curr.right;
} else {
return true;
}
}
return false;
}

//  public boolean contains(int key){
//      return contains(key, root);
//  }
//
//  private boolean contains(int key, Node node){
//      if(node == null){
//          return false;
//      } else if(key < node.value){
//          return contains(key, node.left);
//      } else if (key > node.value) {
//          return contains(key, node.right);
//      } else {
//          return true;
//      }
//  }

public Node findMin(Node node){//Recursive version, O(depth of the min node)
if(node == null)
return null;
if(node.left == null)
return node;
return findMin(node.left);
}

public Node findMax(Node node){//Non-recursive implementation O(depth of the max node)
Node curr = node;
if(curr != null){
while(curr.right != null){
curr = curr.right;
}
}
return curr;
}

public void insert(int value) {
root = insert(root, value);
}

private Node insert(Node node, int value) {// insert a value into a node O(depth of the position of the inserted value)
if (node == null)
node = new Node(value);
else if (value < node.value)
node.left = insert(node.left, value);
else
node.right = insert(node.right, value);
return node;
}

public void remove(Node node, int key){
if(node == null){
return;
}
if(key < node.value){
remove(node.left, key);
} else if(key > node.value) {
remove(node.right, key);
} else {
if(node.left != null && node.right != null){//Both children of the delNode are not null
node.value = findMin(node.right).value;
remove(node.right, node.value);
} else {//One or both of them are null
node = (node.left != null)? node.left:node.right;
}
}
}

public void visit(Node node) {
if (node == null)
return;
int value = node.value;
System.out.println(value);
}

//The time- complexity of the traverse of binary tree is O(n)
public void inOrderTraverse(Node node) {
if (node == null)
return;
else {
inOrderTraverse(node.left);
visit(node);
inOrderTraverse(node.right);
}
}

public void preOrderTraverse(Node node){
if(node == null)
return;
else {
visit(node);
preOrderTraverse(node.left);
preOrderTraverse(node.right);
}
}

public void postOrderTraverse(Node node){
if(node == null)
return;
else {
postOrderTraverse(node.left);
postOrderTraverse(node.right);
visit(node);
}
}

//O(depth of the key or the null)
public Node search(Node root, int key) {// Search
Node found;
if (root == null)
found = null;
else if (key < root.value)
found = search(root.left, key);
else if (key > root.value)
found = search(root.right, key);
else
found = root;
return found;
}

public static void main(String[] args) {
int arr[] = { 3, 5, 10, 6, 4, 12, 8, 9, 7, 2 };
BinarySearchTree bitree = new BinarySearchTree(arr);
System.out.println(bitree.search(bitree.root, 5).value);
bitree.inOrderTraverse(bitree.root);
}

}

Heap

Concept:

Complete Binary Tree

Max-heap: parents are always larger than their children

Min-heap: parents are always smaller than their children

Property

Index Relationship:

PARENT(i)

return⌊i/2⌋

LEFT(i)

return2i

RIGHT(i)

return2i+1

A[PARENT(i)]≤A[i] for Max-heap where A is the heap array

Time-Complexity of each function:

HEIGHT:Θ(lgn)

MAX−HEAPIFY:O(h) or O(lgn) where h is the height of the heap

BUILD−MAX−HEAP(A):O(n)

HEAPSORT:O(nlgn)

Realization

class Heap {
int size = 0;
int length;
int[] heap;
public Heap(int length){
this.length = length;
heap = new int[length+1];
heap[0] = Integer.MAX_VALUE;
}

private int parent(int i){
return i/2;
}

private int left(int i){
return 2*i;
}

private int right(int i){
return 2*i+1;
}

private void swap(int i, int j){
int tmp = heap[i];
heap[i] = heap[j];
heap[j] = tmp;
}

private void maxHeapify(int i){
int l = left(i), r = right(i), largest = i;
if(l <= size && heap[l] > heap[largest]){
largest = l;
}
if(r <= size && heap[r] > heap[largest]){
largest = r;
}
if(i != largest){
swap(i, largest);
maxHeapify(largest);
}
}

public void buildHeap(int[] array) {//O(n) tight bound
if(length < array.length){
heap = new int[length+1];
}
size = array.length;
for(int i = 1;i <= size;i++){
heap[i] = array[i-1];
}

//The nodes with the index from 1 to n/2 are internal nodes
//The nodes with the index form n/2+1 to n are leaves
//All the leaves can be saw as a heap with one element
//For every node, we call maxHeapify to heapify the node
//We call the maxHeapify from the last node to the root
for(int i = size/2;i >= 1;i--){
maxHeapify(i);
}
}

public int extractMax(){
int result = heap[1];
heap[1] = heap[size--];
maxHeapify(1);
return result;
}

public void insert(int num){
size++;
if(size > length){
length = size;
heap = Arrays.copyOf(heap, length+1);
}
heap[size] = num;
int i = size;
while(heap[i] > heap[parent(i)]){//We do not need to set the condition i > 1. because heap[0] = INTEGER.MAX_VALUE
swap(i, parent(i));
i = parent(i);
}
}
}

Priority Queue

Normally, a priority queue is realized by a heap(most of the time, Min-heap). In the queue, every entry is a key-value pair. The key represents the priority of the entry, just like the element value in the heap we discussed above. The core function of a priority queue is extractMin for a Min-heap (of course, extractMax for Max-heap). Therefore , we can always get the minimum or maximum value in the queue. The realization depends on the requirement and the main construction has already been realized by the heap above, so we do not realize it here. The related content please refer the Introduction to Algorithm.