9 empirical risk minimization(ERM)
2015-02-14 10:29
204 查看
本学习笔记参考自Andrew的机器学习课程(点此打开),
内容来自视频以及其讲义, 部分内容引用网友的学习笔记,会特别注明
本集内容1. 偏差/方差(Bias/variance)
2. 经验风险最小化(empirical risk minimization (ERM))
3. 联合界引理union bound/Hoeffding不等式
4. 一致收敛(uniform convergence)
开篇Andrew Ng[大概]: To me what really separeates the people that really understand and really get machine
learning compared to people that maybe read textbook and so they'll work through the math will be what you do next. When you apply a support vector machine and it doesn't quite do what you wanted, do you understand enough about svm to know what to do next
and how to modify the algorithm? And to me that's often what really separates the great people in machine learning versus the people that like read the text book and so they'll the math and so they'll have just understood that. 希望以后用这个标准来衡量自己吧!
偏差/方差折中
再次考虑线性回归的例子,对于一批样本,我们用不同的特征维度拟合出不同的模型,如下图: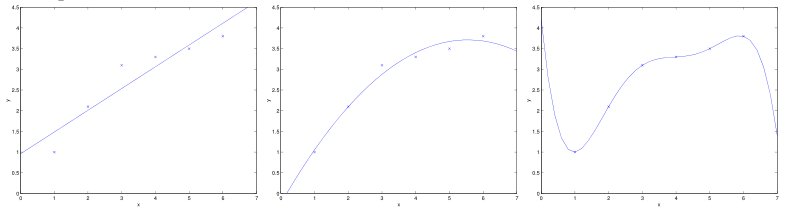
最左边的是一次函数在前面我们介绍过,属于欠拟合,最右边的拟合的是5阶函数,属于过拟合。这两个模型对于训练样本外的点预测效果都不好,一般误差都很大,一般误差是指一个假设在样本中预测出错的情况,这里的样本包括训练样本,还有训练集外的样本。对于欠拟合情况,我们可以说该算法有高偏差(低方差),因为它不能明显的拟合出数据原有的规律。对于过拟合情况,我们可以说该算法有高方差(低偏差),因为该算法拟合出了一些奇怪的规律。一个可行的方法就是在两个极端例子之间折中,即中间的图,拟合成二阶的函数。(这里并没有介绍关于偏差、方差的形式化定义,大概的直观理解一下)
经验风险最小化
为了讨论方便,我们仍然用二元分类问题来举例,这里分类输出是1或0,下面所讨论的都能推广到回归问题,多元分类问题等。现在我们假设训练集为
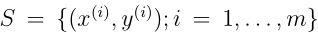
,并假设所有
都是独立同分布,它们服从一个概率分布D,对于一个假设h,我们定义训练误差(或叫经验风险,经验误差)如下:
注意如果一个符号上面有^,表面它对试图一个量进行估计,常常试图表示对一个真实量的近似,比如
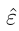
试图表示一般误差。这里的训练误差直观理解就是假设h预测错误的样本数量所占比例。此外我们定义h的一般误差:
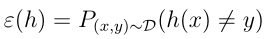
这里一般误差就不只是在训练样本中统计了,我们需要定义它是因为我们最终所关心的是模型对于训练集外的样本点是否能够正确预测,但很多情况我们只关注训练集是否拟合得够好,那么是否在训练集上的预测情况会关联着集外预测的情况呢?下面会给出答案,先介绍经验风险最小化。
令

,一种合适的选择参数θ的算法是最小化训练误差:
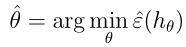
这个过程我们也叫经验风险最小化(ERM),也是我们第一个机器学习的理论。事实上ERM是一个非常基本的学习算法,我们可以从线性回归、逻辑回归中看到,最终获取参数的方式都是直接或间接的使误差最小。
下面我们再定义假设类
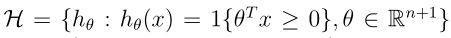
,即H是一个分类器的集合,我们将经验风险最小化用选择一个假设来表示(上面是选择参数使训练误差最小):
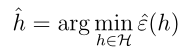
那么到此,我们引出了经验风险最小化。前面提过,我们最终是很关心一般误差的,下面要证明训练误差很小,那么一般误差也会很小,即训练误差是一般误差的很好的近似,我们会得出一致收敛的结论。然后将ERM与这个结论结合起来说明一些问题,在证明一致收敛之前,需要介绍两个引理。
联合界引理
令 A 1 ,A 2 ,...,A k 是k个不同的事件,有如下成立: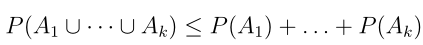
该引理的直观理解可以用下面的文氏图:
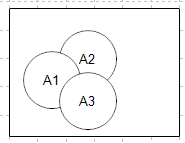
从图中显然看到P(A1UA2UA3) ≤ P(A 1 )+ P(A 2) + P(A 3 )
Hoeffding不等式
令Z 1 ,...,Z m是m个独立同分布的离散随机变量,它们服从Bernoulli(φ)分布,即P(Z i = 1) = φ, P(Z i = 0) = 1 − φ 。令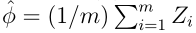
,即表示m个随机变量的算术平均,任意γ
> 0 固定,有下面的不等式成立:
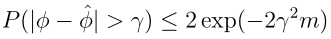
对于该不等式,下面简单的谈一下其含义。我们用高斯分布来说明(这里用高斯分布虽然不合适,因为φ是离散变量,但能够说明其含义)。先看中心极限定理的一个版本:

所以当m足够大时这里
可以看做服从正态分布,简图如下:
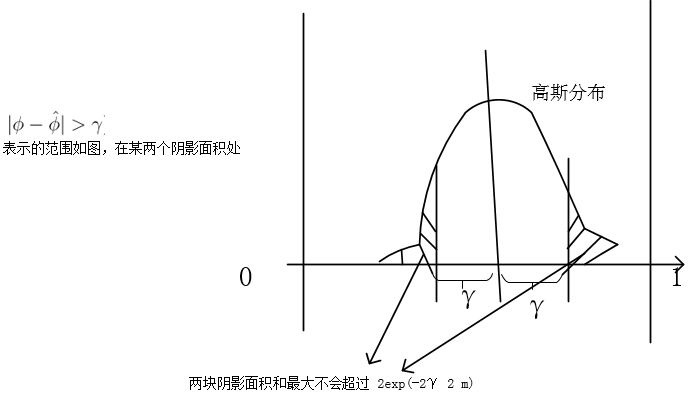
从中心极限定理看,当m增大时,算术平均的方差会变小,对应的高斯分布会收缩,这会导致两块面积的和更小,即不等式右边的值会变小,这个不等式的明显的一个意义是估计伯努利随机变量的均值时犯错误概率的上界,另外上界会随着m增长呈指数下降。待会儿会看到这个不等式是证明的关键所在。
假设类为有限的情况
我们先考虑假设类为有限的情况,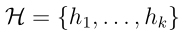
,这部分我们要证明两个内容:1.对所有h,
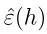
是
ε(h) 很好的近似 2.推导出一般误差的上界。随意选择一个假设记作hi,我们令随机变量
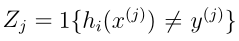
,由于样本是服从某一分布D的,且是独立同分布,那么zj之间也应该是独立同分布的,可以看到zj服从伯努利分布,且zj期望为
ε(h),也即是一般误差,那么由此我们的训练误差可以表述如下:
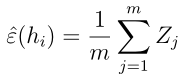
可以看到
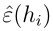
是m个随机变量zj的算术平均,zj服从伯努利分布,期望为ε(h
i ),所以直接应用Hoeffding不等式可以得到:
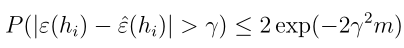
这里我们能够看到,一般误差和训练误差的差距很大时是有一个概率上界的,而当m值很大时,这个概率上界很小,即表明一般误差和训练误差差距很大的概率是很小的,也就是训练误差和一般误差很接近,这得到了我们之前的结论。但是这里我们所讨论的是针对某一个特定的假设,下面我们要证明对于所有的h ∈ H,(注意这里H仍然是有限的假设类集合)。
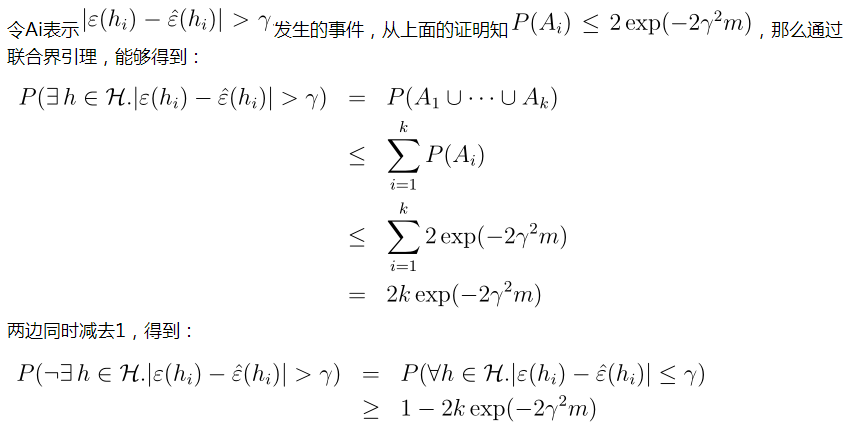
我们看一下最后推导出来的不等式的含义,对任意 h ∈ H即所有的h,得到一般误差与训练误差差距在一个 γ范围内的概率至少是 1−2k exp(−2γ 2 m),这称为一致收敛。当m很大时,对所有h,训练误差最后是向一般误差收敛的。
前面推导出来的两个不等式都是在给定m,γ求出概率界限,下面转换一下,能够得出非常有用的结论。
我们先求m,先看一个问题:给定γ,δ,如果我们要保证训练误差和一般误差在 γ范围内的概率至少是1 − δ,m至少多大? 解法很简单,只要反解出δ
= 2k exp(−2γ 2 m中的m即可,得到:
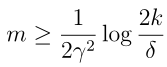
这个结论指导我们对模型的训练所选择的训练样本数,k表示假设类的个数,是前面定义的,可以看到后面一项对数函数增长是很慢的,所以即便是假设类的个数非常多,至少需要的样本数量m也不会增长多少!这个结论也叫做算法的样本复杂度。同样的,我们固定m,δ,得到γ(也称为误差界):
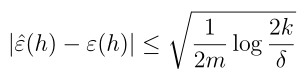
现在我们将前面的ERM与一致收敛结合起来说明一些其他性质。我们从ERM出发,即选择一个假设,使得
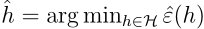
,这表示训练误差最小的假设,再令
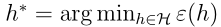
,h*表示一般误差最小的假设,它是所有假设中最好的了,我们下面要看一下这两者的关系。由一致收敛,我们知道
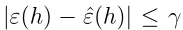
,所以有:
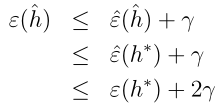
从这个不等式可以看到,ERM选出来的假设所导致的一般误差比最好的假设所导致的一般误差坏不过2γ。下面把这个结论总结为一个定理。
固定 m,δ,得到如下不等式成立:

这里用到了前面介绍的误差界,γ = √ ·,我们可以非正式的认为不等式的右边第一项是偏差,第二项是方差,那么当选择更大的假设类的集合H',使 H' ⊇ H,那么第一项肯定会降低,或者不变,k会增大,第二项会增大。即通过选取更大的假设类集合,使偏差降低了,方差增加了。这个结论帮助我们更好的量化偏差方差权衡,用一张图来说明:
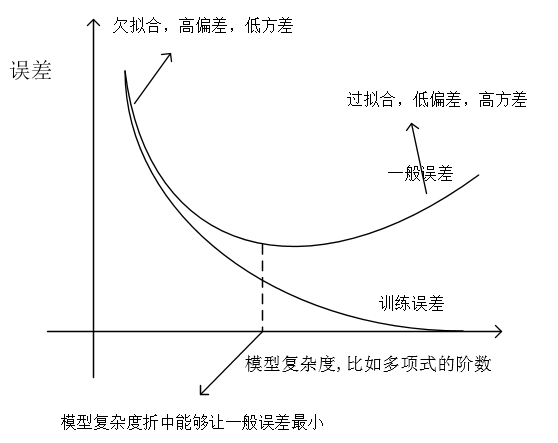
同样的,我们固定 δ,γ,使

满足,且成立的概率至少是1-δ,这个时候m满足:
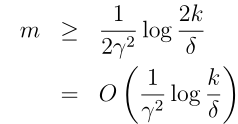
相关文章推荐
- 经验风险最小化(ERM, Empirical risk minimization)
- 经验风险最小化(ERM, Empirical risk minimization)
- 经验风险最小化(Empirical Risk Minization,ERM)
- [深度学习论文笔记][ICLR 18]mixup: BEYOND EMPIRICAL RISK MINIMIZATION
- Project Risk Management Guidelines : Managing Risk in Large Projects and Complex Procurements
- Project Risk Management
- UVA 567 - Risk
- UVaOJ 567 - Risk
- Uva 567 - Risk
- ZOJ 1221 Risk
- Paper Notes: Empirical Comparison of Algorithms for Network Community Detection
- UAV 567 - Risk --- Folyd
- uva 567 - Risk
- What is The Difference Between Risk Appetite, Risk Tolerance and Risk Threshold?
- zoj1221_Risk(多源点最短路)
- Codeforces Round #317 [AimFund Thanks-Round] (Div. 1) B. Minimization 贪心 dp
- Codeforces Round #317 [AimFund Thanks-Round] (Div. 2) D. Minimization(dp)
- HHU 冒险游戏(risk_ganme)(玛德也是血泪。。。。)
- 《Credit Risk Scorecards》读书笔记
- Financial Concepts(2): The Risk/Return Tradeoff
