逻辑回归(logistic regression)
2015-01-29 20:21
344 查看
一、 数学上的逻辑回归
前面提到,逻辑回归是判别分析方法来分类的,即 通过给定的数据x, 来直接得到其后验概率。且 它 得到的是线性分类边界。
回顾在贝叶斯准则中, 利用0-1损失进行分类时, 我们做法是 以最大的后验概率 的类 k, 来作为依据。
&space;=%5Cmathop&space;%7B%5Carg&space;%5Cmax&space;%7D%5Climits_kPr(G&space;=&space;k%7CX=x))
从而 第k 类 和 第 l 类的分类边界通过 使其概率相等来决定: 即 样本 x 在 第k 类和第l 类有相等的后验概率。
&space;=&space;Pr(G&space;=&space;l%7CX=x))
如果我们 我们对两个概率进行相除 ,并且取 log 的话 ,这样得到一个比率, 在上述情况有
%7D&space;%7BPr(G&space;=&space;l%7CX=x)%7D&space;=&space;0)
如果我们想要强制得到一个线性分类边界, 我们可以假设这个函数可以线性表示, 即
%7D&space;%7BPr(G&space;=&space;l%7CX=x)%7D&space;=&space;a_0%5E%7B(k,l)%7D&space;+&space;%5Csum&space;%5Climits_%7Bj=1%7D%5Ep%7Ba_j%5E%7B(k,l)%7D%7D&space;x_j)
逻辑回归就是在这样一个假设的的基础上得到的。 其中 对不同的两类类,有不同的系数上标(k,l), 其系数也不同。
这样看着 很容易理解, 那肯定也会有这样的疑问, 那岂不是每两类就要找一个
%7D)
, 那计算量岂不是很大 !
然而在 逻辑回归中, 我们并不用每两类 都要找一组 系数, 对于 K 类, 我们只需要进行 K-1 对配对, 找K-1 组系数就可以了。
假设开始
现在我们 有 K 类, 我们让 第K 类(可以是任何一个类)作为一个 基类, 这样 对于剩余的 K-1 类, 得到 K-1 组系数情况:
%7D&space;%7BPr(G&space;=&space;K%7CX=x)%7D&&space;=&space;%5Cbeta_%7B10%7D&space;+&space;%5Cbeta_1%5ET&space;x%5C%5C&space;log&space;%5Cfrac%7BPr(G&space;=&space;2%7CX=x)%7D&space;%7BPr(G&space;=&space;K%7CX=x)%7D&&space;=&space;%5Cbeta_%7B20%7D&space;+&space;%5Cbeta_2%5ET&space;x%5C%5C&space;&&space;%5Cvdots&space;%5C%5C&space;log&space;%5Cfrac%7BPr(G&space;=&space;K-1%7CX=x)%7D&space;%7BPr(G&space;=&space;K%7CX=x)%7D&&space;=&space;%5Cbeta_%7B(K-1)0%7D&space;+&space;%5Cbeta_%7BK-1%7D%5ET&space;x&space;%5Cend%7Balign*%7D)
我们不必找到每对的分类边界, 只要找到 每个类 和基类 的分类边界的系数。
一旦找到了 K -1 类的 log 比率, 对于任何一对(k, l) 的log 比率, 我们 就可以通过上述得到的系数组 推导出来, 比如:
这样 我们总共 参数的个数为 (K-1)×(p+1) 其中(k-1) 是 k-1 组系数, 每组中有p 维, 再添加一个常数项 1。
为了方便
4000
, 系数表示为:
)0%7D,%5Cbeta_%7BK-1%7D%5C%7D)
,
其中 后验概率的log 比率叫做 log-odds 或者logit transformations.
通过上述假设, 我们得到以下两个 后验概率公式:
=%5Cfrac&space;%7Bexp(%5Cbeta_%7Bk0%7D+%5Cbeta_k%5ET&space;x)%7D%7B1+%5Csum&space;%5Climits_%7Bl=1%7D%5E%7BK-1%7Dexp(%5Cbeta_%7Bl0%7D+%5Cbeta_l%5ET&space;x)%7D&space;%5C%5C&space;%5Cquad&space;for&space;%5C;k&space;=&space;1,2,...,K-1)
=%5Cfrac&space;%7B1%7D%7B1+%5Csum&space;%5Climits_%7Bl=1%7D%5E%7BK-1%7Dexp(%5Cbeta_%7Bl0%7D+%5Cbeta_l%5ET&space;x)%7D)
第一个公式, 可以理解 为, 将Pr(G=K|X =x) 当作单位1, 剩下的每个K-1 个与他 比, 其所占的部分是
)
, 因此对于 一个 k 类, 所占的比重为,自己的部分 比上所有加和。
第二个公式也可以这样理解, 还可以理解为 概率的总和是 1, 因此其对于K 类,其结果为 第二个公式。
因此这样就得到了, 众说 的sigmoid 函数, 具体得到就是这样了。 (来自wiki)

逻辑回归 比 线性回归相比, 它 对于 x 是非线性函数, 且概率 在0-1之间, 总和为 1。
二、 参数估计
在得到上述参数后,要计算概率,就要求解参数

,然后最大化条件似然G,
在给定x 之后,我们感兴趣的不是 X 的分布情况,而是 在哪类的概率最大。 给一点 xi, 其属于 k 类的后验概率表示为:
=Pr(G&space;=&space;k%7CX=x_i;%5Ctheta))
。
对于第一个样本x1, 它属于g1 类,则其后验概率为
)
因为样本是独立的,因此,这些N 个样本点每个类为 gi, 所以其 后验概率为。 即 联合条件似然 就是 其条件概率的乘积。
%7D)
对 参数的似然估计 即 为 log条件似然, 通过使其最大化得到。
&space;&=&space;%5Csum&space;%5Climits_%7Bi=1%7D%7BN%7D%7BlogPr(G&space;=&space;g_i%7CX=x_i)%7D%5C%5C&space;&=&space;%5Csum&space;%5Climits_%7Bi=1%7D%7BN%7D%7Blogp_%7Bg_i%7D(x_i;%5Ctheta)%7D&space;%5Cend%7Balign*%7D)
、
具体计算 过程参见 下面二分类 实战部分。
三、 二分类实战
先看二分类,对于多类是相似的情况。
对于二分类, 如果 gi = class 1, 表示为yi = 1; 如果 gi = class 2, 表示为 yi = 0. 将类标签变为0 和1 使其更加简化。
对于上式log 似然中的概率项, 用
=p(x;%5Ctheta))
=1-&space;p_1(x;%5Ctheta)=1-&space;p(x;%5Ctheta))
,因为 这两者后验概率和为1。
因为 K = 2, 我们只有一个线性多项式, 一个分类决策边界, 参数列表为

,
现在 我们在这里表示为
%5ET)
,
这是一个列向量。
现在我们要做的就是一步步, 简化, 计算, 求解
简化
对于 yi = 1, 有 gi = 1 这时其 log 似然为
&=logp_1(x;%5Cbeta)&space;%5C%5C&space;&=&space;1%5Ccdot&space;logp(x;%5Cbeta)%5C%5C&space;&=y_i&space;logp(x;%5Cbeta)&space;%5Cend%7Balign*%7D)
同样对于 yi = 0, 有 gi = 2 , 其形式为:
&=logp_2(x;%5Cbeta)&space;%5C%5C&space;&=&space;1%5Ccdot&space;log(1-p(x;%5Cbeta))%5C%5C&space;&=(1-y_i)&space;log(1-p(x;%5Cbeta))&space;%5Cend%7Balign*%7D)
因为 yi = 0 或者 1-yi = 0, 因此我们可以将以上两部分加在一起, 得到
=&space;y_i&space;logp(x;%5Cbeta)+(1-y_i)&space;log(1-p(x;%5Cbeta)))
这样做不用单独拿出来分析,对于不同的yi 都适用。 相加的log 似然形式也可得到哦简化:
&space;=&space;%5Csum&space;%5Climits_%7Bi&space;=&space;1%7D%5E%7BN%7D&space;logp_%7Bg_i%7D(x_i;%5Cbeta)&space;=&space;%5Csum&space;%5Climits_%7Bi&space;=&space;1%7D%5E%7BN%7D%5By_ilogp(x_i;%5Cbeta)+(1-y_i)log(1-p(x_i;%5Cbeta))%5D)
在
%5ET)
中
有p+1 个参数
则参数和 函数对应关系即 :
&space;%5CLeftrightarrow&space;x&space;=&space;%5Cleft(&space;%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D&space;1%5C%5C&space;%7B%5Cbegin%7Barray%7D%7B*%7B20%7D%7Bc%7D%7D&space;x_%7B,1%7D%5C%5C&space;x_%7B,2%7D%5C%5C&space;%5Cvdots&space;%5Cend%7Barray%7D%7D%5C%5C&space;x%7B,p%7D&space;%5Cend%7Barray%7D%7D&space;%5Cright))
计算
有前面的假设,哦们得到logistic 回归模型为:
&space;&=&space;Pr(G=1%7CX=x)&space;=&space;%5Cfrac&space;%7Bexp(%5Cbeta%5ETx)%7D%7B1+exp(%5Cbeta%5ETx)%7D&space;%5C%5C&space;1-p(x;%5Cbeta)&space;&=&space;Pr(G=2%7CX=x)&space;=&space;%5Cfrac&space;%7B1%7D%7B1+exp(%5Cbeta%5ETx)%7D&space;%5Cend%7Balign*%7D)
则 log-似然结果:
&space;=&space;%5Csum&space;%5Climits_%7Bi&space;=1%7D%5EN%5By_i%5Cbeta%5ETx_i-log(1+e%5E%7B%5Cbeta%5ETx_i%7D)%5D)
似然函数求参数,即最大化似然函数 ,这样对

求导j
=0,1,2...,p , 就好:
%7D%7B%5Cpartial&space;%5Cbeta_%7B1j%7D%7D&space;&=&space;%5Csum&space;%5Climits_%7Bi=1%7D%5EN%7By_ix_%7Bij%7D-%5Csum&space;%5Climits_%7Bi=1%7D%5EN&space;%5Cfrac&space;%7Bx_%7Bij%7De%5E%7B%5Cbeta%5ETx_i%7D%7D%7B1+e%5E%7B%5Cbeta%5ETx_i%7D%7D%7D&space;%5C%5C&space;&=&space;%5Csum&space;%5Climits_%7Bi=1%7D%5EN%7By_ix_%7Bij%7D%7D&space;-%5Csum&space;%5Climits_%7Bi=1%7D%5ENp(x;%5Cbeta)x_%7Bij%7D&space;%5C%5C&space;&=&space;%5Csum&space;%5Climits_%7Bi=1%7D%5ENx_%7Bij%7D(%7By_i%7D-p(x_i;%5Cbeta))&space;%5Cend%7Balign*%7D)
对上述式子进行矩阵运算即可, 其中 xi 是 列向量 yi 是标量。
为了解 p+1 个非线性等式
%7D%7B%5Cpartial&space;%5Cbeta_%7B1j%7D%7D&space;=&space;0,&space;%5C;&space;j&space;=&space;0,1..p)
,
我们利用 Newton迭代法进行求解:
牛顿迭代法需要 二阶导数 Hessian 矩阵 :
%7D%7B%5Cpartial&space;%5Cbeta%5Cpartial&space;%5Cbeta%5ET%7D&space;=&space;-%5Csum&space;%5Climits_%7Bi=1%7D%5EN&space;%7Bx_ix_i%5ET&space;p(x_i;%5Cbeta)(1-p(x_i;%5Cbeta))%7D)
在第 j 行 第 n 列的情况如下:
%7D%7B%5Cpartial&space;%5Cbeta_%7B1j%7D%5Cpartial&space;%5Cbeta_%7B1n%7D%7D&space;%5C%5C&space;&=&space;-&space;%5Csum&space;%5Climits_%7Bi=1%7D%5EN&space;%5Cfrac&space;%7B(1+e%5E%7B%5Cbeta%5ETx_i%7D)e%5E%7B%5Cbeta%5ETx_i%7Dx_%7Bij%7Dx_%7Bin%7D&space;-&space;(e%5E%7B%5Cbeta%5ETx_i%7D)%5E2%7Bx_%7Bij%7Dx_%7Bin%7D%7D%7D&space;%7B(1+e%5E%7B%5Cbeta%5ETx_i%7D)%5E2%7D%5C%5C&space;&=&space;-&space;%5Csum&space;%5Climits_%7Bi=1%7D%5EN&space;x_%7Bij%7Dx_%7Bin%7D&space;p(x_i;%5Cbeta)&space;-&space;x_%7Bij%7Dx_%7Bin%7D&space;p(x_i;%5Cbeta)%5E2&space;%5C%5C&space;&=&space;-%5Csum&space;%5Climits_%7Bi=1%7D%5EN&space;%7Bx_ix_i%5ET&space;p(x_i;%5Cbeta)(1-p(x_i;%5Cbeta))%7D)
这样我们利用牛顿迭代,不断更新参数:
%7D%7B%5Cpartial&space;%5Cbeta%5Cpartial&space;%5Cbeta%5ET%7D)%5E%7B-1%7D&space;%5Cfrac&space;%7B%5Cpartial&space;l(%5Cbeta)%7D%7B%5Cpartial&space;%5Cbeta%7D)
这样,如果给了一个旧的参数

,
通过得到Hessian 矩阵 与 一阶导数的乘积, 这样就可对

, 进行更新得到

.
求解
迭代的过程可用以下矩阵形式来进行:
y: 为 yi 的列向量来表示
X: 为输入矩阵 N×(p+1) 表示
p: 拟合概率的N维向量, 第 i 个数据样本表示为
)
W: N×N为对角权重矩阵, 第 i 个对角元素为
(1-p(x_i;%5Cbeta%5E%7Bold%7D)))
在上述基础上构建一阶导数表示为:
%7D%7B%5Cpartial&space;%5Cbeta%7D&space;=&space;X%5ET(y-p))
Hessian 矩阵表示为 :
%7D%7B%5Cpartial&space;%5Cbeta&space;%5Cpartial&space;%5Cbeta%5ET%7D&space;=&space;-X%5ETWX)
因而牛顿步更新之后为:
%5E%7B-1%7DX%5ET(y-p)&space;%5C%5C&space;&=&space;(X%5ETWX)%5E%7B-1%7DX%5ETW(X%5Cbeta%5E%7Bold%7D+W%5E%7B-1%7D&space;(y-p))%5C%5C&space;&=(X%5ETWX)%5E%7B-1%7DX%5ETWz&space;%5Cend%7Balign*%7D&space;%5C%5C&space;where&space;~~&space;z&space;=&space;X%5Cbeta%5E%7Bold%7D+W%5E%7B-1%7D&space;(y-p))
如果 z 看作是 X 输入下的一个响应 输出, 则

求解过程是一个带权的最小二乘问题:
%5ETW(z-X%5Cbeta)%7D)
回想想线性回归中的最小二乘是去解:
%5ET(z-X%5Cbeta)%7D)
z 做为一个 适应性 的响应 , 这就是 IRLS(iteratively reweighted least squares) 算法。
其伪代码算法过程为:

因为在这里要求 W 的逆 进行逆 运算, 因此计算效率有所下降, 这里 引入了修改后的 高效运算方法,两者是等价的。

这里在计算时,要注意运算第三步,对每个求概率是 都是求p ,没有求 1-p。
c++ 代码算法实现:
利用了 男性、女性 由身高体重 进行区分的分类, 总共210 个样本点, 且最终训练数据误差率为11.9048% (后续可采用交叉验证来试验)。
最终结果: 收敛,迭代次数, 最终更新参数, 误差率。

并且利用 opencv 将结果进行了显示:

分类来看,效果还是不错的。
正则化(l2)逻辑回归

即用MAP代替 MLE, 并且计算 是 在其基础上修改 目标函数, 梯度和 Hessian 矩阵。
贝叶斯逻辑回归
逻辑回归我们并没有考虑先验,如果加入先验的清况, 这时, 我们希望 逻辑回归是高斯分布的, 且其先验形式为
=N(w%7C0,V_0))
,
这样其后验概率也是高斯的, 即
=N(w%7C%5Chat&space;w,H%5E%7B-1%7D))
整个近似的过程是 Laplace 近似: 因为我们想要后验是 正太分布, 但是 逻辑回归的 估计式子是没有相应的共轭先验与其相对应的, 这样,我们近似过程如下。
假设 其后验 为
=%5Cfrac&space;%7B1%7D%7BZ%7De%5E%7B-E(%5Ctheta)%7D)
其中
)
是能量函数,等于负log非正太log
后验,
&space;=&space;-logp(%5Ctheta,D))
,
其中 z = p(D) 是正太常值。 这样我们对
)
进行 Taylor 级数展开:
&space;%5Capprox&space;E(%5Ctheta%5E*)&space;+(%5Ctheta-%5Ctheta%5E*)g+%5Cfrac&space;%7B1%7D%7B2%7D(%5Ctheta-%5Ctheta%5E*)%5ETH(%5Ctheta-%5Ctheta%5E*))
这样我们取 在
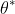
处取得 最小能量值,且其
g 梯度为0 ,这样 我们可得到正太的后验分布,其中:
&space;&&space;%5Capprox&space;%5Cfrac%7B1%7D%7BZ%7De%5E%7B-E(%5Ctheta%5E*)%7D&space;exp%5B-%5Cfrac%7B1%7D%7B2%7D(%5Ctheta-%5Ctheta%5E*)%5ETH(%5Ctheta-%5Ctheta%5E*)%5D&space;=&space;N(%5Ctheta%7C%5Ctheta%5E*,&space;H%5E%7B-1%7D)%5C%5C&space;Z&space;=&space;p(D)&space;&&space;%5Capprox&space;%5Cint&space;%5Chat&space;p(%5Ctheta%7CD)&space;d%5Ctheta&space;=&space;e%5E%7B-E(%5Ctheta%5E*)%7D(2%5Cpi)%5E%7BD/2%7D%7CH%7C%5E%7B-%5Cfrac%7B1%7D%7B2%7D%7D)
这样就可得到想要的高斯分布。
另 《Bayesian Data Analysis》介绍 对于 weakly information of prior 可考虑用 strdent-分布,然后用EM 进行参数的估计。也可进行贝叶斯经验运用。
四 、多类情况
多类的情况, 是与二类的情况相类似, 计算量增加了许多。 参见 https://onlinecourses.science.psu.edu/stat557/node/56
五、总结
通过 直接的判别分析, 不利用先验就可进行分类,并且在直接分类上,如果对模型未知时往往到达不错的 效果。 并且可以利用 L2正则化 进行不理想情况的修正; 在贝叶斯模型中, 加入先验时,可以利用近似方法来得到想要的模型。
六、参考资料
1. https://onlinecourses.science.psu.edu/stat557/node/52
2. 《Machine Learning A Probabilistic Perspective》 第八章 logistic regression
3. 《Bayesian Data Analysis》
前面提到,逻辑回归是判别分析方法来分类的,即 通过给定的数据x, 来直接得到其后验概率。且 它 得到的是线性分类边界。
回顾在贝叶斯准则中, 利用0-1损失进行分类时, 我们做法是 以最大的后验概率 的类 k, 来作为依据。
从而 第k 类 和 第 l 类的分类边界通过 使其概率相等来决定: 即 样本 x 在 第k 类和第l 类有相等的后验概率。
如果我们 我们对两个概率进行相除 ,并且取 log 的话 ,这样得到一个比率, 在上述情况有
如果我们想要强制得到一个线性分类边界, 我们可以假设这个函数可以线性表示, 即
逻辑回归就是在这样一个假设的的基础上得到的。 其中 对不同的两类类,有不同的系数上标(k,l), 其系数也不同。
这样看着 很容易理解, 那肯定也会有这样的疑问, 那岂不是每两类就要找一个
, 那计算量岂不是很大 !
然而在 逻辑回归中, 我们并不用每两类 都要找一组 系数, 对于 K 类, 我们只需要进行 K-1 对配对, 找K-1 组系数就可以了。
假设开始
现在我们 有 K 类, 我们让 第K 类(可以是任何一个类)作为一个 基类, 这样 对于剩余的 K-1 类, 得到 K-1 组系数情况:
我们不必找到每对的分类边界, 只要找到 每个类 和基类 的分类边界的系数。
一旦找到了 K -1 类的 log 比率, 对于任何一对(k, l) 的log 比率, 我们 就可以通过上述得到的系数组 推导出来, 比如:
这样 我们总共 参数的个数为 (K-1)×(p+1) 其中(k-1) 是 k-1 组系数, 每组中有p 维, 再添加一个常数项 1。
为了方便
4000
, 系数表示为:
,
其中 后验概率的log 比率叫做 log-odds 或者logit transformations.
通过上述假设, 我们得到以下两个 后验概率公式:
第一个公式, 可以理解 为, 将Pr(G=K|X =x) 当作单位1, 剩下的每个K-1 个与他 比, 其所占的部分是
, 因此对于 一个 k 类, 所占的比重为,自己的部分 比上所有加和。
第二个公式也可以这样理解, 还可以理解为 概率的总和是 1, 因此其对于K 类,其结果为 第二个公式。
因此这样就得到了, 众说 的sigmoid 函数, 具体得到就是这样了。 (来自wiki)

逻辑回归 比 线性回归相比, 它 对于 x 是非线性函数, 且概率 在0-1之间, 总和为 1。
二、 参数估计
在得到上述参数后,要计算概率,就要求解参数
,然后最大化条件似然G,
在给定x 之后,我们感兴趣的不是 X 的分布情况,而是 在哪类的概率最大。 给一点 xi, 其属于 k 类的后验概率表示为:
。
对于第一个样本x1, 它属于g1 类,则其后验概率为
因为样本是独立的,因此,这些N 个样本点每个类为 gi, 所以其 后验概率为。 即 联合条件似然 就是 其条件概率的乘积。
对 参数的似然估计 即 为 log条件似然, 通过使其最大化得到。
、
具体计算 过程参见 下面二分类 实战部分。
三、 二分类实战
先看二分类,对于多类是相似的情况。
对于二分类, 如果 gi = class 1, 表示为yi = 1; 如果 gi = class 2, 表示为 yi = 0. 将类标签变为0 和1 使其更加简化。
对于上式log 似然中的概率项, 用
,因为 这两者后验概率和为1。
因为 K = 2, 我们只有一个线性多项式, 一个分类决策边界, 参数列表为
,
现在 我们在这里表示为
,
这是一个列向量。
现在我们要做的就是一步步, 简化, 计算, 求解
简化
对于 yi = 1, 有 gi = 1 这时其 log 似然为
同样对于 yi = 0, 有 gi = 2 , 其形式为:
因为 yi = 0 或者 1-yi = 0, 因此我们可以将以上两部分加在一起, 得到
这样做不用单独拿出来分析,对于不同的yi 都适用。 相加的log 似然形式也可得到哦简化:
在
中
有p+1 个参数
则参数和 函数对应关系即 :
计算
有前面的假设,哦们得到logistic 回归模型为:
则 log-似然结果:
似然函数求参数,即最大化似然函数 ,这样对
求导j
=0,1,2...,p , 就好:
对上述式子进行矩阵运算即可, 其中 xi 是 列向量 yi 是标量。
为了解 p+1 个非线性等式
,
我们利用 Newton迭代法进行求解:
牛顿迭代法需要 二阶导数 Hessian 矩阵 :
在第 j 行 第 n 列的情况如下:
这样我们利用牛顿迭代,不断更新参数:
这样,如果给了一个旧的参数
,
通过得到Hessian 矩阵 与 一阶导数的乘积, 这样就可对
, 进行更新得到
.
求解
迭代的过程可用以下矩阵形式来进行:
y: 为 yi 的列向量来表示
X: 为输入矩阵 N×(p+1) 表示
p: 拟合概率的N维向量, 第 i 个数据样本表示为
W: N×N为对角权重矩阵, 第 i 个对角元素为
在上述基础上构建一阶导数表示为:
Hessian 矩阵表示为 :
因而牛顿步更新之后为:
如果 z 看作是 X 输入下的一个响应 输出, 则
求解过程是一个带权的最小二乘问题:
回想想线性回归中的最小二乘是去解:
z 做为一个 适应性 的响应 , 这就是 IRLS(iteratively reweighted least squares) 算法。
其伪代码算法过程为:

因为在这里要求 W 的逆 进行逆 运算, 因此计算效率有所下降, 这里 引入了修改后的 高效运算方法,两者是等价的。

这里在计算时,要注意运算第三步,对每个求概率是 都是求p ,没有求 1-p。
c++ 代码算法实现:
利用了 男性、女性 由身高体重 进行区分的分类, 总共210 个样本点, 且最终训练数据误差率为11.9048% (后续可采用交叉验证来试验)。
/*
@Newton-Method :
@iteratively reweighted least squares
@x_train : train sample of data
@y_train : train result of data
@weight : the train weight result.
@use the Computational Efficiency
@use the matrix term to express the process
*/
void IterReweightedLS(Matrix &x_train, Matrix &y_train, Matrix &weight)
{
//change the y as 1->1, 2->0
for (int row = 0; row < y_train.GetMatrixRow(); row++)
{
if (y_train.GetMatrixValue(row, 0) == 2.0)
y_train.SetMatrixOnePosition(row, 0, 0.0);
}
//use the pro-resadual to judge weather converge
Matrix odl_pro_use_for_converge(y_train.GetMatrixRow(), y_train.GetMatrixCol());
odl_pro_use_for_converge.SetMatrixAllOne();
odl_pro_use_for_converge = odl_pro_use_for_converge.MatrixMultiNumPerRow(-1, 0);
int iter_count = IterNumber;
while (iter_count--)
{
// use the matrix to express the culculate
// the probability of the sigmoid express form
Matrix temp(x_train.GetMatrixRow(), 1);
Matrix probability(y_train.GetMatrixRow(), y_train.GetMatrixCol());
temp = x_train.MatrixMulti(weight);
//another thing the probability all be exp(xw)/exp(xw)+1, because we have connected it all together
for (int pro_row = 0; pro_row < y_train.GetMatrixRow(); pro_row++)
{
double pro = sigmoid(temp.GetMatrixValue(pro_row, 0));
probability.SetMatrixOnePosition(pro_row, 0, pro);
}
//the W of diagonal matrix use the value p*(1-p)
Matrix W(y_train.GetMatrixRow(), y_train.GetMatrixRow());
W.SetMatrixAllZero();
Matrix one_cut_pro(probability.GetMatrixRow(),1);
one_cut_pro.SetMatrixAllOne();
Matrix pro_multi_one_cut_pro(probability);
pro_multi_one_cut_pro = probability.MatrixPointMlutiMatrix((one_cut_pro.MatrixCut(probability)));
W.SetDialogUsVector(pro_multi_one_cut_pro);
//x_hat for culmulate efficient
// remember the iter pre and after.
Matrix x_hat = x_train;
for (int row = 0; row < x_train.GetMatrixRow(); row++)
{
x_hat = x_hat.MatrixMultiNumPerRow(pro_multi_one_cut_pro.GetMatrixValue(row, 0), row);
}
//culmulate the (x^T x_hat)^(-1)*x^T*(Y-P)
// first LUP factorization
// and then culmulate the parameter w_redisual
Matrix x_trans = x_train.MatrixTrans();
Matrix x_factorization = x_trans.MatrixMulti(x_hat);
Matrix right_value = x_trans.MatrixMulti(y_train.MatrixCut(probability));
//(x^T x_hat)^(-1) if the x_factorization
//use the lup factorization to culmulate
LUPFactorization matrix_factor(x_factorization);
matrix_factor.Factorization();
right_value = (matrix_factor.GetP()).MatrixMulti(right_value);
//use the l-down triangle and u-up triange to compute it
Matrix intermediray_vector = right_value.MatrixDivideDownTriangle(matrix_factor.GetL());
Matrix terminal_vector = intermediray_vector.MatrixDivideUpTriangle(matrix_factor.GetU());
weight = weight.MatrixPlus(terminal_vector);
Matrix pro_redasual = probability.MatrixCut(odl_pro_use_for_converge);
//whether converged
double sum_pro_resudal = pro_redasual.VectorL1Norm();
//cout << sum_pro_resudal << endl;
if (sum_pro_resudal < (NumberSamble * Epsilon))
{
cout << "the gradient l2 norm is: " << sum_pro_resudal << endl;
cout << "the iter number is: " << IterNumber - iter_count << endl;
weight.ShowMatrix();
break;
}
odl_pro_use_for_converge = probability;
}
}最终结果: 收敛,迭代次数, 最终更新参数, 误差率。

并且利用 opencv 将结果进行了显示:

分类来看,效果还是不错的。
正则化(l2)逻辑回归

即用MAP代替 MLE, 并且计算 是 在其基础上修改 目标函数, 梯度和 Hessian 矩阵。
贝叶斯逻辑回归
逻辑回归我们并没有考虑先验,如果加入先验的清况, 这时, 我们希望 逻辑回归是高斯分布的, 且其先验形式为
,
这样其后验概率也是高斯的, 即
整个近似的过程是 Laplace 近似: 因为我们想要后验是 正太分布, 但是 逻辑回归的 估计式子是没有相应的共轭先验与其相对应的, 这样,我们近似过程如下。
假设 其后验 为
其中
是能量函数,等于负log非正太log
后验,
,
其中 z = p(D) 是正太常值。 这样我们对
进行 Taylor 级数展开:
这样我们取 在
处取得 最小能量值,且其
g 梯度为0 ,这样 我们可得到正太的后验分布,其中:
这样就可得到想要的高斯分布。
另 《Bayesian Data Analysis》介绍 对于 weakly information of prior 可考虑用 strdent-分布,然后用EM 进行参数的估计。也可进行贝叶斯经验运用。
四 、多类情况
多类的情况, 是与二类的情况相类似, 计算量增加了许多。 参见 https://onlinecourses.science.psu.edu/stat557/node/56
五、总结
通过 直接的判别分析, 不利用先验就可进行分类,并且在直接分类上,如果对模型未知时往往到达不错的 效果。 并且可以利用 L2正则化 进行不理想情况的修正; 在贝叶斯模型中, 加入先验时,可以利用近似方法来得到想要的模型。
六、参考资料
1. https://onlinecourses.science.psu.edu/stat557/node/52
2. 《Machine Learning A Probabilistic Perspective》 第八章 logistic regression
3. 《Bayesian Data Analysis》
相关文章推荐
- 逻辑回归在个人信用评估模型上的运用
- 极大似然 S函数 逻辑回归 具体案例 学习笔记
- 分类和回归(三)-逻辑回归
- 机器学习笔记(一)逻辑回归与多项逻辑回归
- 分类算法之逻辑回归
- 逻辑回归python实现实例
- 逻辑回归的概率函数为什么要用sigmoid函数?
- 机器学习_逻辑回归costFunction表示形式
- 【转载】Logistic regression (逻辑回归) 概述
- stanford coursera 机器学习编程作业 exercise 3(逻辑回归实现多分类问题)
- “逻辑回归” 和 "线性回归" 的关系
- 机器学习算法与Python实践(2) - 逻辑回归
- 神经网络-逻辑回归
- 对线性回归、逻辑回归、各种回归的概念学习
- mllib逻辑回归LogisticRegressionWithLBFGS LogisticRegressionModel源码分析
- 逻辑回归与softmax回归
- Spark LogisticRegression 逻辑回归之建模
- gbdt与逻辑回归融合
- 在大数据回归模型方法的培训逻辑
- Andrew机器学习课程笔记(1)——梯度下降、逻辑回归
