椭圆的生成算法
2014-11-27 10:06
525 查看
椭圆和直线、圆一样,是图形学领域中的一种常见图元,椭圆的生成算法(光栅转换算法)也是图形学软件中最常见的生成算法之一。在平面解析几何中,椭圆的方程可以描述为(x – x0)2 / a2+ (y – y0)2 / b2 = 1,其中(x0,
y0)是圆心坐标,a和b是椭圆的长短轴,特别的,当(x0, y0)就是坐标中心点时,椭圆方程可以简化为x2
/ a2 + y2 / b2 = 1。在计算机图形学中,椭圆图形也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的椭圆的生成,对于中心不是原点的椭圆,可以通过坐标的平移变换获得相应位置的椭圆。
在进行扫描转换之前,需要了解一下椭圆的对称性,如图(1)所示:
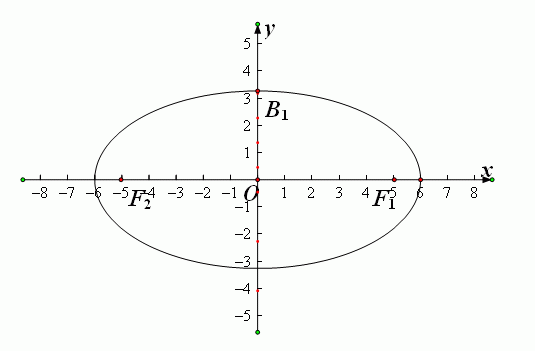
图(1)椭圆的对称性
中心在原点。焦点在坐标轴上的标准椭圆具有X轴对称、Y轴对称和原点对称特性,已知椭圆上第一象限的P点坐标是(x,
y),则椭圆在另外三个象限的对称点分别是(x, -y)、(-x, y)和(-x, -y)。因此,只要画出第一象限的四分之一椭圆,就可以利用这三个对称性得到整个椭圆。
在光栅设备上输出椭圆有很多种方法,可以根据直角平面坐标方程直接求解点坐标,yekeyii利用极坐标方程求解,但是因为涉及到浮点数取整,效果都不好,一般都不使用直接求解的方式。本文就介绍几种计算机图形学中两种比较常用的椭圆生成方法:中点画椭圆算法和Bresenham椭圆生成算法。
1、
中点画椭圆法
中点在坐标原点,焦点在坐标轴上(轴对齐)的椭圆的平面集合方程是:
x2 / a2 + y2 / b2
= 1,也可以转化为如下非参数化方程形式:
F(x, y) = b2x2 + a2y2
- a2b2 = 0 (方程 1)
无论是中点画线算法、中点画圆算法还是本节要介绍的中点画椭圆算法,对选择x方向像素Δ增量还是y方向像素Δ增量都是很敏感的。举个例子,如果某段圆弧上,x方向上增量+1个像素时,y方向上的增量如果
< 1,则比较适合用中点算法,如果y方向上的增量 > 1,就会产生一些跳跃的点,最后生成的光栅位图圆弧会有一些突变的点,看起来好像不在圆弧上。因此,对于中点画圆弧算法,要区分出椭圆弧上哪段Δx增量变化显著,哪段Δy增量变化显著,然后区别对待。由于椭圆的对称性,我们只考虑第一象限的椭圆圆弧,如图(2)所示:
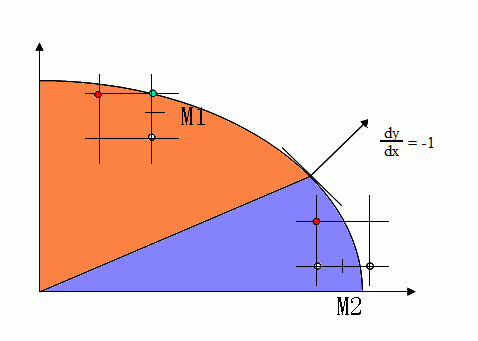
图(2)第一象限椭圆弧示意图
定义椭圆弧上某点的切线法向量N如下:

对方程1分别求x偏导和y偏导,最后得到椭圆弧上(x,y)点处的法向量是(2b2x,
2a2y)。dy/dx = -1的点是椭圆弧上的分界点。此点之上的部分(橙褐色部分)椭圆弧法向量的y分量比较大,即:2b2(x
+ 1) < 2a2(y – 0.5);此点之下的部分(蓝紫色部分)椭圆弧法向量的x分量比较大,即:2b2(x + 1) > 2a2(y
– 0.5)。
对于图(2)中橙褐色标识的上部区域,y方向每变化1个单位,x方向变化大于一个单位,因此中点算法需要沿着x方向步进画点,x每次增量加1,求y的值。同理,对于图(2)中蓝紫色标识的下部区域,中点算法沿着y方向反向步进,y每次减1,求x的值。先来讨论上部区域椭圆弧的生成,如图(3)所示:

图(3)中点画椭圆算法对上部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点右边的P1(xi+1,
yi)点或右下方的P2(xi+1, yi-1)点,取舍的方法取决于判别式di,di的定义如下:
di = F(xi+1, yi-0.5) = b2(xi+1)2
+ a2(yi-0.5)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P1为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2
+ a2(yi-0.5)2 – a2b2
= di + b2(2xi + 3)
计算出di的增量是b2(2xi
+ 3)。同理,若di >= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P2为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2
+ a2(yi-1.5)2 – a2b2
= d1 + b2(2xi+3) + a2(-2yi+2)
计算出di的增量是b2(2xi+3)+a2(-2yi+2)。计算di的增量的目的是减少计算量,提高算法效率,每次判断一个点时,不必完整的计算判别式di,只需在上一次计算出的判别式上增加一个增量即可。
接下来继续讨论下部区域椭圆弧的生成,如图(4)所示:

图(4)中点画椭圆算法对下部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点左下方的P1(xi
-1, yi-1)点或下方的P2(xi, yi-1)点,取舍的方法同样取决于判别式di,di的定义如下:
di = F(xi+0.5, yi-1) = b2(xi+0.5)2
+ a2(yi-1)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P2为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+1.5)2
+ a2(yi-2)2 – a2b2 =
di + b2(2xi+2)+a2(-2yi+3)
计算出di的增量是b2(2xi+2)+a2(-2yi+3)。同理,若di
>= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P1为下一个像素点。此时xi+1
= xi,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+0.5)2
+ a2(yi-2)2 – a2b2 =
d1 + a2(-2yi+3)
计算出di的增量是a2(-2yi+3)。
中点画椭圆算法从(0, b)点开始,第一个中点是(1, b – 0.5),判别式d的初始值是:
d0 = F(1, b–0.5) = b2 + a2(-b+0.25)
上部区域生成算法的循环终止条件是:2b2(x + 1) >= 2a2(y – 0.5),下部区域的循环终止条件是y
= 0,至此,中点画椭圆算法就可以完整给出了:
EllipsePlot()函数利用椭圆的三个对称性,一次完成四个对称点的绘制,因为简单,此处就不再列出代码。
2、 Bresenham算法
中点画椭圆法中,计算判别式d使用了浮点运算,影响了椭圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画椭圆法进行了多种改进,提出了很多种中点生成椭圆的整数型算法,Bresenham椭圆生成算法就是其中之一。
在生成椭圆上部区域时,以x轴为步进方向,如图(5-a)所示:
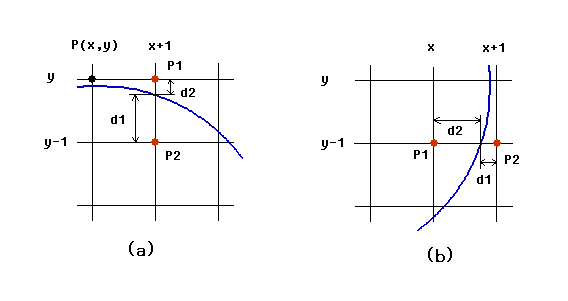
图(5)Bresenham椭圆生成算法判别式
x每步进一个单位,就需要在判断y保持不变还是也步进减1,bresenham算法定义判别式为:
D = d1 – d2
如果D < 0,则取P1为下一个点,否则,取P2为下一个点。采用判别式D,避免了中点算法因y-0.5而引入的浮点运算,使得判别式规约为全整数运算,算法效率得到了很大的提升。根据椭圆方程,可以计算出d1和d2分别是:
d1 = a2(yi2 – y2)
d2 = a2(y2 – yi+12)
以(0, b)作为椭圆上部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di + 2b2(2xi
+ 3) (Di < 0)
Di+1 = Di + 2b2(2xi
+ 3) – 4a2(yi - 1) (Di >= 0)
D0 = 2b2 – 2a2b + a2
在生成椭圆下部区域时,以y轴为步进方向,如图(5-b)所示,y每步进减一个单位,就需要在判断x保持不变还是步进加一个单位,对于下部区域,计算出d1和d2分别是:
d1 = b2(xi+12 – x2)
d2 = b2(x2 – xi2)
以(xp, yp)作为椭圆下部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di – 4a2(yi
- 1) + 2a2 (Di < 0)
Di+1 = Di + 2b2(xi
+ 1) – 4a2(y - 1) + 2a2 + b2 (Di >= 0)
D0 = b2(xp + 1)2
+b2xp2 - 2a2b2 + 2a2(yp
- 1)2
根据以上分析,Bresenham椭圆生成算法的实现就比较简单了:
总结一下,本文介绍了两种计算机图形学中常见的椭圆生成算法,实际上还有很多种改进算法,包括提高效率,引入反走样技术等等,但那已经不是本文的重点,能把算法的基本原理讲清楚才是本文的目的。
参考资料:
【1】计算几何:算法设计与分析周培德
清华大学出版社 2005年
【2】计算几何:算法与应用德贝尔赫(邓俊辉译)
清华大学出版社 2005年
【3】计算机图形学孙家广、杨常贵清华大学出版社 1995年
椭圆的中点生成算法
第二种方法
椭圆中点生成算法
椭圆对称性质原理:
(1)圆是满足x轴对称的,这样只需要计算原来的1/2点的位置;
(2)圆是满足y轴对称的,这样只需要计算原来的1/2点的位置;
通过上面分析可以得到实际上我们计算椭圆生成时候,只需要计算1/4个椭圆就可以实现对于所有点的生成了。
例如:分析出来目标点(x,y)必然存在(x,-y),(-x,y),(-x,-y)的另外3个点。关于中心画圆算法,通过计算x
= 0到 y = 0
的1/4椭圆的范围,然后通过对称原理得到其他3/4个点的信息。(R2表示椭圆厂轴的半径)
椭圆中点生成算法是将椭圆在第一象限中分为两个部分:
(1)对于斜率绝对值小于1的区域内在x方向取单位量;
(2)对于斜率绝对值大于1的区域内在y方向取单位量;
斜率可以通过椭圆的标准方程中获得为
K = - (ry*ry)*x/(rx*rx)*y;
这里中点椭圆生成算法同样和Bresenham算法有很多相似之处,同样有一个决定下一个位置的关键值P来做权衡处理。在中点画椭圆算法中,通过平移的方法将假设圆心在坐标原点,然后计算,最后再平移到真实原心位置。
中点椭圆算法内容:
1,输入椭圆的两个半径r1和r2,并且输入椭圆的圆心。设置初始点(x0,y0)的位置为(0,r2);
2,计算区域1中央决策参数的初始值
p = ry*ry - rx*rx*ry + 1/4*(rx*rx);
3,在区域1中的每个Xn为止,从n
= 0 开始,直到|K|(斜率)小于-1时后结束;
(1)如果p < 0
,绘制下一个点(x+1,y),并且计算
p = p + r2*r2*(3+2*x);
(2)如果P >=0 ,绘制下一个点(x+1,y-1),并且计算
p = p + r2*r2*(3+2*point.x) - 2*r1*r1*(y-1)
4,设置新的参数初始值;
p = ry*ry(X0+1/2)*(X0+1/2) + rx*rx*(Y0-1) - rx*rx*ry*ry;
5,在区域2中的每个Yn为止,从n
= 0开始,直到y = 0时结束。
(1)如果P>0的情况下,下一个目标点为(x,y-1),并且计算
p = p - 2rx*rx*(Yn+1) + rx*rx;
(2)如果p<=0的情况下,下一个目标点为(x+1,y-1),并且计算
p = p - 2rx*rx*Y(n+1) + 2ry*ry*(Xn+1)+rx*rx;
6,更具对称性原理计算其他3个象限的坐标。
7,急速拿出中心位置在(x1,y1)的位置
x = x + x1;
y = y + y1;
实例代码:
#include <iostream>
#include <math.h>
using namespace std;
struct Point{
int x;
int y;
};
void PointsEllipse(int x,int y,int r1,int r2){
Point point;
int p ;//参数
int k ; //斜率
point.x = 0;
point.y = r2;
//
计算区域1中央决策参数的初始值
p =
r2*r2 - r1*r1*r2 + 1/4*(r1*r1);
while( point.x < point.y){
if( p < 0){
point.x ++;
p = p + r2*r2*(3+2*point.x);
}
else{
point.x++;
point.y--;
p = p + r2*r2*(3+2*point.x) - 2*r1*r1*(point.y-1) ;
}
temp.x = point.x + x;
temp.y = point.y + y;
printf("Point X:%d Y:%d\r\n",temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",temp.x,-temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,-temp.y);
}
p = r2*r2*(0+1/2)*(0+1/2) + r1*r1*(r1-1)*(r1-1) - r1*r1*r2*r2;
while(point.y > 0){
if(p > 0){
point.y--;
p = p - 2*r1*r1*point.y - 2*r1*r1 + r1*r1;
}
else{
point.y--;
point.x++;
p = p - 2*r1*r1*point.y - 2*r1*r1 + r1*r1 + 2*r2*r2*point.x + 2*r2*r2 ;
}
temp.x = point.x + x;
temp.y = point.y + y;
printf("Point X:%d Y:%d\r\n",temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",temp.x,-temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,-temp.y);
}
}
y0)是圆心坐标,a和b是椭圆的长短轴,特别的,当(x0, y0)就是坐标中心点时,椭圆方程可以简化为x2
/ a2 + y2 / b2 = 1。在计算机图形学中,椭圆图形也存在在点阵输出设备上显示或输出的问题,因此也需要一套光栅扫描转换算法。为了简化,我们先考虑圆心在原点的椭圆的生成,对于中心不是原点的椭圆,可以通过坐标的平移变换获得相应位置的椭圆。
在进行扫描转换之前,需要了解一下椭圆的对称性,如图(1)所示:

图(1)椭圆的对称性
中心在原点。焦点在坐标轴上的标准椭圆具有X轴对称、Y轴对称和原点对称特性,已知椭圆上第一象限的P点坐标是(x,
y),则椭圆在另外三个象限的对称点分别是(x, -y)、(-x, y)和(-x, -y)。因此,只要画出第一象限的四分之一椭圆,就可以利用这三个对称性得到整个椭圆。
在光栅设备上输出椭圆有很多种方法,可以根据直角平面坐标方程直接求解点坐标,yekeyii利用极坐标方程求解,但是因为涉及到浮点数取整,效果都不好,一般都不使用直接求解的方式。本文就介绍几种计算机图形学中两种比较常用的椭圆生成方法:中点画椭圆算法和Bresenham椭圆生成算法。
1、
中点画椭圆法
中点在坐标原点,焦点在坐标轴上(轴对齐)的椭圆的平面集合方程是:
x2 / a2 + y2 / b2
= 1,也可以转化为如下非参数化方程形式:
F(x, y) = b2x2 + a2y2
- a2b2 = 0 (方程 1)
无论是中点画线算法、中点画圆算法还是本节要介绍的中点画椭圆算法,对选择x方向像素Δ增量还是y方向像素Δ增量都是很敏感的。举个例子,如果某段圆弧上,x方向上增量+1个像素时,y方向上的增量如果
< 1,则比较适合用中点算法,如果y方向上的增量 > 1,就会产生一些跳跃的点,最后生成的光栅位图圆弧会有一些突变的点,看起来好像不在圆弧上。因此,对于中点画圆弧算法,要区分出椭圆弧上哪段Δx增量变化显著,哪段Δy增量变化显著,然后区别对待。由于椭圆的对称性,我们只考虑第一象限的椭圆圆弧,如图(2)所示:

图(2)第一象限椭圆弧示意图
定义椭圆弧上某点的切线法向量N如下:

对方程1分别求x偏导和y偏导,最后得到椭圆弧上(x,y)点处的法向量是(2b2x,
2a2y)。dy/dx = -1的点是椭圆弧上的分界点。此点之上的部分(橙褐色部分)椭圆弧法向量的y分量比较大,即:2b2(x
+ 1) < 2a2(y – 0.5);此点之下的部分(蓝紫色部分)椭圆弧法向量的x分量比较大,即:2b2(x + 1) > 2a2(y
– 0.5)。
对于图(2)中橙褐色标识的上部区域,y方向每变化1个单位,x方向变化大于一个单位,因此中点算法需要沿着x方向步进画点,x每次增量加1,求y的值。同理,对于图(2)中蓝紫色标识的下部区域,中点算法沿着y方向反向步进,y每次减1,求x的值。先来讨论上部区域椭圆弧的生成,如图(3)所示:

图(3)中点画椭圆算法对上部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点右边的P1(xi+1,
yi)点或右下方的P2(xi+1, yi-1)点,取舍的方法取决于判别式di,di的定义如下:
di = F(xi+1, yi-0.5) = b2(xi+1)2
+ a2(yi-0.5)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P1为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2
+ a2(yi-0.5)2 – a2b2
= di + b2(2xi + 3)
计算出di的增量是b2(2xi
+ 3)。同理,若di >= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P2为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+1, yi+1-0.5) = b2(xi+2)2
+ a2(yi-1.5)2 – a2b2
= d1 + b2(2xi+3) + a2(-2yi+2)
计算出di的增量是b2(2xi+3)+a2(-2yi+2)。计算di的增量的目的是减少计算量,提高算法效率,每次判断一个点时,不必完整的计算判别式di,只需在上一次计算出的判别式上增加一个增量即可。
接下来继续讨论下部区域椭圆弧的生成,如图(4)所示:

图(4)中点画椭圆算法对下部区域处理示意图
假设当前位置是P(xi, yi),则下一个可能的点就是P点左下方的P1(xi
-1, yi-1)点或下方的P2(xi, yi-1)点,取舍的方法同样取决于判别式di,di的定义如下:
di = F(xi+0.5, yi-1) = b2(xi+0.5)2
+ a2(yi-1)2 – a2b2
若di < 0,表示像素点P1和P2的中点在椭圆内,这时可取P2为下一个像素点。此时xi+1
= xi + 1,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+1.5)2
+ a2(yi-2)2 – a2b2 =
di + b2(2xi+2)+a2(-2yi+3)
计算出di的增量是b2(2xi+2)+a2(-2yi+3)。同理,若di
>= 0,表示像素点P1和P2的中点在椭圆外,这时应当取P1为下一个像素点。此时xi+1
= xi,yi+1 = yi - 1,代入判别式di得到di+1:
di+1 = F(xi+1+0.5, yi+1-1) = b2(xi+0.5)2
+ a2(yi-2)2 – a2b2 =
d1 + a2(-2yi+3)
计算出di的增量是a2(-2yi+3)。
中点画椭圆算法从(0, b)点开始,第一个中点是(1, b – 0.5),判别式d的初始值是:
d0 = F(1, b–0.5) = b2 + a2(-b+0.25)
上部区域生成算法的循环终止条件是:2b2(x + 1) >= 2a2(y – 0.5),下部区域的循环终止条件是y
= 0,至此,中点画椭圆算法就可以完整给出了:
| 20 void MP_Ellipse(int xc , int yc , int a, int b) 21 { 22 double sqa = a * a; 23 double sqb = b * b; 24 25 double d = sqb + sqa * (-b + 0.25); 26 int x = 0; 27 int y = b; 28 EllipsePlot(xc, yc, x, y); 29 while( sqb * (x + 1) < sqa * (y - 0.5)) 30 { 31 if (d < 0) 32 { 33 d += sqb * (2 * x + 3); 34 } 35 else 36 { 37 d += (sqb * (2 * x + 3) + sqa * (-2 * y + 2)); 38 y--; 39 } 40 x++; 41 EllipsePlot(xc, yc, x, y); 42 } 43 d = (b * (x + 0.5)) * 2 + (a * (y - 1)) * 2 - (a * b) * 2; 44 while(y > 0) 45 { 46 if (d < 0) 47 { 48 d += sqb * (2 * x + 2) + sqa * (-2 * y + 3); 49 x++; 50 } 51 else 52 { 53 d += sqa * (-2 * y + 3); 54 } 55 y--; 56 EllipsePlot(xc, yc, x, y); 57 } 58 } |
2、 Bresenham算法
中点画椭圆法中,计算判别式d使用了浮点运算,影响了椭圆的生成效率。如果能将判别式规约到整数运算,则可以简化计算,提高效率。于是人们针对中点画椭圆法进行了多种改进,提出了很多种中点生成椭圆的整数型算法,Bresenham椭圆生成算法就是其中之一。
在生成椭圆上部区域时,以x轴为步进方向,如图(5-a)所示:

图(5)Bresenham椭圆生成算法判别式
x每步进一个单位,就需要在判断y保持不变还是也步进减1,bresenham算法定义判别式为:
D = d1 – d2
如果D < 0,则取P1为下一个点,否则,取P2为下一个点。采用判别式D,避免了中点算法因y-0.5而引入的浮点运算,使得判别式规约为全整数运算,算法效率得到了很大的提升。根据椭圆方程,可以计算出d1和d2分别是:
d1 = a2(yi2 – y2)
d2 = a2(y2 – yi+12)
以(0, b)作为椭圆上部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di + 2b2(2xi
+ 3) (Di < 0)
Di+1 = Di + 2b2(2xi
+ 3) – 4a2(yi - 1) (Di >= 0)
D0 = 2b2 – 2a2b + a2
在生成椭圆下部区域时,以y轴为步进方向,如图(5-b)所示,y每步进减一个单位,就需要在判断x保持不变还是步进加一个单位,对于下部区域,计算出d1和d2分别是:
d1 = b2(xi+12 – x2)
d2 = b2(x2 – xi2)
以(xp, yp)作为椭圆下部区域的起点,将其代入判别式D可以得到如下递推关系:
Di+1 = Di – 4a2(yi
- 1) + 2a2 (Di < 0)
Di+1 = Di + 2b2(xi
+ 1) – 4a2(y - 1) + 2a2 + b2 (Di >= 0)
D0 = b2(xp + 1)2
+b2xp2 - 2a2b2 + 2a2(yp
- 1)2
根据以上分析,Bresenham椭圆生成算法的实现就比较简单了:
| 61 void Bresenham_Ellipse(int xc , int yc , int a, int b) 62 { 63 int sqa = a * a; 64 int sqb = b * b; 65 66 int x = 0; 67 int y = b; 68 int d = 2 * sqb - 2 * b * sqa + sqa; 69 EllipsePlot(xc, yc, x, y); 70 int P_x = ROUND_INT( (double)sqa/sqrt((double)(sqa+sqb)) ); 71 while(x <= P_x) 72 { 73 if(d < 0) 74 { 75 d += 2 * sqb * (2 * x + 3); 76 } 77 else 78 { 79 d += 2 * sqb * (2 * x + 3) - 4 * sqa * (y - 1); 80 y--; 81 } 82 x++; 83 EllipsePlot(xc, yc, x, y); 84 } 85 86 d = sqb * (x * x + x) + sqa * (y * y - y) - sqa * sqb; 87 while(y >= 0) 88 { 89 EllipsePlot(xc, yc, x, y); 90 y--; 91 if(d < 0) 92 { 93 x++; 94 d = d - 2 * sqa * y - sqa + 2 * sqb * x + 2 * sqb; 95 } 96 else 97 { 98 d = d - 2 * sqa * y - sqa; 99 } 100 } 101 } |
参考资料:
【1】计算几何:算法设计与分析周培德
清华大学出版社 2005年
【2】计算几何:算法与应用德贝尔赫(邓俊辉译)
清华大学出版社 2005年
【3】计算机图形学孙家广、杨常贵清华大学出版社 1995年
椭圆的中点生成算法
第二种方法
椭圆中点生成算法
椭圆对称性质原理:
(1)圆是满足x轴对称的,这样只需要计算原来的1/2点的位置;
(2)圆是满足y轴对称的,这样只需要计算原来的1/2点的位置;
通过上面分析可以得到实际上我们计算椭圆生成时候,只需要计算1/4个椭圆就可以实现对于所有点的生成了。
例如:分析出来目标点(x,y)必然存在(x,-y),(-x,y),(-x,-y)的另外3个点。关于中心画圆算法,通过计算x
= 0到 y = 0
的1/4椭圆的范围,然后通过对称原理得到其他3/4个点的信息。(R2表示椭圆厂轴的半径)
椭圆中点生成算法是将椭圆在第一象限中分为两个部分:
(1)对于斜率绝对值小于1的区域内在x方向取单位量;
(2)对于斜率绝对值大于1的区域内在y方向取单位量;
斜率可以通过椭圆的标准方程中获得为
K = - (ry*ry)*x/(rx*rx)*y;
这里中点椭圆生成算法同样和Bresenham算法有很多相似之处,同样有一个决定下一个位置的关键值P来做权衡处理。在中点画椭圆算法中,通过平移的方法将假设圆心在坐标原点,然后计算,最后再平移到真实原心位置。
中点椭圆算法内容:
1,输入椭圆的两个半径r1和r2,并且输入椭圆的圆心。设置初始点(x0,y0)的位置为(0,r2);
2,计算区域1中央决策参数的初始值
p = ry*ry - rx*rx*ry + 1/4*(rx*rx);
3,在区域1中的每个Xn为止,从n
= 0 开始,直到|K|(斜率)小于-1时后结束;
(1)如果p < 0
,绘制下一个点(x+1,y),并且计算
p = p + r2*r2*(3+2*x);
(2)如果P >=0 ,绘制下一个点(x+1,y-1),并且计算
p = p + r2*r2*(3+2*point.x) - 2*r1*r1*(y-1)
4,设置新的参数初始值;
p = ry*ry(X0+1/2)*(X0+1/2) + rx*rx*(Y0-1) - rx*rx*ry*ry;
5,在区域2中的每个Yn为止,从n
= 0开始,直到y = 0时结束。
(1)如果P>0的情况下,下一个目标点为(x,y-1),并且计算
p = p - 2rx*rx*(Yn+1) + rx*rx;
(2)如果p<=0的情况下,下一个目标点为(x+1,y-1),并且计算
p = p - 2rx*rx*Y(n+1) + 2ry*ry*(Xn+1)+rx*rx;
6,更具对称性原理计算其他3个象限的坐标。
7,急速拿出中心位置在(x1,y1)的位置
x = x + x1;
y = y + y1;
实例代码:
#include <iostream>
#include <math.h>
using namespace std;
struct Point{
int x;
int y;
};
void PointsEllipse(int x,int y,int r1,int r2){
Point point;
int p ;//参数
int k ; //斜率
point.x = 0;
point.y = r2;
//
计算区域1中央决策参数的初始值
p =
r2*r2 - r1*r1*r2 + 1/4*(r1*r1);
while( point.x < point.y){
if( p < 0){
point.x ++;
p = p + r2*r2*(3+2*point.x);
}
else{
point.x++;
point.y--;
p = p + r2*r2*(3+2*point.x) - 2*r1*r1*(point.y-1) ;
}
temp.x = point.x + x;
temp.y = point.y + y;
printf("Point X:%d Y:%d\r\n",temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",temp.x,-temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,-temp.y);
}
p = r2*r2*(0+1/2)*(0+1/2) + r1*r1*(r1-1)*(r1-1) - r1*r1*r2*r2;
while(point.y > 0){
if(p > 0){
point.y--;
p = p - 2*r1*r1*point.y - 2*r1*r1 + r1*r1;
}
else{
point.y--;
point.x++;
p = p - 2*r1*r1*point.y - 2*r1*r1 + r1*r1 + 2*r2*r2*point.x + 2*r2*r2 ;
}
temp.x = point.x + x;
temp.y = point.y + y;
printf("Point X:%d Y:%d\r\n",temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",temp.x,-temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,temp.y);
printf("Point X:%d Y:%d\r\n",-temp.x,-temp.y);
}
}
相关文章推荐
- 椭圆生成算法---中点画椭圆法
- 计算机图形学(二)输出图元_6_OpenGL曲线函数_3_椭圆生成算法
- 椭圆的中点生成算法
- 算法系列之十三:椭圆的生成算法 .
- 计算机图形学 – 椭圆的中点生成算法
- 【OpenGL】中点圆、椭圆生成算法
- 椭圆的生成算法
- 算法系列之十三:椭圆的生成算法
- 椭圆的绘画算法――(旋转、填充)
- 计算机图形学—DDA直线生成算法
- n个数全排列的非递归生成算法,C实现
- .NET平台下带权限控制的TreeView控件节点生成算法(转载)
- 一个迷宫生成算法
- vb的GUID生成算法
- 一个排列、组合的生成算法
- NET平台下带权限控制的TreeView控件节点生成算法(转载)
- C++算法系列之日历生成的算法代码
- 在java中实现图形学中的椭圆算法
- .NET平台下带权限控制的TreeView控件节点生成算法 选择自 navy_koo 的 Blog
- .NET平台下带权限控制的TreeView控件节点生成算法
