您的位置：首页 > 其它

【Leetcode】动态规划问题详解（持续更新）

2014-11-24 00:54 896 查看

1、动态规划算法步骤（Dynamic Programming）

动态规划算法一般用来求解最优化问题，当问题有很多可行解，而题目要求寻找这些解当中的“最大值”/“最小值”时，通常可以采用DP。
动态规划算法与分治法相似，都是通过组合子问题的解来求解原问题。所不同的是，动态规划应用于子问题重叠的情况，在递归求解子问题的时候，一些子子问题可能是相同的，这种情况下，分治法会反复地计算同样的子问题，而动态规划对于相同的子问题只计算一次。

动态规划算法的设计步骤：
1、刻画最优解的结构特征（寻找最优子结构）
2、递归地定义最优解的值（确定递归公式，动态规划法的重点就是这个）
3、计算最优解的值（有两种方法：带备忘录自顶向下法、自底向上法）
4、利用计算出的信息构造一个最优解（通常是将具体的最优解输出）

2、leetcode上适合用DP求解的问题

题目	OJ地址	目录
Triangle	https://oj.leetcode.com/problems/triangle/	3.1
Maximum Subarray	https://oj.leetcode.com/problems/maximum-subarray/	3.2
Palindrome Partitioning II	https://oj.leetcode.com/problems/palindrome-partitioning-ii/	3.3
Minimum Path Sum	https://oj.leetcode.com/problems/minimum-path-sum/	3.4
Maximal Rectangle	https://oj.leetcode.com/problems/maximal-rectangle/	3.5
Interleaving String	https://oj.leetcode.com/problems/interleaving-string/	3.6
Edit Distance	https://oj.leetcode.com/problems/edit-distance/	3.7
Decode Ways	https://oj.leetcode.com/problems/decode-ways/	3.8
Best Time to Buy and Sell Stoc I&II&III	https://oj.leetcode.com/problems/best-time-to-buy-and-sell-stock/	3.9
Scramble String	https://oj.leetcode.com/problems/scramble-string/	3.10
Distinct Subsequences	https://oj.leetcode.com/problems/distinct-subsequences/	3.11
Word Break I&II	https://oj.leetcode.com/problems/word-break/	3.12
Unique Paths I & II	https://oj.leetcode.com/problems/unique-paths/	3.4

3、leetcode相关题目

3.1 Triangle

3.1.1 题目

Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.

For example, given the following triangle

[
     [2],
    [3,4],
   [6,5,7],
  [4,1,8,3]
]

The minimum path sum from top to bottom is

(i.e., 2 + 3 + 5 + 1 =
11).

Note:

Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.

3.1.2 分析

题目大意：从最顶端往下走，寻找和最小的路径。
显然，从最顶端往下走有很多条路径可以走，但是每一条路径的sum不一样，题目要求sum最小，属于最优化问题，考虑动态规划。

如果用暴力破解，复杂度如何？观察题目所给的三角形，对于每个“节点”，往下都有两条路可以走，比如2可以往3、4走，3可以往6、5走，4可以往5、7走.......类似于二叉树，如果有n行，则一共有路径2^n条，时间复杂度O(2^n)。

用动态规划的话，时间复杂度可以降到O(n^2)。下面按照动态规划的步骤来分析这道题：
#1 最优解的结构特征
第一个步骤要搞清楚怎么将问题分解为更小的子问题。上面已经提到，“2”往下走都有两条路可以选择，分别是“3”、“4”，因此从2出发的最优路径，其实就是从“3”出发的最优路径、从“4”出发的最优路径这两者中sum最小的一条。

#2 确定递归求解公式
用f(i,j)表示从点(i,j)出发的最优路径的sum，根据上面分析，易得递归公式：f(i,j)=min{f(i+1,j),f(i+1,j+1)}+Val(i,j)
Val(i,j)表示点(i,j)的值。

#3 根据递归公式求解
分别用“自底向上”、“带备忘录的自顶向下”两种方法，见3.1.3代码

3.1.3 参考代码

自底向上法，注意到f(0,0)取决于f(1,0)、f(1,1); f(1,0)又取决于f(2,0)、f(2,1)......所以从最底层开始计算是比较自然的做法，而最底层的最短路径和就是节点本身的值，因此实际上是从倒数第二层开始计算。

<span style="font-size:18px;">int minimumTotal(vector<vector<int> > &triangle) {
        int row=triangle.size();    //行,第row行的元素有row个
        vector<vector<int> > f(triangle);
        //用f[m]
记录从triangle[m]
出发到叶子节点的最短路径和。也可以直接用triangle代替f，但会改变triangle
        
        for(int x=row-2;x>=0;x--)
           for(int y=0;y<=x;y++)
              f[x][y]=min(f[x+1][y],f[x+1][y+1])+triangle[x][y];
        return f[0][0];
    }</span>

(自底向上法的程序是迭代形式的)

带备忘录的自顶向下法

<span style="font-size:18px;">class Solution {
public:
    int minimumTotal(vector<vector<int> > &triangle) {
        int row=triangle.size();    //行
        vector<vector<int> > f(triangle);   //f[m]
表示从triangle[m]
出发到叶子节点的最短路径和
        for(int m=0;m<row-1;m++)
           for(int n=0;n<=m;n++)
              f[m]
=INT_MAX;         //与自底向上的方法不同，备忘录法必须将其初始化为标识值，以便“查找备忘录”
	f[row-1]=triangle[row-1];       //最后一行保持原值
        return dp(0,0,triangle,f);      //从根出发
    }
private:
   int dp(int x,int y,vector<vector<int> > &triangle,vector<vector<int> > &f){
        if(f[x][y]!=INT_MAX) return f[x][y];   //查找备忘录，如果已经计算过，直接返回，避免重复计算
        f[x][y]=min(dp(x+1,y,triangle,f),dp(x+1,y+1,triangle,f))+triangle[x][y];
        return f[x][y];
   }
};</span>

（备忘录法的代码是递归形式的，但不同于递归程序的是，它有备忘录f[m]
，不会重复计算相同子问题）

3.2 Maximum Subarray

3.2.1 题目

Find the contiguous subarray within an array (containing at least one number) which has the largest sum.

For example, given the array

[−2,1,−3,4,−1,2,1,−5,4]

,

the contiguous subarray

[4,−1,2,1]

has the largest sum =

3.2.2 分析

题目大意：给定一个数组，求最大连续子段和。
经典问题来的，搜索一下，解法多种多样：
暴力枚举法，时间复杂度O(n^3)。以数组的每个元素为子段起点，并以该起点后面的每一个元素为子段终点，计算该子段和，不断更新最大子段。

分治法，时间复杂度O(nlogn)。将数组等分为a[0..n/2]、a[n/2+1..n]，则a[0...n]的最大子段存在的位置有三种情况，第一种是只在数组a[0..n/2]里，第二种是只在a[n/2+1..n]里，第三种是横跨a[0..n/2]和a[n/2+1..n]，对于第三种，只需要从a[n/2]开始分别往两边搜索出和最大的子段，拼接起来即题目所求的最大子段。

动态规划法，时间复杂度O(n)。
从头到尾遍历数组，对于每个元素，它可以加入之前保存的subarray，也可以以它为起点另起一个subarray。什么情况加入什么情况另起？当之前的subarray大于0时，我们认为subarray对后续是有利的，将当前元素加入subarray，反之若subarray小于0，则另起一个subarray。在这个过程中，subarray的值一直在变，但有可能变大，也有可能变小，所以要不断地更新sum=max{sum,subarray}。

#确定递归公式
b[j]=max{a[i]++a[j]},1<=i<=j,且1<=j<=n,则所求的最大子段和为max b[j]，1<=j<=n。
由b[j]的定义可知，当b[j-1]>0时b[j]=b[j-1]+a[j]，否则b[j]=a[j]。
因此递归公式为：b[j]=max(b[j-1]+a[j],a[j])，1<=j<=n。
根据递归公式可以写出如下代码

3.2.3 代码

<span style="font-size:18px;">int maxSubArray(int A[], int n) {
        int sum=INT_MIN,b=0;     
        for(int i=0;i<n;i++)
        {
            b=max(A[i],b+A[i]);
            sum=max(sum,b);
        }
        return sum;
    }</span>

3.3 Palindrome Partitioning II

3.3.1 题目

Given a string s, partition s such that every substring of the partition is a palindrome.

Return the minimum cuts needed for a palindrome partitioning of s.

For example, given s =

"aab"

,

Return

since the palindrome partitioning

["aa","b"]

could
be produced using 1 cut.

3.3.2 分析

题目大意：给定一个字符串，返回最小的切割数，使得切割后形成的所有字符串都是回文的。

我们知道，对于一个长度为n的字符串，它里面可以切割的位置有n-1个，每个位置可切割可不切割，这样一共会产生2^(n-1)种方案，我们的任务就是从所有方案中，找出满足以下两个条件的那个方案：1、切割后形成的所有字符串都是回文的。2、符合条件1的所有方案中切割数最小。

如果用暴力破解，复杂度是O(2^n)。我们模拟一下这个过程，比如s="abcde"，从a后面切割，然后递归求解“bcde”的最小切割数；从b后面切割，然后递归求解“cde”的最小切割数....可以发现求解 “bcde”最小切割数这个子问题包含了求解“cde”最小切割数这个字问题，也就是说有重叠子问题，而暴力破解法重复计算了这些子问题。
显然，应该用动态规划：
#1
首先，我们用p[i][j]=true表示字符串s[i...j]是回文字符串，false表示非回文串。这里p[i][j]作为备忘录，是为了避免重复地判断p[i][j]是否为回文串。
易知，当s[i]==s[j]并且s[i+1..j-1]为回文串时，s[i..j]为回文串。或者当s[i..j]长度小于3时，s[i]==s[j]则s[i..j]是回文串
因此可以得到：p[i][j]= s[i]==s[j] && (j-i<2 || p[i+1][j-1])

#2
用f[i]表示字符串s[i...n-1]的最小切割数，则可以得到递归公式：f[i]=min{ f[ j+1]+1 }，其中i<=j<=n
根据这个递归公式，我们想得到f[i]，就必须先得到f[i+1]、f[i+2].....f[n-1]，因此计算f[]的顺序是从f[n-1]往前倒f[0]，f[0]即我们想要的。
下面用例子模拟一遍：
s=“abcdddd”，长度为7，f[i]初始化最坏情况下的切割数,即s[i...n-1]每一处都切割，那么：
初始时f[0]=6,f[1]=5,f[2]=4,.....f[6]=0，然后：

（1）计算f[6]，即s[6..6]的最小切割数，显然是0，然后计算出f[5]、f[4]、f[3]也同样是0

（2）计算f[2],即“cdddd”的最小切割数

判断p[2][2]即"c"是否回文，若是，更新f[2]，这里显然是，故 f[2]=min{f[2],1+f[3]}=min{4,1}=1;

接着判断p[2][3]即"cd"是否回文，若是,f[2]=min{f[2],1+f[4]},这里因为"cd"不是回文，所以不更新f[2]

p[2][4]、p[2][5]、p[2][6]都不是，不更新f[2]，最后f[2]=1

（3）计算f[1]，即"bcdddd”的最小切割数

判断p[1][1]即"b"是否回文，显然是，f[1]=min{f[1],1+f[2]}=min{5,2}=2;

判断p[1][2]即"bc"是否回文，不是回文，不更新f[1]

p[1][3]、p[1][4]、p[1][5]、p[1][6]都不是，不更新f[1]，最后f[1]=2

（4）计算f[0],即"abcdddd”的最小切割数

判断p[0][0]即"a"是否回文，显然是，f[0]=min{f[0],1+f[1]}=min{6,3}=3;

p[0][1]、p[0][2]、p[0][3]、p[0][4]、p[0][5]、p[0][6]都不是，不更新f[0]，最后f[0]=3

3.3.3 代码

<span style="font-size:18px;">int minCut(string s) {
      int n=s.size();
      int f[n+1];       //f[i]表示字符串s[i...n-1]的最小切割数
      for(int i=0;i<=n;i++)    
         f[i]=n-i-1;   //初始化为最坏情况,即每一处都切割。注意f
=-1是故意多出来的一个
      
      bool p

;    
      memset(p,false,n*n);
      /*确定p[i][j]*/
      for(int i=n-1;i>=0;i--)   
        for(int j=i;j<n;j++){  
            p[i][j]= s[i]==s[j] && (j-i<2 || p[i+1][j-1]);   
        }//当s[i]==s[j]并且s[i+1..j-1]为回文串时，s[i..j]才为回文串。当s[i..j]长度小于3则只需判断s[i]==s[j]
        
     /*计算f[]*/
      for(int i=n-1;i>=0;i--)    
         for(int j=i;j<n;j++){
             if(p[i][j]) f[i]=min(f[i],1+f[j+1]);
         } //这段代码其实可以直接将if语句写到上面的for for循环里，这里只是为了思想清晰 
         
      return f[0];
    }</span>

3.4 Unique Paths、Unique Paths II、Minimum Path Sum

3.4.1 Unique Paths

3.4.1.1 题目

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

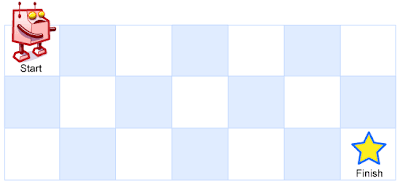
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

3.4.1.2 分析

题目大意：给定一个m*n的网格，限定每次只能向右或向下走，问从start到finish一共有多少条路径。

这道题很容易想到分治法，记start下边相邻的格子为startbelow，start右边相邻的格子为startright，则start到finish的路径数可以表示为：uniquePaths(start)=uniquePaths(startbelow)+uniquePaths(startright)。
分治法的代码很简单，但是复杂度太高，超时：

int uniquePaths(int m, int n) {
        if(m<1 || n<1) return 0;
        if(m==1 && n==1) return 1;
        return uniquePaths(m-1,n)+uniquePaths(m,n-1);
    }

很明显，分治法对于重叠的子问题进行了重复计算，比如startbelow向右、startright向下会到达同一个格子g，上面的递归程序会计算两次uniquePaths(g)。

动态规划的特点之一就是避免重复计算重叠子问题，为了避免重复计算，我们应该建一个备忘录p[i][j]，记录一个i * j的网格的path个数。比如对于start，它到finish的路径数为p[3][7]。
现在，我们想要得到p[3][7]，就得首先得到p[2][7]和p[3][6]，同样p[2][7]又取决于p[1][7]和p[2][6]......
所以递归公式为：p[i][j]=p[i-1][j]+p[i][j-1]。

自然地，我们可以采用动态规划的自底向上法，先计算p[1][1]，然后p[1][2]、p[1][3].....

当然，也可以采用自顶向下法，代码见3.4.1.3

3.4.1.3 代码

自底向上法代码，时间复杂度O(n^2)

int uniquePaths(int m, int n) {
        if(m<1 || n<1) return 0;
        if(m==1 && n==1) return 1;
        int p[m+1][n+1];//p[i][j]表示：一个iXj的grid的path个数。p[m]
即为所求

        for(int i=1;i<=m;i++)
           for(int j=1;j<=n;j++){  
               if(i==1 || j==1) p[i][j]=1; //对于只有一行或者一列的网格，路径数肯定为1
               else p[i][j]=p[i-1][j]+p[i][j-1];
           }
        return p[m]
;        
    }

自顶向下法

class Solution {
public:
    int uniquePaths(int m, int n) {
       this->p=vector<vector<int>> (m+1,vector<int>(n+1,0));
       return dfs(m,n);
    }
private:
   vector<vector<int>> p;
   int dfs(int m,int n){
       if(m<1 || n<1) return 0;
       if(m==1 && n==1) return 1;
       return getp(m-1,n)+getp(m,n-1);
   }
   int getp(int m,int n ){
       if(p[m]
!=0) return p[m]
;
       else p[m]
=dfs(m,n);
   }
};

3.4.2 Unique Paths II

3.4.2.1 题目

Follow up for "Unique Paths":

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as

and

respectively
in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[
  [0,0,0],
  [0,1,0],
  [0,0,0]
]

The total number of unique paths is

.

Note: m and n will be at most 100.

3.4.2.2 分析

题目大意：这道题跟上一道只有一点不同，给定的网格中一些格子是设有障碍的。

只要在上一道的基础上稍加修改就行：对于那些有障碍的（即值为1）的格子（i，j），其p[i][j]=0，因为不可能从它开始找到任何一条路径到达终点。
另外，对于只有一列或者一行的网格，比如[0 0 0 1 0 0]，起点到终点的路径数p[1][6]为0，因为只能向右走，而且中间碰到障碍。
除了以上这些处理，递归式仍然是：p[i][j]=p[i-1][j]+p[i][j-1]。
据此写出以下代码，采用自顶向上，注意p[i][j]表示的网格i*j是从原网格中以“终点”为右下顶点截取下来的，比如对于题目所给的3*3网格，p[2][2]表示的网格是: 1 0
0 0

3.4.2.3 代码

int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid) {
        if(obstacleGrid.empty()) return 0;
        int m=obstacleGrid.size();
        int n=obstacleGrid[0].size();
        int p[m+1][n+1];//p[i][j]表示：iXj的grid的path个数（该grid是从obstacleGrid中以“终点”为右下顶点截取下来的）

        for(int i=1;i<=m;i++)
           for(int j=1;j<=n;j++){  
               if(obstacleGrid[m-i][n-j]==1) p[i][j]=0;   //有障碍，p[i][j]=0
               else if(i==1 && j==1){     //p[1][1]单独处理
                  p[i][j]=1;
               }
               else if(i==1){
                    p[1][j]=p[1][j-1];   //只能向右，取决于p[1][j-1]
               }
               else if(j==1){            
                   p[i][1]=p[i-1][1];    //只能向下，取决于p[i-1][1]
               }
               else  p[i][j]=p[i-1][j]+p[i][j-1];    //能向下或向右
           }
        return p[m]
;
    }

3.4.3 Minimum Path Sum

3.4.3.1 题目

Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.

Note: You can only move either down or right at any point in time.

3.4.3.2 分析

题目大意：给定一个m*n的网格，每个格子里面有非负数，找出从top-left（同3.4.1题图中的start）到bottom-right（同3.4.1题图中的finish）的具有最小sum的路径。

仍然可以用上两题的思路，只不过p[i][j]存储的不是i*j网格的路径数，而是i*j网格的最小sum。
递归公式：p[i][j]=val[i,j]+min{ p[i-1][j]，p[i][j-1] } val[i,j]表示格子(i,j)的值。
当然，对于只有一行的网格p[1][j]=val[i,j]+p[1][j-1]，对于只有一列的网格，p[i][1]=val[i,j]+p[i-1][1]

3.4.3.3 代码

int minPathSum(vector<vector<int> > &grid) {
        if(grid.empty()) return 0;
        int m=grid.size();
        int n=grid[0].size();
        int p[m+1][n+1];      //p[i][j]表示iXj的grid的最小PathSum（该grid是从grid中以“终点”为右下顶点截取下来的），p[m]
即为所求
        /*自底向上法*/
        for(int i=1;i<=m;i++)
           for(int j=1;j<=n;j++){       
               if(i==1 && j==1)  p[1][1]=grid[m-1][n-1];              //p[1][1]单独处理
               else if(i==1)   p[i][j]=grid[m-i][n-j]+p[i][j-1];      //i=1，只能向右走
               else if(j==1)   p[i][j]=grid[m-i][n-j]+p[i-1][j];      //j=1，只能向下走
               else p[i][j]=grid[m-i][n-j]+min(p[i-1][j],p[i][j-1]);  //能向下或向右
           }
        return p[m]
;
    }

内容来自用户分享和网络整理，不保证内容的准确性，如有侵权内容，可联系管理员处理

标签：

相关文章推荐

新的分享

章节导航