线性代数(五十二) : 对角化与惯性律
2014-04-08 20:31
351 查看
本节介绍将二次型转化为对角矩阵.
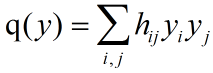
进行变换:
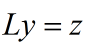
使得q在新变量z下的矩阵表示是对角矩阵.即:
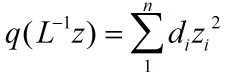
假设q的矩阵表示中对角线的元素不全为0.假设h11不为零.将全体包含y1的项归类:
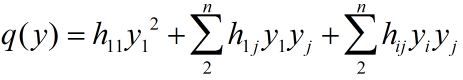
由于H是对称矩阵.因此q可以写为:
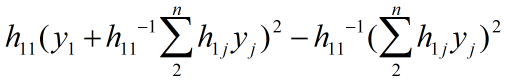
令:
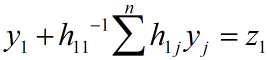
则:
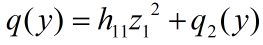
其中:
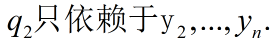
如果q的矩阵表示中对角线的元素都为零.但非对角线元素不全为零.不妨设:
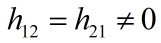
则可以引入新变量:
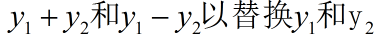
在新变量的矩阵表示中对角线元素不全为零.
如果q的矩阵表示中全体元素都为零.则:
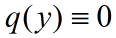
定理无需证明.
对变量个数n进行归纳.由(13)式可知,如果含n-1个变量的二次型q2能化为(11)式的形式.
则q也能.由(12)式可知:如果y2,...,yn左乘以某个可逆矩阵等于z2,...,zn,则必存在可逆矩阵使得全体y左乘以该矩阵等于全体z.
这一性质常备称为惯性律.
为了证明该定理需要一条引理:
S是R^n的子空间.称q在S上正定,如果:
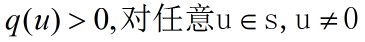
类似的定义负定:
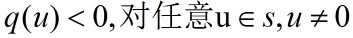
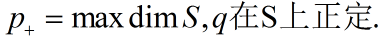
类似的有:
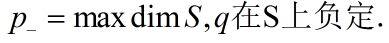
引理二的证明省略.
引理二表明P+和P-由二次型q本身确定.与(11)式中的变量的选取无关.由于:

因此证明了惯性律.
1 对角化
对于二次型: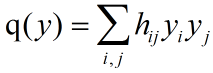
进行变换:
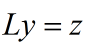
使得q在新变量z下的矩阵表示是对角矩阵.即:
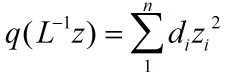
假设q的矩阵表示中对角线的元素不全为0.假设h11不为零.将全体包含y1的项归类:
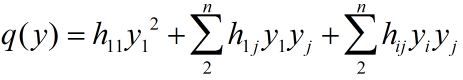
由于H是对称矩阵.因此q可以写为:
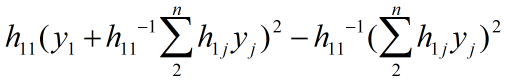
令:
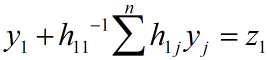
则:
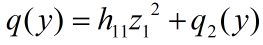
其中:
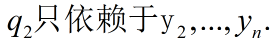
如果q的矩阵表示中对角线的元素都为零.但非对角线元素不全为零.不妨设:
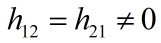
则可以引入新变量:
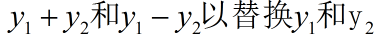
在新变量的矩阵表示中对角线元素不全为零.
如果q的矩阵表示中全体元素都为零.则:
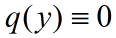
定理无需证明.
对变量个数n进行归纳.由(13)式可知,如果含n-1个变量的二次型q2能化为(11)式的形式.
则q也能.由(12)式可知:如果y2,...,yn左乘以某个可逆矩阵等于z2,...,zn,则必存在可逆矩阵使得全体y左乘以该矩阵等于全体z.
2 惯性律
对于上边引入新变量对角化q的方式通常不止一种.但无论哪种方式.上式中对角线元素di为正负和零的数目都不变.这一性质常备称为惯性律.
为了证明该定理需要一条引理:
3 正定与负定
以P+,P-,P0 分别表示(11)式中的正负项和零的数目.S是R^n的子空间.称q在S上正定,如果:
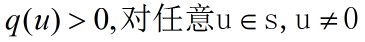
类似的定义负定:
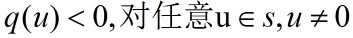
4 引理
R^n的使q正定的最大子空间的维数是P+: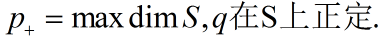
类似的有:
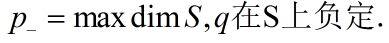
引理二的证明省略.
引理二表明P+和P-由二次型q本身确定.与(11)式中的变量的选取无关.由于:

因此证明了惯性律.
相关文章推荐
- 我对特征值与特征向量的理解
- 马尔科夫状态转移矩阵的一个性质,以及一个直观的图形证明
- 线性代数(一)(Linear Algobra with Application)steven J.Leon(Eighth Edition)
- 线性代数(二)(Linear Algobra with Application)steven J.Leon(Eighth Edition)
- 行列式求值
- poj 1222 (高斯消元)
- 高斯消元模板
- poj 1681 Painter's Problem
- poj 3185 The Water Bowls
- FZU 1704 Turn off the light
- 线性代数(一) : 线性空间
- 线性代数(二) : 矩阵与矩阵运算
- 线性代数(三) : 线性映射与矩阵
- 线性代数(四) :矩阵乘法的性质与分块矩阵的运算
- 线性代数(五) :子空间及向量张成的空间
- 线性代数(六) : 线性相关与线性无关
- 线性代数(七) : 子空间的基与维数
- 线性代数(八) : 消元法和矩阵的初等变换
- 线性代数(九) : 矩阵的行简化阶梯型和标准型
- 线性代数(十) : 矩阵的列空间与零空间
