圆锥:转为平面几何 UVA 1473 Dome of Circus
2014-02-10 23:34
281 查看
A travelling circus faces a tough challenge in designing the dome for its performances. The circus has a number of shows that happen above the stage in the air under the dome. Various rigs, supports, and anchors must be installed over the stage, but under
the dome. The dome itself must rise above the center of the stage and has a conical shape. The space under the dome must be air-conditioned, so the goal is to design the dome that contains minimal volume.
You are given a set of n points in the space;
(xi, yi, zi) for
1
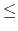
i
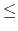
n
are the coordinates of the points in the air above the stage that must be covered by the dome. The ground is denoted by the plane
z = 0, with positive z coordinates going up. The center of the stage is on the ground at the point (0, 0, 0).
The tip of the dome must be located at some point with coordinates
(0, 0, h) with h > 0. The dome must have a conical shape that touches the ground at the circle with the center in the point (0, 0, 0) and with the radius of
r. The dome must contain or touch all the
n given points. The dome must have the minimal volume, given the above constraints.
Input
The input file contains several test cases, each of them as described below.
The first line of the input file contains a single integer number
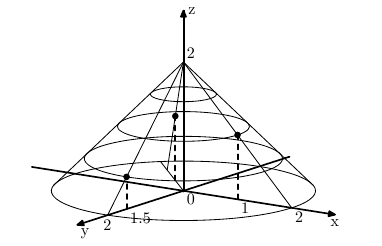
n (1
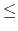
n
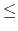
10000)
-- the number of points under the dome. The following n lines describe points with three floating point numbers
xi, yi, and
zi per line -- the coordinates of
i-th point. All coordinates do not exceed 1000 by their absolute value and have at most 2 digits after decimal point. All
zi are positive. There is at least one point with non-zero
xi or yi.
Output
For each test case, write to the output file a single line with two floating point numbers
h and r -- the height and the base radius of the dome. The numbers must be precise up to 3 digits after decimal point.
Sample Input
Sample Output
题意:在三维坐标系中给出一些点,你需要画出一个圆锥,把所有的点都包含在里面,点能在锥面上,并且使得这个圆锥的体积最小。问底面半径和高是多少。
思路:我们可以把三维的降为二维的,因为圆锥非常的对称,我们把所有的点都画在平面直角坐标系的第一象限就行了,x坐标为sqrt(x*x+y*y),y坐标为z。然后我们的问题其实相当于是在第一象限有一些点,然后我们要画一条直线使得所有点在这条直线的下方,并且原来图形的体积最小。我们通过斜截式可以得出体积的表达式,对其求导我们能知道当k = -2y/x 时,体积最小。
不难发现这条直线一定会穿过至少一个点,因为如果直线上面没有点话,我们能将线下移直到与某个相交,而这个过程会使体积变小。那要怎么样才能把所有的点都包括在直线下面呢?我们先把所有的点从左到右进行排序,对于x相同的我们只保留y最大的,因为直线显然不会与y较小的相交,如果与y较小的相交,那个y较大的就不能在直线的“下方”了。排好序和去“重”后,我们按照从左到右的顺序一个点一个点开始连线,目的是算出每个点的斜率的取值范围,连线的过程中我们要保证斜率单调递减,即越来越倾斜。如果某条直线的斜率比上一条大的话,那么我们不能把这个点与上一个点相连,删掉上一个点,看能不能与再上一个点相连,如果还是不是递减,继续删,知道是递减为止,至于为什么?你画画图能直观的看出来,我就不说了,这个过程有点像构造凸包吧。这样下来后,我们就能得到每个点的斜率范围了。然后看这个范围内有能不能取理论上的最小值,否则的话,就取边界值。这样下来,求h,r的过程的复杂度是O(n)
(每个点最多进一次栈和出一次栈),总的时间复杂度是O(nlogn) 排序的时间。这道题就得到比较圆满的解决了。
代码:
#include<iostream>
#include<cstdio>
#include<string.h>
#include<math.h>
#include<cstring>
#include<algorithm>
using namespace std;
#define eps 1e-9
struct Point
{
Point (double xx=0,double yy=0) : x(xx) , y(yy) { }
double x;
double y;
};
typedef Point Vector;
Vector operator+(Vector v1,Vector v2) { return Vector(v1.x+v2.x,v1.y+v2.y); }
Vector operator-(Vector v1,Vector v2) { return Vector(v1.x-v2.x,v1.y-v2.y); }
Vector operator*(Vector v, double p) { return Vector(v.x*p,v.y*p); }
Vector operator/(Vector v,double p) { return Vector(v.x/p,v.y/p); }
bool operator < (Point a,Point b) { return a.x < b.x || (a.x==b.x && a.y > b.y); }
int dcmp(double x)
{
if (fabs(x) < eps) return 0;
return x < 0 ? -1 : 1;
}
bool operator==(const Point & a,const Point & b)
{
return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}
double Dot(Vector A,Vector B) { return A.x*B.x+A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A,A)); }
double Angle(Vector A,Vector B) { return acos(Dot(A,B)/Length(A)/Length(B)); }
double Cross(Vector A,Vector B) { return A.x*B.y-A.y*B.x; }
double Area2(Point a,Point b,Point c) { return Cross(b-a,c-a); }
Vector Rotate(Vector A,double rad)
{
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
Vector Normal(Vector A) { double L = Length(A); return Vector(-A.y/L,A.x/L); }
//点和直线
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)
{
Vector u = P-Q;
double t = Cross(w,u) / Cross(v,w);
return P+v*t;
}
double DistanceToLine(Point P,Point A,Point B)
{
Vector v1 = B-A , v2 = P-A;
return fabs(Cross(v1,v2))/Length(v1);
}
double DistanceToSegment(Point P,Point A,Point B)
{
if (A==B) return Length(P-A);
Vector v1 = B-A , v2 = P-A , v3 = P-B;
if (dcmp(Dot(v1,v2)) < 0) return Length(v2);
else if (dcmp(Dot(v1,v3)) > 0) return Length(v3);
else return fabs(Cross(v1,v2))/Length(v1);
}
Point GetLineProjection(Point P,Point A,Point B)
{
Vector v = B-A;
return A+v*(Dot(v,P-A)/Dot(v,v));
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
double c1 = Cross(a2-a1,b1-a1) , c2 = Cross(a2-a1,b2-a1) ,
c3 = Cross(b2-b1,a1-b1) , c4 = Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4)<0;
}
bool OnSegment(Point p,Point a,Point b) {
return dcmp(Cross(a-p,b-p))==0 && dcmp(Dot(a-p,b-p)) < 0;
}
//--------------------------------------------------------------------------------------------
const int maxn = 10000+10;
const double inf = 1e15;
const double PI = 4*atan(1.0);
Point p[maxn];
double pre[maxn];
int S[maxn] , c;
int n;
inline double K(Point a,Point b) { return (a.y-b.y)/(a.x-b.x); }
void input()
{
for (int i = 0 ; i < n ; ++i) {
double x , y , z;
scanf("%lf%lf%lf",&x,&y,&z);
p[i] = Point(sqrt(x*x+y*y),z);
}
sort(p,p+n);
int m = 0;
for (int i = 0 ; i < n ; ++i)
if (dcmp(p[m].x-p[i].x)!=0) p[++m] = p[i];
n = m+1;
}
void solve()
{
c = 0;
S[c++] = 0; pre[0] = 0;
for (int i = 1 ; i < n ; ++i) {
while (c > 0) {
double k = K(p[i],p[S[c-1]]);
if (dcmp(k-pre[c-1]) <= 0) { pre[c] = k; break; }
--c;
}
S[c++] = i;
}
pre[c] = -inf;
double ans = inf , h , r;
for (int i = 0 ; i < c ; ++i ) {
double maxk = pre[i];
double mink = pre[i+1];
double hh , rr;
if (dcmp(maxk)<0) {
hh = maxk*(-p[S[i]].x)+p[S[i]].y;
rr = -p[S[i]].y/maxk+p[S[i]].x;
if (dcmp(ans-rr*rr*hh*PI) > 0) {
h = hh;
r = rr;
ans = rr*rr*hh*PI;
}
}
double k = -2*p[S[i]].y/p[S[i]].x;
if (dcmp(mink-k)<=0 && dcmp(k-maxk)<=0) {
hh = k*(-p[S[i]].x)+p[S[i]].y;
rr = -p[S[i]].y/k+p[S[i]].x;
double area = PI*rr*rr*hh;
if (dcmp(area-ans)<0) {
h = hh , r = rr;
ans = area;
}
}
}
printf("%.3lf %.3lf\n",h,r);
}
int main()
{
while (scanf("%d",&n)==1)
{
input();
solve();
}
}
the dome. The dome itself must rise above the center of the stage and has a conical shape. The space under the dome must be air-conditioned, so the goal is to design the dome that contains minimal volume.
You are given a set of n points in the space;
(xi, yi, zi) for
1
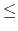
i
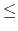
n
are the coordinates of the points in the air above the stage that must be covered by the dome. The ground is denoted by the plane
z = 0, with positive z coordinates going up. The center of the stage is on the ground at the point (0, 0, 0).
The tip of the dome must be located at some point with coordinates
(0, 0, h) with h > 0. The dome must have a conical shape that touches the ground at the circle with the center in the point (0, 0, 0) and with the radius of
r. The dome must contain or touch all the
n given points. The dome must have the minimal volume, given the above constraints.

Input
The input file contains several test cases, each of them as described below.The first line of the input file contains a single integer number
n (1
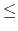
n
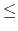
10000)
-- the number of points under the dome. The following n lines describe points with three floating point numbers
xi, yi, and
zi per line -- the coordinates of
i-th point. All coordinates do not exceed 1000 by their absolute value and have at most 2 digits after decimal point. All
zi are positive. There is at least one point with non-zero
xi or yi.
Output
For each test case, write to the output file a single line with two floating point numbersh and r -- the height and the base radius of the dome. The numbers must be precise up to 3 digits after decimal point.
Sample Input
1 1.00 0.00 1.00 2 1.00 0.00 1.00 0.00 1.50 0.50 3 1.00 0.00 1.00 0.00 1.50 0.50 -0.50 -0.50 1.00
Sample Output
3.000 1.500 2.000 2.000 2.000 2.000
题意:在三维坐标系中给出一些点,你需要画出一个圆锥,把所有的点都包含在里面,点能在锥面上,并且使得这个圆锥的体积最小。问底面半径和高是多少。
思路:我们可以把三维的降为二维的,因为圆锥非常的对称,我们把所有的点都画在平面直角坐标系的第一象限就行了,x坐标为sqrt(x*x+y*y),y坐标为z。然后我们的问题其实相当于是在第一象限有一些点,然后我们要画一条直线使得所有点在这条直线的下方,并且原来图形的体积最小。我们通过斜截式可以得出体积的表达式,对其求导我们能知道当k = -2y/x 时,体积最小。
不难发现这条直线一定会穿过至少一个点,因为如果直线上面没有点话,我们能将线下移直到与某个相交,而这个过程会使体积变小。那要怎么样才能把所有的点都包括在直线下面呢?我们先把所有的点从左到右进行排序,对于x相同的我们只保留y最大的,因为直线显然不会与y较小的相交,如果与y较小的相交,那个y较大的就不能在直线的“下方”了。排好序和去“重”后,我们按照从左到右的顺序一个点一个点开始连线,目的是算出每个点的斜率的取值范围,连线的过程中我们要保证斜率单调递减,即越来越倾斜。如果某条直线的斜率比上一条大的话,那么我们不能把这个点与上一个点相连,删掉上一个点,看能不能与再上一个点相连,如果还是不是递减,继续删,知道是递减为止,至于为什么?你画画图能直观的看出来,我就不说了,这个过程有点像构造凸包吧。这样下来后,我们就能得到每个点的斜率范围了。然后看这个范围内有能不能取理论上的最小值,否则的话,就取边界值。这样下来,求h,r的过程的复杂度是O(n)
(每个点最多进一次栈和出一次栈),总的时间复杂度是O(nlogn) 排序的时间。这道题就得到比较圆满的解决了。
代码:
#include<iostream>
#include<cstdio>
#include<string.h>
#include<math.h>
#include<cstring>
#include<algorithm>
using namespace std;
#define eps 1e-9
struct Point
{
Point (double xx=0,double yy=0) : x(xx) , y(yy) { }
double x;
double y;
};
typedef Point Vector;
Vector operator+(Vector v1,Vector v2) { return Vector(v1.x+v2.x,v1.y+v2.y); }
Vector operator-(Vector v1,Vector v2) { return Vector(v1.x-v2.x,v1.y-v2.y); }
Vector operator*(Vector v, double p) { return Vector(v.x*p,v.y*p); }
Vector operator/(Vector v,double p) { return Vector(v.x/p,v.y/p); }
bool operator < (Point a,Point b) { return a.x < b.x || (a.x==b.x && a.y > b.y); }
int dcmp(double x)
{
if (fabs(x) < eps) return 0;
return x < 0 ? -1 : 1;
}
bool operator==(const Point & a,const Point & b)
{
return dcmp(a.x-b.x)==0 && dcmp(a.y-b.y)==0;
}
double Dot(Vector A,Vector B) { return A.x*B.x+A.y*B.y; }
double Length(Vector A) { return sqrt(Dot(A,A)); }
double Angle(Vector A,Vector B) { return acos(Dot(A,B)/Length(A)/Length(B)); }
double Cross(Vector A,Vector B) { return A.x*B.y-A.y*B.x; }
double Area2(Point a,Point b,Point c) { return Cross(b-a,c-a); }
Vector Rotate(Vector A,double rad)
{
return Vector(A.x*cos(rad)-A.y*sin(rad),A.x*sin(rad)+A.y*cos(rad));
}
Vector Normal(Vector A) { double L = Length(A); return Vector(-A.y/L,A.x/L); }
//点和直线
Point GetLineIntersection(Point P,Vector v,Point Q,Vector w)
{
Vector u = P-Q;
double t = Cross(w,u) / Cross(v,w);
return P+v*t;
}
double DistanceToLine(Point P,Point A,Point B)
{
Vector v1 = B-A , v2 = P-A;
return fabs(Cross(v1,v2))/Length(v1);
}
double DistanceToSegment(Point P,Point A,Point B)
{
if (A==B) return Length(P-A);
Vector v1 = B-A , v2 = P-A , v3 = P-B;
if (dcmp(Dot(v1,v2)) < 0) return Length(v2);
else if (dcmp(Dot(v1,v3)) > 0) return Length(v3);
else return fabs(Cross(v1,v2))/Length(v1);
}
Point GetLineProjection(Point P,Point A,Point B)
{
Vector v = B-A;
return A+v*(Dot(v,P-A)/Dot(v,v));
}
bool SegmentProperIntersection(Point a1,Point a2,Point b1,Point b2)
{
double c1 = Cross(a2-a1,b1-a1) , c2 = Cross(a2-a1,b2-a1) ,
c3 = Cross(b2-b1,a1-b1) , c4 = Cross(b2-b1,a2-b1);
return dcmp(c1)*dcmp(c2) < 0 && dcmp(c3)*dcmp(c4)<0;
}
bool OnSegment(Point p,Point a,Point b) {
return dcmp(Cross(a-p,b-p))==0 && dcmp(Dot(a-p,b-p)) < 0;
}
//--------------------------------------------------------------------------------------------
const int maxn = 10000+10;
const double inf = 1e15;
const double PI = 4*atan(1.0);
Point p[maxn];
double pre[maxn];
int S[maxn] , c;
int n;
inline double K(Point a,Point b) { return (a.y-b.y)/(a.x-b.x); }
void input()
{
for (int i = 0 ; i < n ; ++i) {
double x , y , z;
scanf("%lf%lf%lf",&x,&y,&z);
p[i] = Point(sqrt(x*x+y*y),z);
}
sort(p,p+n);
int m = 0;
for (int i = 0 ; i < n ; ++i)
if (dcmp(p[m].x-p[i].x)!=0) p[++m] = p[i];
n = m+1;
}
void solve()
{
c = 0;
S[c++] = 0; pre[0] = 0;
for (int i = 1 ; i < n ; ++i) {
while (c > 0) {
double k = K(p[i],p[S[c-1]]);
if (dcmp(k-pre[c-1]) <= 0) { pre[c] = k; break; }
--c;
}
S[c++] = i;
}
pre[c] = -inf;
double ans = inf , h , r;
for (int i = 0 ; i < c ; ++i ) {
double maxk = pre[i];
double mink = pre[i+1];
double hh , rr;
if (dcmp(maxk)<0) {
hh = maxk*(-p[S[i]].x)+p[S[i]].y;
rr = -p[S[i]].y/maxk+p[S[i]].x;
if (dcmp(ans-rr*rr*hh*PI) > 0) {
h = hh;
r = rr;
ans = rr*rr*hh*PI;
}
}
double k = -2*p[S[i]].y/p[S[i]].x;
if (dcmp(mink-k)<=0 && dcmp(k-maxk)<=0) {
hh = k*(-p[S[i]].x)+p[S[i]].y;
rr = -p[S[i]].y/k+p[S[i]].x;
double area = PI*rr*rr*hh;
if (dcmp(area-ans)<0) {
h = hh , r = rr;
ans = area;
}
}
}
printf("%.3lf %.3lf\n",h,r);
}
int main()
{
while (scanf("%d",&n)==1)
{
input();
solve();
}
}
相关文章推荐
- UVA 1473 - Dome of Circus(三分+计算几何)
- UVa 1473 - Dome of Circus 三分
- uva 1473 - Dome of Circus (几何 + 二分)
- Dome of Circus - UVa 1473 几何 凸包
- UVa 1473 Dome of Circus(求凸包)
- UVA1473 - Dome of Circus
- UVALive 4986 Dome of Circus(三分、凸包、凸性函数)
- G - Dome of Circus UVALive - 4986 (三分)
- UVA 1473&LA 4986 - Dome of Circus
- uva 1473 - Dome of Circus
- hdu 3756 || Dome of Circus || 2010 Northeastern European Regional Contest(三分)
- HDOJ_ACM_Dome of Circus
- HDU 3756 Dome of Circus 三分
- hdoj 3756 Dome of Circus(三分)
- 【三分】HDU3756 Dome of Circus
- UVA-10938 - Flea circus(dfs)
- UVALive - 3902 Network 无根树转为有跟树+搜索+贪心
- UVALive - 3902 Network 无根树转为有跟树
- ACM--steps--4.1.7--Dome of Circus(三分)
- hdu 3756 Dome of Circus(模拟退火)
