Recursive implementation of the Gaussian filter
2013-08-21 16:47
295 查看
摘要
这篇论文,我们提出来高斯滤波的递归实现方法。这个实现产生了一个无限脉冲响应滤波器(infinite impulse response filter),它每个维度有六个MADDs(multiplications and additions)独立于高斯核的sigma值。与Deriche 实现相比,递归滤波器的系数值更容易根据要求的Gaussian sigma值计算。通常来说,该算法比 直接用二维高斯模板卷积,分解2次一维高斯卷积和频域高斯滤波的实现速度更快。
1.介绍
由于以数字图像为基础的人类视觉模型的研究,边缘检测、尺度空间的研究,以及模拟量的精确测量技术的发展,使得高斯滤波在图像滤波领域一直承担着中心角色。
通常一维或多维的高斯滤波是通过高斯模板的卷积实现的。作为一个简单滤波器的重复卷积或是作为一个需要复杂过程来计算滤波系数的逼近高斯模板的递归滤波。(as repeated convolutions with a simpler filter sucn as a uniform filter, or as a recursive filtering with an approximation to the Gaussian that
requires a complicated procedure to determine the filter coefficients) 重复卷积方法要求的(appeals to)中心极限定理表明,在这个限制下,重复的脉冲响应卷积,如一个简单的均匀滤波器,能导致与高斯滤波器等效的卷积结果。
高斯模板离散卷积的每一维由下式给出:
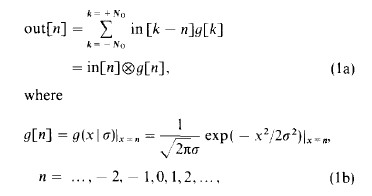
sigma 是实数,N0是个整数。通常N0选择为5倍的sigma取整。在给定的值N0下,连续高斯函数g(x)在g(x=0)处的值下降了因数3.7*10(-6)。
基于“平方”核的重复卷积给出了每一维度的实现如下:
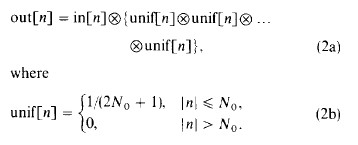
通常使用三次均值滤波器卷积来逼近高斯滤波。对于要求的sigma,要求N0等于sigma取整。只有有限数量的高斯滤波器可以用这种方法创建,因为我们不得不使用整数N0的值。
通过Deriche研发的技术是一个复杂的设计步骤为每个选择的sigma(The technique developed by Deriche involves a complicated design step for every choice of sigma。由于这个原因,Deriche发展了一个可供选择的non-Gaussian递归滤波,每个维度的脉冲响应如下h
=k(a|n|+1)exp(-a|n|)。这个滤波确实有些好的性质,但是也有一些缺点(
it is non-isotropic(in 2-D not circularly symmetric) and it is not the target filter, the Gaussian )。
多维高斯滤波的可分离性(that is,exp(-(n2+m2))=exp(-n2)exp(-m2),使得检测每个算法单个维度的计算复杂度是合适的。对每个维度直接卷积需要使用(2N0+1)MADDs(multiplications and additions)。得益于高斯滤波的对称性,计算复杂度可以减少到2N0次加法,N0+1次乘法。重复卷积的花费是2N0次加法。Deriche 逼近高斯法需要12MADDs每个维度,他的迭代递归滤波器需要8MADDs每维。
论文在递归结构基础上提出了一个高斯滤波的迭代实现。该算法产生了一个无限脉冲响应滤波器(infinite impulse response filter),它每个维度有六个MADDs(multiplications and additions)独立于高斯核的sigma值。通常该算法比上面提到的算法都要快,而且不失准确性。
2.Laplace域规范
我们的方法基于对高斯函数的合理的逼近:
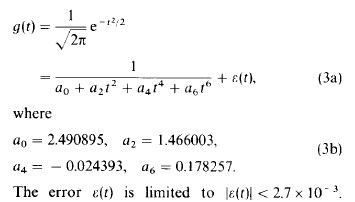
相对于g(t)在t=0时取得的最大值,误差的最大值为|eps(t)|/g(0) < 0.68%。论文【1】中还给出了高斯函数的一个更复杂的逼近,但涉及到十次多项式,为了说明问题,我们用上面的逼近就足够了。
我们并不把这个逼近直接作为对高斯脉冲响应的逼近,而是作为高斯函数傅里叶变换的逼近。也就是说,G(w)=F{g(x|sigma)},我们有著名的结论:
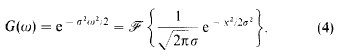
由于接着会变得明显的原因,我们用q代替sigma来给出合理的逼近:
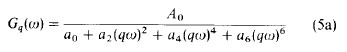
with s = jw,等价的laplace变换如下:
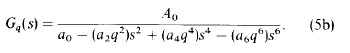
式(5b)可以分解为两项的乘积,Gq(s)=Gl(s)Gr(s) Gl(s)极点在左半平面,Gr(s)极点在右半平面
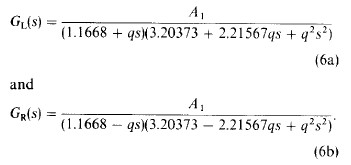
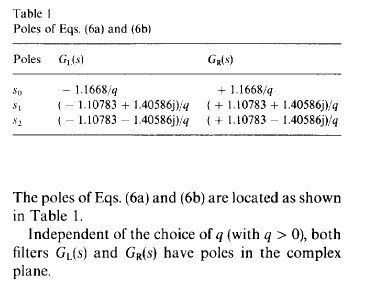
3. Z域的表示
式(6a)表示一个因果、稳定的微分方程,可以被转变为一个因果、稳定的差分方程,从Gl(s)转换到Hl(z)。式(6b)表示一个非因果、稳定的微分方程,可以被转变为一个非因果、稳定的差分方程,从Gr(s)转换到Hr(z)。微分转差分的标准技术是用双线性转换 s=(1-z(-1))/(1+z(-1))。然而这个技术会导致零值传递函数Hl(z)和Hr(z),这方面的影响是我们想要避免的。此外,双线性转换还有一些其他的缺点,参见附录A。
代替双线性转换,我们选择后向差分技术用 (y
-y[n-1]) / T 来逼近导数 dy/dt ,这样我们用s = (1-z(-1)) / T 来替换 s。像双线性转换一样,这种方法也具有把因果、稳定的Gl(s) 映射到因果、稳定的 Hl(z)的性质。而且,没有零值被引入到Hl(z)与Hr(z)中。为生成Hr(z)我们使用后向差分方程 (y
-y[n-1]) / T 来逼近导数 dy/dt ,s 用 s = (z-1)/T替换。同样,这种方法也具有把非因果、稳定的Gr(s)
映射到因果、稳定的 Hr(z)的性质。设T=1,我们可以得到:
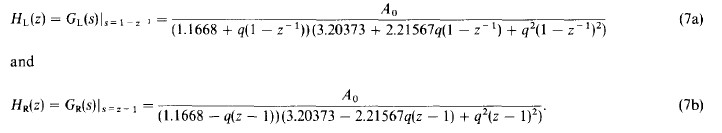
两式可以写成z(-1) , z 的标准多项式形式,分别如下:

这种实现启发我们使用如下的滤波策略。输入数据先用对应式(8a)的差分方程进行正向滤波,我们把这个输出结果记做w
,然后用对应式(8b)的差分方程进行反向滤波。差分方程如下:
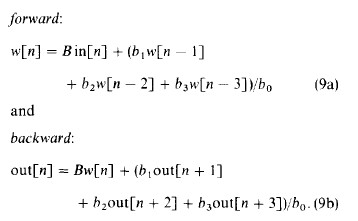
两个滤波器有相同的归一化常数B,B可以用滤波器传递函数应该为1.0对于频率w=W=0这个约束来指定。得到下式:
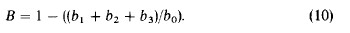
例子。现在让我们来看一个使用这个步骤的例子。我们开始选取 q=5.0。使用式(8c)得到b1/b0 = 2.36565, b2/b0 = -1.89709, b3/b0 = 0.51601, B = 0.01543. 这个高斯滤波的递归实现脉冲响应连同一个sigma=6.09的高斯连续曲线一起显示在Fig.1(a) 。为了增强显示高斯函数的细节在图Fig.(1b)中显示了放大了的效果。
对这个例子的一些观察值是很有用的。式(6a),(6b)和相关的极点(list in Table 1) 表明,每个分开项(forward and backward)的脉冲响应会产生振荡。然而,我们观察到的高斯递归滤波器的脉冲响应h
并没有这些反应。
递归高斯滤波的脉冲响应标准差并不是式(4),(5a),(5b)建议的q的值。上例中用到的q=5.0,而最小均方差拟合高斯脉冲响应得到的sigma=6.09。在-33*sigma到33*sigma间测量,对于q=5.0的均方根误差为rms=2.8*10(-4),最大绝对误差为|eps|=1.7*10(-3),根平方误差为rs=5.6*10(-3)。我们下面讨论这个问题。
4. 选择q
这篇论文,我们提出来高斯滤波的递归实现方法。这个实现产生了一个无限脉冲响应滤波器(infinite impulse response filter),它每个维度有六个MADDs(multiplications and additions)独立于高斯核的sigma值。与Deriche 实现相比,递归滤波器的系数值更容易根据要求的Gaussian sigma值计算。通常来说,该算法比 直接用二维高斯模板卷积,分解2次一维高斯卷积和频域高斯滤波的实现速度更快。
1.介绍
由于以数字图像为基础的人类视觉模型的研究,边缘检测、尺度空间的研究,以及模拟量的精确测量技术的发展,使得高斯滤波在图像滤波领域一直承担着中心角色。
通常一维或多维的高斯滤波是通过高斯模板的卷积实现的。作为一个简单滤波器的重复卷积或是作为一个需要复杂过程来计算滤波系数的逼近高斯模板的递归滤波。(as repeated convolutions with a simpler filter sucn as a uniform filter, or as a recursive filtering with an approximation to the Gaussian that
requires a complicated procedure to determine the filter coefficients) 重复卷积方法要求的(appeals to)中心极限定理表明,在这个限制下,重复的脉冲响应卷积,如一个简单的均匀滤波器,能导致与高斯滤波器等效的卷积结果。
高斯模板离散卷积的每一维由下式给出:
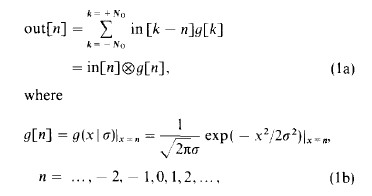
sigma 是实数,N0是个整数。通常N0选择为5倍的sigma取整。在给定的值N0下,连续高斯函数g(x)在g(x=0)处的值下降了因数3.7*10(-6)。
基于“平方”核的重复卷积给出了每一维度的实现如下:
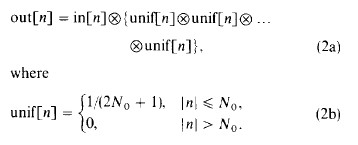
通常使用三次均值滤波器卷积来逼近高斯滤波。对于要求的sigma,要求N0等于sigma取整。只有有限数量的高斯滤波器可以用这种方法创建,因为我们不得不使用整数N0的值。
通过Deriche研发的技术是一个复杂的设计步骤为每个选择的sigma(The technique developed by Deriche involves a complicated design step for every choice of sigma。由于这个原因,Deriche发展了一个可供选择的non-Gaussian递归滤波,每个维度的脉冲响应如下h
=k(a|n|+1)exp(-a|n|)。这个滤波确实有些好的性质,但是也有一些缺点(
it is non-isotropic(in 2-D not circularly symmetric) and it is not the target filter, the Gaussian )。
多维高斯滤波的可分离性(that is,exp(-(n2+m2))=exp(-n2)exp(-m2),使得检测每个算法单个维度的计算复杂度是合适的。对每个维度直接卷积需要使用(2N0+1)MADDs(multiplications and additions)。得益于高斯滤波的对称性,计算复杂度可以减少到2N0次加法,N0+1次乘法。重复卷积的花费是2N0次加法。Deriche 逼近高斯法需要12MADDs每个维度,他的迭代递归滤波器需要8MADDs每维。
论文在递归结构基础上提出了一个高斯滤波的迭代实现。该算法产生了一个无限脉冲响应滤波器(infinite impulse response filter),它每个维度有六个MADDs(multiplications and additions)独立于高斯核的sigma值。通常该算法比上面提到的算法都要快,而且不失准确性。
2.Laplace域规范
我们的方法基于对高斯函数的合理的逼近:
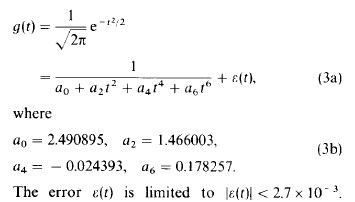
相对于g(t)在t=0时取得的最大值,误差的最大值为|eps(t)|/g(0) < 0.68%。论文【1】中还给出了高斯函数的一个更复杂的逼近,但涉及到十次多项式,为了说明问题,我们用上面的逼近就足够了。
我们并不把这个逼近直接作为对高斯脉冲响应的逼近,而是作为高斯函数傅里叶变换的逼近。也就是说,G(w)=F{g(x|sigma)},我们有著名的结论:
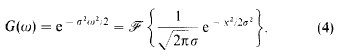
由于接着会变得明显的原因,我们用q代替sigma来给出合理的逼近:
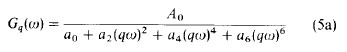
with s = jw,等价的laplace变换如下:
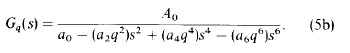
式(5b)可以分解为两项的乘积,Gq(s)=Gl(s)Gr(s) Gl(s)极点在左半平面,Gr(s)极点在右半平面
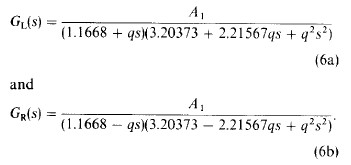

3. Z域的表示
式(6a)表示一个因果、稳定的微分方程,可以被转变为一个因果、稳定的差分方程,从Gl(s)转换到Hl(z)。式(6b)表示一个非因果、稳定的微分方程,可以被转变为一个非因果、稳定的差分方程,从Gr(s)转换到Hr(z)。微分转差分的标准技术是用双线性转换 s=(1-z(-1))/(1+z(-1))。然而这个技术会导致零值传递函数Hl(z)和Hr(z),这方面的影响是我们想要避免的。此外,双线性转换还有一些其他的缺点,参见附录A。
代替双线性转换,我们选择后向差分技术用 (y
-y[n-1]) / T 来逼近导数 dy/dt ,这样我们用s = (1-z(-1)) / T 来替换 s。像双线性转换一样,这种方法也具有把因果、稳定的Gl(s) 映射到因果、稳定的 Hl(z)的性质。而且,没有零值被引入到Hl(z)与Hr(z)中。为生成Hr(z)我们使用后向差分方程 (y
-y[n-1]) / T 来逼近导数 dy/dt ,s 用 s = (z-1)/T替换。同样,这种方法也具有把非因果、稳定的Gr(s)
映射到因果、稳定的 Hr(z)的性质。设T=1,我们可以得到:
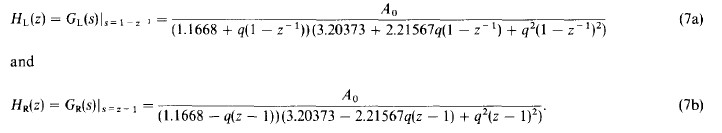
两式可以写成z(-1) , z 的标准多项式形式,分别如下:

这种实现启发我们使用如下的滤波策略。输入数据先用对应式(8a)的差分方程进行正向滤波,我们把这个输出结果记做w
,然后用对应式(8b)的差分方程进行反向滤波。差分方程如下:
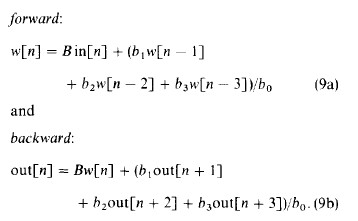
两个滤波器有相同的归一化常数B,B可以用滤波器传递函数应该为1.0对于频率w=W=0这个约束来指定。得到下式:
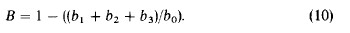
例子。现在让我们来看一个使用这个步骤的例子。我们开始选取 q=5.0。使用式(8c)得到b1/b0 = 2.36565, b2/b0 = -1.89709, b3/b0 = 0.51601, B = 0.01543. 这个高斯滤波的递归实现脉冲响应连同一个sigma=6.09的高斯连续曲线一起显示在Fig.1(a) 。为了增强显示高斯函数的细节在图Fig.(1b)中显示了放大了的效果。
对这个例子的一些观察值是很有用的。式(6a),(6b)和相关的极点(list in Table 1) 表明,每个分开项(forward and backward)的脉冲响应会产生振荡。然而,我们观察到的高斯递归滤波器的脉冲响应h
并没有这些反应。
递归高斯滤波的脉冲响应标准差并不是式(4),(5a),(5b)建议的q的值。上例中用到的q=5.0,而最小均方差拟合高斯脉冲响应得到的sigma=6.09。在-33*sigma到33*sigma间测量,对于q=5.0的均方根误差为rms=2.8*10(-4),最大绝对误差为|eps|=1.7*10(-3),根平方误差为rs=5.6*10(-3)。我们下面讨论这个问题。
4. 选择q
相关文章推荐
- Recursive implementation of the Gaussian filter[翻译]
- Implementation of Gaussian filter
- VC ++中添加了一个新类后cannot find the definition (implementation) of this function
- A Fast Approximation of the Bilateral Filter using a Signal Processing Approach
- Simple implementation of the BinaryTree preorder traversal, inorder traversal, post traversal
- This implementation is not part of the Windows Platform FIPS validated ...
- cannot find the definition (implementation) of this function 解决方法
- Cannot find the definition(implementation) of this function
- The MS implementation of float window
- The Implementation of RFCOMM in Android
- Algorithm: The implementation of Trie Tree (C++)
- The Backend Implementation of HugeGraph
- A filter or servlet of the current chain does not support asynchronous operations
- Notes on the implementation of encryption in Android 3.0
- Cannot find the definition (implementation) of this function
- WPF Compilation Error: Unknown Error. This implementation is not part of the Windows Platform FIPS validated cryptographic algor
- About the Implementation of .Net Framework's HashTable
- The Design and Implementation of Two-dimensional Vector Graphics Interactive Tools Based on “Smart Handle”
- 16 Which statement most accurately describes the implementation of a SQL Access Advisor recommendati
- Algorithm: The implementation of Trie Tree (C++)
