SVM算法实现(一)
2012-12-04 14:31
197 查看
转载地址:http://blog.csdn.net/techq/article/details/6171688
关键字(keywords):SVM 支持向量机 SMO算法 实现 机器学习
如果对SVM原理不是很懂的,可以先看一下入门的视频,对帮助理解很有用的,然后再深入一点可以看看这几篇入门文章,作者写得挺详细,看完以后SVM的基础就了解得差不多了,再然后买本《支持向量机导论》作者是Nello
Cristianini 和 John Shawe-Taylor,电子工业出版社的。然后把书本后面的那个SMO算法实现就基本上弄懂了SVM是怎么一回事,最后再编写一个SVM库出来,比如说像libsvm等工具使用,呵呵,差不多就这样。这些是我学习SVM的整个过程,也算是经验吧。
下面是SVM的简化版SMO算法,我将结合Java代码来解释一下整个SVM的学习训练过程,即所谓的train训练过程。那么什么是SMO算法呢?
SMO算法的目的无非是找出一个函数f(x),这个函数能让我们把输入的数据x进行分类。既然是分类肯定需要一个评判的标准,比如分出来有两种情况A和B,那么怎么样才能说x是属于A类的,或不是B类的呢?就是需要有个边界,就好像两个国家一样有边界,如果边界越明显,则就越容易区分,因此,我们的目标是最大化边界的宽度,使得非常容易的区分是A类还是B类。
在SVM中,要最大化边界则需要最小化这个数值:
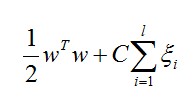
w:是参量,值越大边界越明显
C代表惩罚系数,即如果某个x是属于某一类,但是它偏离了该类,跑到边界上后者其他类的地方去了,C越大表明越不想放弃这个点,边界就会缩小
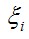
代表:松散变量
但问题似乎还不好解,又因为SVM是一个凸二次规划问题,凸二次规划问题有最优解,于是问题转换成下列形式(KKT条件):
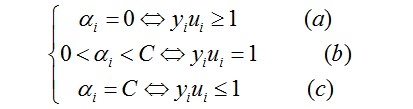
…………(1)
这里的ai是拉格朗日乘子(问题通过拉格朗日乘法数来求解)
对于(a)的情况,表明ai是正常分类,在边界内部(我们知道正确分类的点yi*f(xi)>=0)
对于(b)的情况,表明了ai是支持向量,在边界上
对于(c)的情况,表明了ai是在两条边界之间
而最优解需要满足KKT条件,即满足(a)(b)(c)条件都满足
以下几种情况出现将会出现不满足:
yiui<=1但是ai<C则是不满足的,而原本ai=C
yiui>=1但是ai>0则是不满足的而原本ai=0
yiui=1但是ai=0或者ai=C则表明不满足的,而原本应该是0<ai<C
所以要找出不满足KKT的这些ai,并更新这些ai,但这些ai又受到另外一个约束,即
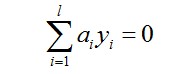
因此,我们通过另一个方法,即同时更新ai和aj,满足以下等式
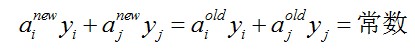
就能保证和为0的约束。
利用yiai+yjaj=常数,消去ai,可得到一个关于单变量aj的一个凸二次规划问题,不考虑其约束0<=aj<=C,可以得其解为:

………………………………………(2)
这里
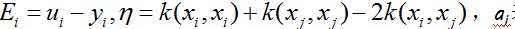
………………(3)
表示旧值,然后考虑约束0<=aj<=C可得到a的解析解为:

…………(4)
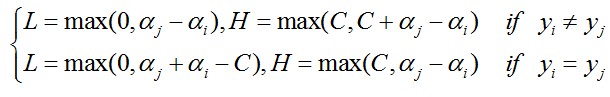
对于
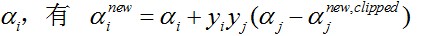
那么如何求得ai和aj呢?
对于ai,即第一个乘子,可以通过刚刚说的那几种不满足KKT的条件来找,第二个乘子aj可以找满足条件

…………………………………………………………………………(5)
b的更新:

在满足条件:
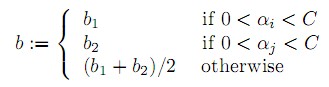
下更新b。……………(6)
最后更新所有ai,y和b,这样模型就出来了,然后通过函数:

……………………………………………………(7)
输入是x,是一个数组,组中每一个值表示一个特征。
输出是A类还是B类。(正类还是负类)
以下是主要的代码段:
[java] view plaincopyprint?
/*
* 默认输入参数值
* C: regularization parameter
* tol: numerical tolerance
* max passes
*/
double C = 1; //对不在界内的惩罚因子
double tol = 0.01;//容忍极限值
int maxPasses = 5; //表示没有改变拉格朗日乘子的最多迭代次数
/*
* 初始化a[], b, passes
*/
double a[] = new double[x.length];//拉格朗日乘子
this.a = a;
//将乘子初始化为0
for (int i = 0; i < x.length; i++) {
a[i] = 0;
}
int passes = 0;
while (passes < maxPasses) {
//表示改变乘子的次数(基本上是成对改变的)
int num_changed_alphas = 0;
for (int i = 0; i < x.length; i++) {
//表示特定阶段由a和b所决定的输出与真实yi的误差
//参照公式(7)
double Ei = getE(i);
/*
* 把违背KKT条件的ai作为第一个
* 满足KKT条件的情况是:
* yi*f(i) >= 1 and alpha == 0 (正确分类)
* yi*f(i) == 1 and 0<alpha < C (在边界上的支持向量)
* yi*f(i) <= 1 and alpha == C (在边界之间)
*
*
*
* ri = y[i] * Ei = y[i] * f(i) - y[i]^2 >= 0
* 如果ri < 0并且alpha < C 则违反了KKT条件
* 因为原本ri < 0 应该对应的是alpha = C
* 同理,ri > 0并且alpha > 0则违反了KKT条件
* 因为原本ri > 0对应的应该是alpha =0
*/
if ((y[i] * Ei < -tol && a[i] < C) ||
(y[i] * Ei > tol && a[i] > 0))
{
/*
* ui*yi=1边界上的点 0 < a[i] < C
* 找MAX|E1 - E2|
*/
int j;
/*
* boundAlpha表示x点处于边界上所对应的
* 拉格朗日乘子a的集合
*/
if (this.boundAlpha.size() > 0) {
//参照公式(5)
j = findMax(Ei, this.boundAlpha);
} else
//如果边界上没有,就随便选一个j != i的aj
j = RandomSelect(i);
double Ej = getE(j);
//保存当前的ai和aj
double oldAi = a[i];
double oldAj = a[j];
/*
* 计算乘子的范围U, V
* 参考公式(4)
*/
double L, H;
if (y[i] != y[j]) {
L = Math.max(0, a[j] - a[i]);
H = Math.min(C, C - a[i] + a[j]);
} else {
L = Math.max(0, a[i] + a[j] - C);
H = Math.min(0, a[i] + a[j]);
}
/*
* 如果eta等于0或者大于0 则表明a最优值应该在L或者U上
*/
double eta = 2 * k(i, j) - k(i, i) - k(j, j);//公式(3)
if (eta >= 0)
continue;
a[j] = a[j] - y[j] * (Ei - Ej)/ eta;//公式(2)
if (0 < a[j] && a[j] < C)
this.boundAlpha.add(j);
if (a[j] < L)
a[j] = L;
else if (a[j] > H)
a[j] = H;
if (Math.abs(a[j] - oldAj) < 1e-5)
continue;
a[i] = a[i] + y[i] * y[j] * (oldAj - a[j]);
if (0 < a[i] && a[i] < C)
this.boundAlpha.add(i);
/*
* 计算b1, b2
* 参照公式(6)
*/
double b1 = b - Ei - y[i] * (a[i] - oldAi) * k(i, i) - y[j] * (a[j] - oldAj) * k(i, j);
double b2 = b - Ej - y[i] * (a[i] - oldAi) * k(i, j) - y[j] * (a[j] - oldAj) * k(j, j);
if (0 < a[i] && a[i] < C)
b = b1;
else if (0 < a[j] && a[j] < C)
b = b2;
else
b = (b1 + b2) / 2;
num_changed_alphas = num_changed_alphas + 1;
}
}
if (num_changed_alphas == 0) {
passes++;
} else
passes = 0;
}
return new SVMModel(a, y, b);
/* * 默认输入参数值 * C: regularization parameter * tol: numerical tolerance * max passes */ double C = 1; //对不在界内的惩罚因子 double tol = 0.01;//容忍极限值 int maxPasses = 5; //表示没有改变拉格朗日乘子的最多迭代次数 /* * 初始化a[], b, passes */ double a[] = new double[x.length];//拉格朗日乘子 this.a = a; //将乘子初始化为0 for (int i = 0; i < x.length; i++) { a[i] = 0; } int passes = 0; while (passes < maxPasses) { //表示改变乘子的次数(基本上是成对改变的) int num_changed_alphas = 0; for (int i = 0; i < x.length; i++) { //表示特定阶段由a和b所决定的输出与真实yi的误差 //参照公式(7) double Ei = getE(i); /* * 把违背KKT条件的ai作为第一个 * 满足KKT条件的情况是: * yi*f(i) >= 1 and alpha == 0 (正确分类) * yi*f(i) == 1 and 0<alpha < C (在边界上的支持向量) * yi*f(i) <= 1 and alpha == C (在边界之间) * * * * ri = y[i] * Ei = y[i] * f(i) - y[i]^2 >= 0 * 如果ri < 0并且alpha < C 则违反了KKT条件 * 因为原本ri < 0 应该对应的是alpha = C * 同理,ri > 0并且alpha > 0则违反了KKT条件 * 因为原本ri > 0对应的应该是alpha =0 */ if ((y[i] * Ei < -tol && a[i] < C) || (y[i] * Ei > tol && a[i] > 0)) { /* * ui*yi=1边界上的点 0 < a[i] < C * 找MAX|E1 - E2| */ int j; /* * boundAlpha表示x点处于边界上所对应的 * 拉格朗日乘子a的集合 */ if (this.boundAlpha.size() > 0) { //参照公式(5) j = findMax(Ei, this.boundAlpha); } else //如果边界上没有,就随便选一个j != i的aj j = RandomSelect(i); double Ej = getE(j); //保存当前的ai和aj double oldAi = a[i]; double oldAj = a[j]; /* * 计算乘子的范围U, V * 参考公式(4) */ double L, H; if (y[i] != y[j]) { L = Math.max(0, a[j] - a[i]); H = Math.min(C, C - a[i] + a[j]); } else { L = Math.max(0, a[i] + a[j] - C); H = Math.min(0, a[i] + a[j]); } /* * 如果eta等于0或者大于0 则表明a最优值应该在L或者U上 */ double eta = 2 * k(i, j) - k(i, i) - k(j, j);//公式(3) if (eta >= 0) continue; a[j] = a[j] - y[j] * (Ei - Ej)/ eta;//公式(2) if (0 < a[j] && a[j] < C) this.boundAlpha.add(j); if (a[j] < L) a[j] = L; else if (a[j] > H) a[j] = H; if (Math.abs(a[j] - oldAj) < 1e-5) continue; a[i] = a[i] + y[i] * y[j] * (oldAj - a[j]); if (0 < a[i] && a[i] < C) this.boundAlpha.add(i); /* * 计算b1, b2 * 参照公式(6) */ double b1 = b - Ei - y[i] * (a[i] - oldAi) * k(i, i) - y[j] * (a[j] - oldAj) * k(i, j); double b2 = b - Ej - y[i] * (a[i] - oldAi) * k(i, j) - y[j] * (a[j] - oldAj) * k(j, j); if (0 < a[i] && a[i] < C) b = b1; else if (0 < a[j] && a[j] < C) b = b2; else b = (b1 + b2) / 2; num_changed_alphas = num_changed_alphas + 1; } } if (num_changed_alphas == 0) { passes++; } else passes = 0; } return new SVMModel(a, y, b);
运行后的结果还算可以吧,测试数据主要是用了libsvm的heart_scale的数据。
预测的正确率达到73%以上。
如果我把核函数从线性的改为基于RBF将会更好点。
最后,说到SVM算法实现包,应该有很多,包括svm light,libsvm,有matlab本身自带的svm工具包等。
另外,完整的代码,我将上传到CSDN下载地址上提供下载。
点击这里下载。
如理解有误敬请指正!谢谢!
我的邮箱:chen-hongqin@163.com
我的其他博客:
百度:http://hi.baidu.com/futrueboy/home
javaeye:http://futrueboy.javaeye.com/
CSDN: http://blog.csdn.net/techq
关键字(keywords):SVM 支持向量机 SMO算法 实现 机器学习
如果对SVM原理不是很懂的,可以先看一下入门的视频,对帮助理解很有用的,然后再深入一点可以看看这几篇入门文章,作者写得挺详细,看完以后SVM的基础就了解得差不多了,再然后买本《支持向量机导论》作者是Nello
Cristianini 和 John Shawe-Taylor,电子工业出版社的。然后把书本后面的那个SMO算法实现就基本上弄懂了SVM是怎么一回事,最后再编写一个SVM库出来,比如说像libsvm等工具使用,呵呵,差不多就这样。这些是我学习SVM的整个过程,也算是经验吧。
下面是SVM的简化版SMO算法,我将结合Java代码来解释一下整个SVM的学习训练过程,即所谓的train训练过程。那么什么是SMO算法呢?
SMO算法的目的无非是找出一个函数f(x),这个函数能让我们把输入的数据x进行分类。既然是分类肯定需要一个评判的标准,比如分出来有两种情况A和B,那么怎么样才能说x是属于A类的,或不是B类的呢?就是需要有个边界,就好像两个国家一样有边界,如果边界越明显,则就越容易区分,因此,我们的目标是最大化边界的宽度,使得非常容易的区分是A类还是B类。
在SVM中,要最大化边界则需要最小化这个数值:
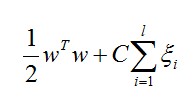
w:是参量,值越大边界越明显
C代表惩罚系数,即如果某个x是属于某一类,但是它偏离了该类,跑到边界上后者其他类的地方去了,C越大表明越不想放弃这个点,边界就会缩小
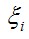
代表:松散变量
但问题似乎还不好解,又因为SVM是一个凸二次规划问题,凸二次规划问题有最优解,于是问题转换成下列形式(KKT条件):
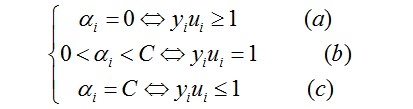
…………(1)
这里的ai是拉格朗日乘子(问题通过拉格朗日乘法数来求解)
对于(a)的情况,表明ai是正常分类,在边界内部(我们知道正确分类的点yi*f(xi)>=0)
对于(b)的情况,表明了ai是支持向量,在边界上
对于(c)的情况,表明了ai是在两条边界之间
而最优解需要满足KKT条件,即满足(a)(b)(c)条件都满足
以下几种情况出现将会出现不满足:
yiui<=1但是ai<C则是不满足的,而原本ai=C
yiui>=1但是ai>0则是不满足的而原本ai=0
yiui=1但是ai=0或者ai=C则表明不满足的,而原本应该是0<ai<C
所以要找出不满足KKT的这些ai,并更新这些ai,但这些ai又受到另外一个约束,即
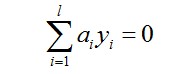
因此,我们通过另一个方法,即同时更新ai和aj,满足以下等式
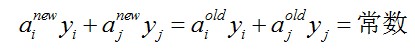
就能保证和为0的约束。
利用yiai+yjaj=常数,消去ai,可得到一个关于单变量aj的一个凸二次规划问题,不考虑其约束0<=aj<=C,可以得其解为:

………………………………………(2)
这里
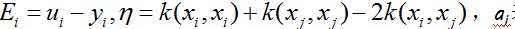
………………(3)
表示旧值,然后考虑约束0<=aj<=C可得到a的解析解为:

…………(4)
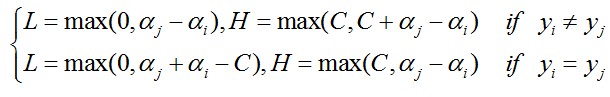
对于
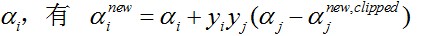
那么如何求得ai和aj呢?
对于ai,即第一个乘子,可以通过刚刚说的那几种不满足KKT的条件来找,第二个乘子aj可以找满足条件

…………………………………………………………………………(5)
b的更新:

在满足条件:
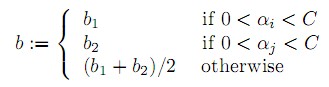
下更新b。……………(6)
最后更新所有ai,y和b,这样模型就出来了,然后通过函数:

……………………………………………………(7)
输入是x,是一个数组,组中每一个值表示一个特征。
输出是A类还是B类。(正类还是负类)
以下是主要的代码段:
[java] view plaincopyprint?
/*
* 默认输入参数值
* C: regularization parameter
* tol: numerical tolerance
* max passes
*/
double C = 1; //对不在界内的惩罚因子
double tol = 0.01;//容忍极限值
int maxPasses = 5; //表示没有改变拉格朗日乘子的最多迭代次数
/*
* 初始化a[], b, passes
*/
double a[] = new double[x.length];//拉格朗日乘子
this.a = a;
//将乘子初始化为0
for (int i = 0; i < x.length; i++) {
a[i] = 0;
}
int passes = 0;
while (passes < maxPasses) {
//表示改变乘子的次数(基本上是成对改变的)
int num_changed_alphas = 0;
for (int i = 0; i < x.length; i++) {
//表示特定阶段由a和b所决定的输出与真实yi的误差
//参照公式(7)
double Ei = getE(i);
/*
* 把违背KKT条件的ai作为第一个
* 满足KKT条件的情况是:
* yi*f(i) >= 1 and alpha == 0 (正确分类)
* yi*f(i) == 1 and 0<alpha < C (在边界上的支持向量)
* yi*f(i) <= 1 and alpha == C (在边界之间)
*
*
*
* ri = y[i] * Ei = y[i] * f(i) - y[i]^2 >= 0
* 如果ri < 0并且alpha < C 则违反了KKT条件
* 因为原本ri < 0 应该对应的是alpha = C
* 同理,ri > 0并且alpha > 0则违反了KKT条件
* 因为原本ri > 0对应的应该是alpha =0
*/
if ((y[i] * Ei < -tol && a[i] < C) ||
(y[i] * Ei > tol && a[i] > 0))
{
/*
* ui*yi=1边界上的点 0 < a[i] < C
* 找MAX|E1 - E2|
*/
int j;
/*
* boundAlpha表示x点处于边界上所对应的
* 拉格朗日乘子a的集合
*/
if (this.boundAlpha.size() > 0) {
//参照公式(5)
j = findMax(Ei, this.boundAlpha);
} else
//如果边界上没有,就随便选一个j != i的aj
j = RandomSelect(i);
double Ej = getE(j);
//保存当前的ai和aj
double oldAi = a[i];
double oldAj = a[j];
/*
* 计算乘子的范围U, V
* 参考公式(4)
*/
double L, H;
if (y[i] != y[j]) {
L = Math.max(0, a[j] - a[i]);
H = Math.min(C, C - a[i] + a[j]);
} else {
L = Math.max(0, a[i] + a[j] - C);
H = Math.min(0, a[i] + a[j]);
}
/*
* 如果eta等于0或者大于0 则表明a最优值应该在L或者U上
*/
double eta = 2 * k(i, j) - k(i, i) - k(j, j);//公式(3)
if (eta >= 0)
continue;
a[j] = a[j] - y[j] * (Ei - Ej)/ eta;//公式(2)
if (0 < a[j] && a[j] < C)
this.boundAlpha.add(j);
if (a[j] < L)
a[j] = L;
else if (a[j] > H)
a[j] = H;
if (Math.abs(a[j] - oldAj) < 1e-5)
continue;
a[i] = a[i] + y[i] * y[j] * (oldAj - a[j]);
if (0 < a[i] && a[i] < C)
this.boundAlpha.add(i);
/*
* 计算b1, b2
* 参照公式(6)
*/
double b1 = b - Ei - y[i] * (a[i] - oldAi) * k(i, i) - y[j] * (a[j] - oldAj) * k(i, j);
double b2 = b - Ej - y[i] * (a[i] - oldAi) * k(i, j) - y[j] * (a[j] - oldAj) * k(j, j);
if (0 < a[i] && a[i] < C)
b = b1;
else if (0 < a[j] && a[j] < C)
b = b2;
else
b = (b1 + b2) / 2;
num_changed_alphas = num_changed_alphas + 1;
}
}
if (num_changed_alphas == 0) {
passes++;
} else
passes = 0;
}
return new SVMModel(a, y, b);
/* * 默认输入参数值 * C: regularization parameter * tol: numerical tolerance * max passes */ double C = 1; //对不在界内的惩罚因子 double tol = 0.01;//容忍极限值 int maxPasses = 5; //表示没有改变拉格朗日乘子的最多迭代次数 /* * 初始化a[], b, passes */ double a[] = new double[x.length];//拉格朗日乘子 this.a = a; //将乘子初始化为0 for (int i = 0; i < x.length; i++) { a[i] = 0; } int passes = 0; while (passes < maxPasses) { //表示改变乘子的次数(基本上是成对改变的) int num_changed_alphas = 0; for (int i = 0; i < x.length; i++) { //表示特定阶段由a和b所决定的输出与真实yi的误差 //参照公式(7) double Ei = getE(i); /* * 把违背KKT条件的ai作为第一个 * 满足KKT条件的情况是: * yi*f(i) >= 1 and alpha == 0 (正确分类) * yi*f(i) == 1 and 0<alpha < C (在边界上的支持向量) * yi*f(i) <= 1 and alpha == C (在边界之间) * * * * ri = y[i] * Ei = y[i] * f(i) - y[i]^2 >= 0 * 如果ri < 0并且alpha < C 则违反了KKT条件 * 因为原本ri < 0 应该对应的是alpha = C * 同理,ri > 0并且alpha > 0则违反了KKT条件 * 因为原本ri > 0对应的应该是alpha =0 */ if ((y[i] * Ei < -tol && a[i] < C) || (y[i] * Ei > tol && a[i] > 0)) { /* * ui*yi=1边界上的点 0 < a[i] < C * 找MAX|E1 - E2| */ int j; /* * boundAlpha表示x点处于边界上所对应的 * 拉格朗日乘子a的集合 */ if (this.boundAlpha.size() > 0) { //参照公式(5) j = findMax(Ei, this.boundAlpha); } else //如果边界上没有,就随便选一个j != i的aj j = RandomSelect(i); double Ej = getE(j); //保存当前的ai和aj double oldAi = a[i]; double oldAj = a[j]; /* * 计算乘子的范围U, V * 参考公式(4) */ double L, H; if (y[i] != y[j]) { L = Math.max(0, a[j] - a[i]); H = Math.min(C, C - a[i] + a[j]); } else { L = Math.max(0, a[i] + a[j] - C); H = Math.min(0, a[i] + a[j]); } /* * 如果eta等于0或者大于0 则表明a最优值应该在L或者U上 */ double eta = 2 * k(i, j) - k(i, i) - k(j, j);//公式(3) if (eta >= 0) continue; a[j] = a[j] - y[j] * (Ei - Ej)/ eta;//公式(2) if (0 < a[j] && a[j] < C) this.boundAlpha.add(j); if (a[j] < L) a[j] = L; else if (a[j] > H) a[j] = H; if (Math.abs(a[j] - oldAj) < 1e-5) continue; a[i] = a[i] + y[i] * y[j] * (oldAj - a[j]); if (0 < a[i] && a[i] < C) this.boundAlpha.add(i); /* * 计算b1, b2 * 参照公式(6) */ double b1 = b - Ei - y[i] * (a[i] - oldAi) * k(i, i) - y[j] * (a[j] - oldAj) * k(i, j); double b2 = b - Ej - y[i] * (a[i] - oldAi) * k(i, j) - y[j] * (a[j] - oldAj) * k(j, j); if (0 < a[i] && a[i] < C) b = b1; else if (0 < a[j] && a[j] < C) b = b2; else b = (b1 + b2) / 2; num_changed_alphas = num_changed_alphas + 1; } } if (num_changed_alphas == 0) { passes++; } else passes = 0; } return new SVMModel(a, y, b);
运行后的结果还算可以吧,测试数据主要是用了libsvm的heart_scale的数据。
预测的正确率达到73%以上。
如果我把核函数从线性的改为基于RBF将会更好点。
最后,说到SVM算法实现包,应该有很多,包括svm light,libsvm,有matlab本身自带的svm工具包等。
另外,完整的代码,我将上传到CSDN下载地址上提供下载。
点击这里下载。
如理解有误敬请指正!谢谢!
我的邮箱:chen-hongqin@163.com
我的其他博客:
百度:http://hi.baidu.com/futrueboy/home
javaeye:http://futrueboy.javaeye.com/
CSDN: http://blog.csdn.net/techq
相关文章推荐
- 支持向量机(SVM)算法的Python实现
- Andrew Ng机器学习笔记+Weka相关算法实现(四)SVM和原始对偶问题
- 基于OpenCV的 SVM算法实现数字识别(三)---SMO求解
- 教你实现SVM算法(一)
- 支持向量机(SVM)算法的matlab的实现
- SVM算法实现(一)
- 手把手教你实现SVM算法(一)
- 支持向量机SVM算法应用【Python实现】
- SVM分类算法,libsvm的Java语言实现-根据语料和测试语料判断准确率的
- Andrew Ng机器学习笔记+Weka相关算法实现(六)SMO/LibSVM/SVM参数
- PK/NN/*/SVM:实现手写数字识别(数据集50000张图片)比较3种算法神经网络、灰度平均值、SVM各自的准确率—Jason niu
- 支持向量机(SVM)算法的matlab的实现
- 手把手教你实现SVM算法(一)
- 支持向量机(SVM)的SMO算法实现(Python)
- SVM实现之SMO算法
- 手把手教你实现SVM算法(一)
- 基于OpenCV的 SVM算法实现数字识别(四)---代码实现
- Andrew Ng机器学习笔记+Weka相关算法实现(四)SVM和原始对偶问题
- 手把手教你实现SVM算法(二)
- matlab体验svm算法【非实现】
