强连通分支算法--Tarjan算法和Gabow算法

Tarjan算法

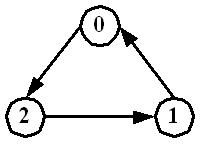
Kosaraju算法的流程简单，但是需要对图(和逆图)进行两次DFS搜索，而且读逆图的DFS搜索中顶点的访问顺序有特定的限制。下面将介绍的两个算法的过程比Kosaraju算法更为简洁，只需要执行一次DFS，并且不需要计算逆图。

Tarjan基于递归实现的深度优先搜索，在搜索过程中将顶点不断压入堆栈中，并在回溯时判断堆栈中顶点是否在同一联通分支。函数借助两个辅助数组pre和low，其中pre[u]为顶点u搜索的次序编号，low[u]为顶点u能回溯到的最早的顶点的次序编号。当pre[u]=low[u]时，则弹出栈中顶点并构成一个连通分支。以一个简单的例子来解释这一过程，如图所示，

	递归		回溯
栈	0	2	1
顶点	0	2	1	0	1	2	0
pre	0	1	2		2	1	0
low	0	1	2		0	0	0

寻找图中连通分支的过程

对图中的简单联通图，首先递归地对图进行深度优先搜索，并记录每个顶点的搜索次序pre。搜索起点为0，当对顶点1进行递归时将再次达到顶点0；在回溯过程中依次将顶点1和顶点2的low值修改为low[0]。当回溯到顶点0时将栈中low值为low[0]的顶点弹出并组成一个连通分支。

Tarjan算法实现如下：

/*

* Trajan 算法实现图的强连通区域求解；

* 算法步骤：

* @param G 待求解的图

* @return

* 一个二维单链表slk，单链表每个节点也是一个单链表，

* 每个节点处的单链表表示一个联通区域；

* slk的长度代表了图中联通区域的个数。

*/

public static SingleLink2 Tarjan(GraphLnk G){

SingleLink2 slk = new SingleLink2();

// 算法需借助于栈结构

LinkStack ls = new LinkStack();

int pre[] = new int[G.get_nv()];

int low[] = new int[G.get_nv()];

int cnt[] = new int[1];

// 初始化

for(int i = 0; i < G.get_nv(); i++){

pre[i] = -1;

low[i] = -1;

}

// 对顶点运行递归函数TrajanDFS

for(int i = 0; i < G.get_nv(); i++){

if(pre[i] == -1) {

GraphSearch.TarjanDFS(G,

i, pre, low, cnt,

ls, slk);

}

}

// 打印所有的联通区域

for(slk.goFirst(); slk.getCurrVal() != null; slk.next()){

// 获取一个链表元素项，即一个联通区域

GNodeSingleLink comp_i =

(GNodeSingleLink)(slk.getCurrVal().elem);

// 打印这个联通区域的每个图节点

for(comp_i.goFirst();

comp_i.getCurrVal() != null; comp_i.next()){

System.out.print(comp_i.getCurrVal().elem + "\t");

}

System.out.println();

}

return slk;

}

函数首先申明数组变量pre, low和cnt，并对初始化。pre 和low的意义前面已经解释过，cnt是长度为1的数组。因为在函数TarjanDFS中cnt的值需要不断变化，如果直接用变量作为形参，函数并不会改变cnt的值，所以需要使用数组。除了数组变量之外，还有一个栈ls，其作用是在对图进行深度优先搜索时记录遍历顶点，并在回溯时弹出部分顶点形成连通分支。

函数关键的步骤是对图中各顶点调用递归函数TarjanDFS，该函数以深度优先搜索算法为基础，在递归和回溯时不断对pre, low以及栈ls进行操作。实现如下：

/**

* Tarjan算法的递归DFS函数

*/

public static void TarjanDFS(GraphLnk G, int w,

int pre[], int low[], int cnt[],

LinkStack ls, SingleLink2 slk){

int t , min = low[w] = pre[w] = cnt[0]++;

// 将当前顶点号压栈

ls.push(new ElemItem<Integer>(w));

// 对当前顶点的每个邻点循环

for(Edge e = G.firstEdge(w);

G.isEdge(e);

e = G.nextEdge(e)){

// 如果邻点没有遍历过，则对其递归调用

if(pre[e.get_v2()] == -1){

TarjanDFS(G, e.get_v2(),

pre, low, cnt,

ls, slk);

}

/* 如果邻点已经被遍历过了，比较其编号与min,

* 如果编号较小，则更新min的大小*/

if(low[e.get_v2()] < min)

min = low[e.get_v2()];

}

// 如果此时min小于low[w]，则返回

if(min < low[w]){

low[w] = min;

return;

}

// 否则，弹出栈中元素，并将元素添加到链表中

GNodeSingleLink gnslk = new GNodeSingleLink();

do{

//弹出栈顶元素

t = ((Integer)(ls.pop().elem)).intValue();

low[t] = G.get_nv();

//添加到链表中

gnslk.append(new ElemItem<Integer>(t));

}while(t != w);

// 将该链表添加到slk链表中

slk.append(new ElemItem<GNodeSingleLink>(gnslk));

}

下面以图中有向图为例，分析Tarjan算法求解较为复杂的有向图的过程。各顶点的搜索访问次序以及low值的变化如图。

顶点	0	1	2	3	4	5	6	7	8	9
次序	0	2	1	3	6	4	7	5	8	9
low	0	2/0	1/0	3	6	4/3	7/6	5	8	9/8
min	0	2/0	1/0	3	6	4/3	7/6	5	8	9/8

深度优先搜索各顶点的访问次序以及堆栈中顶点的变化过程如图。其中框出来的步骤表示遍历到达已访问过的顶点，此时需要对low做修改，堆栈中黑体加粗的顶点表示弹出的顶点。



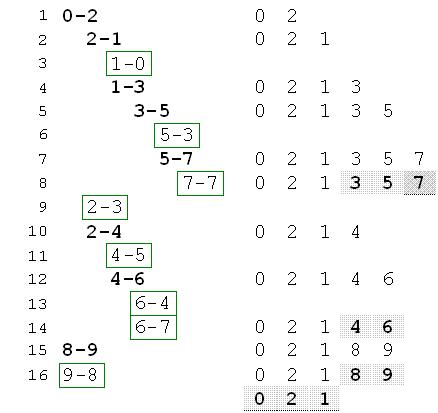
图 Tarjan算法详细过程图

算法详细过程分析如下：

搜索起点为顶点0，递归搜索顶点2、顶点1，这三个顶点被压入栈中。在顶点1处首先递归搜索顶点0，由于顶点0已经访问过，所以不再递归搜索顶点0，而是作如下处理：

如果low[0] < 顶点1的min（记为min1），则min1 ← low[0]，

此时(0=low[0])<(min1=1)，所以min1←0。

接着到达顶点3，顶点3尚未被访问，则递归搜索顶点3，并继续搜索顶点5。此时，顶点5第一个相邻点为顶点3，则不再递归搜索顶点3，更新min5值，min5←3。

接着递归搜索顶点7，顶点7只有一个相邻顶点，即为顶点自身，则顶点7的递归结束。回溯到顶点7，此时min7=low[7]=5，弹出栈中顶点7，并作为第一个联通分支。

函数继续回溯到顶点5，此时顶点5的相邻顶点的递归搜索已经全部结束，由于(3=min5)<(low[5]=5)，则low[5]←(min5=3)，并返回；函数回溯到顶点3，此时与顶点3相邻的顶点的递归搜索也已全部完成，由于min3=low[3]=3，所以弹出栈中顶点5和顶点3，作为第二个连通分支。

函数回溯至顶点1，此时与顶点1相邻的顶点的递归调用已结束，此时(0=min1)<(low[1]=2)，则low[1]←(min1=0)，并返回；函数回溯顶点2，更新min2←(low[1]=0)；此时顶点2还有两个相邻顶点，即顶点3和顶点4，顶点3已经判定属于第二个连通分支，所以对顶点4递归搜索。

首先将顶点4压入栈中，对相邻顶点5递归搜索，顶点5已经判定属于第二个连通分支，所以转而对顶点6递归搜索。顶点6的第一个相邻顶点为4，则不再递归搜索顶点4，更新顶点6的min6←(low[4]=6)。顶点6的第二个相邻顶点为7，但顶点7已经判定属于第一个连通分支。此时顶点6的所有相邻顶点递归搜索结束，此时(6=min6)<(low[6]=7)，则low[6]←(min6=6)，并返回；函数回溯到顶点4，与顶点4相邻的顶点的递归搜索也已全部完成，由于min4=low[4]=6，所以弹出栈中顶点6和顶点4，作为第三个连通分支。

函数回溯至顶点2，此时顶点2的所有相邻顶点递归搜索结束，此时(0=min2)<(low[2]=1)，则low[2]←(min2=0)，并返回；

函数回溯至顶点0，此时顶点0的所有相邻顶点递归搜索结束，并且顶点min0=low[0]，则将栈中顶点1,2,0依次弹出，作为第四个连通分支。

最后函数继续递归搜索顶点8和顶点9(略)。

从算法的流程可以清楚的发现Tarjan算法可以在线性时间内找出一个有向图的强分量，并且对原图进行一次DFS即可。

.Gabow算法

Gabow算法是Tarjan算法的提升版本，该算法类似于Tarjan算法。算法维护了一个顶点栈，但是还是用了第二个栈来确定何时从第一个栈中弹出各个强分支中的顶点，它的功能类似于Tarjan算法中的数组low。从起始顶点w处开始进行DFS过程中，当一条回路显示这组顶点都属于同一个强连通分支时，就会弹出栈二中顶点，只留下回边的目的顶点，也即搜索的起点w。

当回溯到递归起始顶点w时，如果此时该顶点在栈二顶部，则说明该顶点是一个强联通分量的起始顶点，那么在该顶点之后搜索的顶点都属于同一个强连通分支。于是，从第一个栈中弹出这些点，形成一个强连通分支。

根据上面对算法的描述，实现如下：

/* Gabow 算法实现图的强连通区域查找；

* @param G 输入为图结构

* @return:

* 函数最终返回一个二维单链表slk，单链表每个节点又是一个单链表，

* 每个节点处的单链表表示一个联通区域；

* slk的长度代表了图中联通区域的个数。

*/

public static SingleLink2 Gabow(GraphLnk G){

SingleLink2 slk = new SingleLink2();

// 函数使用两个堆栈

LinkStack ls = new LinkStack();

LinkStack P = new LinkStack();

int pre[] = new int[G.get_nv()];

int cnt[] = new int[1];

// 标注各个顶点所在的连通分支的名称

int id[] = new int[G.get_nv()];

// 初始化

for(int i = 0; i < G.get_nv(); i++){

pre[i] = -1;

id[i] = -1;

}

for(int i = 0; i < G.get_nv(); i++){

if(pre[i] == -1) {

GraphSearch.GabowDFS(G,

i, pre, id, cnt,

ls, P, slk);

}

}

//打印所有的联通区域

for(slk.goFirst(); slk.getCurrVal() != null; slk.next()){

//获取一个链表元素项，即一个联通区域

GNodeSingleLink comp_i =

(GNodeSingleLink)(slk.getCurrVal().elem);

//打印这个联通区域的每个图节点

for(comp_i.goFirst();

comp_i.getCurrVal() != null; comp_i.next()){

System.out.print(comp_i.getCurrVal().elem + "\t");

}

System.out.println();

}

return slk;

}

函数调用递归实现的深度优先搜索GabowDFS，实现如下：

/**

* GabowDFS算法的递归DFS函数

* @param ls 栈1,

* @param P 栈2，决定何时弹出栈1中顶点

*/

public static void GabowDFS(GraphLnk G, int w,

int pre[], int[] id, int cnt[],

LinkStack ls, LinkStack P,

SingleLink2 slk){

int v;

pre[w] = cnt[0]++;

//将当前顶点号压栈

ls.push(new ElemItem<Integer>(w));

System.out.print("+0 stack1 ");ls.printStack();

P.push(new ElemItem<Integer>(w));

System.out.print("+0 stack2 ");P.printStack();

// 对当前顶点的每个邻点循环

for(Edge e = G.firstEdge(w); G.isEdge(e); e = G.nextEdge(e)){

//如果邻点没有遍历过，则对其递归调用

if(pre[e.get_v2()] == -1){

GabowDFS(G, e.get_v2(), pre, id, cnt, ls, P, slk);

}

// 否则，如果邻点被遍历过但又没有被之前的连通域包含，则循环弹出

else if(id[e.get_v2()] == -1){

int ptop = ((Integer)(P.getTop().elem)).intValue();

// 循环弹出，直到栈顶顶点的序号不小于邻点的序号

while(pre[ptop] > pre[e.get_v2()]) {

P.pop();

System.out.print("-1 stack2 ");P.printStack();

ptop = ((Integer)(P.getTop().elem)).intValue();

}

}

}

// 遍历完顶点的所有相邻顶点后，如果栈2顶部顶点与w相同则弹出；

if(P.getTop() != null

&& ((Integer)(P.getTop().elem)).intValue() == w){

P.pop();

System.out.print("-2 stack2 ");P.printStack();

}

// 否则函数返回

else return;

// 如果栈2顶部顶点与w相同，则弹出栈1中顶点，形成连通分支

GNodeSingleLink gnslk = new GNodeSingleLink();

do{

v = ((Integer)(ls.pop().elem)).intValue();

id[v] = 1;

gnslk.append(new ElemItem<Integer>(v));

}while(v != w);

System.out.print("-3 stack1 ");ls.printStack();

slk.append(new ElemItem<GNodeSingleLink>(gnslk));

}

以图中有向图为例，并在深度优先搜索过程中跟踪记录两个栈中元素的变化如下：

+0 stack1 当前栈从栈顶至栈底元素为：

0.

+0 stack2 当前栈从栈顶至栈底元素为：

0.

+0 stack1 当前栈从栈顶至栈底元素为：

2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

2, 0.

+0 stack1 当前栈从栈顶至栈底元素为：

1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

1, 2, 0.

-1 stack2 当前栈从栈顶至栈底元素为：

2, 0.

-1 stack2 当前栈从栈顶至栈底元素为：

0.

+0 stack1 当前栈从栈顶至栈底元素为：

3, 1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

3, 0.

+0 stack1 当前栈从栈顶至栈底元素为：

5, 3, 1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

5, 3, 0.

-1 stack2 当前栈从栈顶至栈底元素为：

3, 0.

+0 stack1 当前栈从栈顶至栈底元素为：

7, 5, 3, 1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

7, 3, 0.

-2 stack2 当前栈从栈顶至栈底元素为：

3, 0.

-3 stack1 当前栈从栈顶至栈底元素为：

5, 3, 1, 2, 0.

-2 stack2 当前栈从栈顶至栈底元素为：

0.

-3 stack1 当前栈从栈顶至栈底元素为：

1, 2, 0.

+0 stack1 当前栈从栈顶至栈底元素为：

4, 1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

4, 0.

+0 stack1 当前栈从栈顶至栈底元素为：

6, 4, 1, 2, 0.

+0 stack2 当前栈从栈顶至栈底元素为：

6, 4, 0.

-1 stack2 当前栈从栈顶至栈底元素为：

4, 0.

-2 stack2 当前栈从栈顶至栈底元素为：

0.

-3 stack1 当前栈从栈顶至栈底元素为：

1, 2, 0.

-2 stack2 当前栈为空！

-3 stack1 当前栈为空！

+0 stack1 当前栈从栈顶至栈底元素为：

8.

+0 stack2 当前栈从栈顶至栈底元素为：

8.

+0 stack1 当前栈从栈顶至栈底元素为：

9, 8.

+0 stack2 当前栈从栈顶至栈底元素为：

9, 8.

-1 stack2 当前栈从栈顶至栈底元素为：

8.

-2 stack2 当前栈为空！

算法的流程这里不做详细分析，读者可以参见Tarjan算法的分析流程，并自行体会算法的思想。