基础学习笔记——Recall, Precision, and Average Precision

以下内容绝大部分内容翻译自：

Mu Zhu , Recall, Precision, and Average Precision. Working Paper 2004-09 Department of Statistics & Actuarial Science University of Waterloo.

1. 先介绍一些基础内容和符号说明



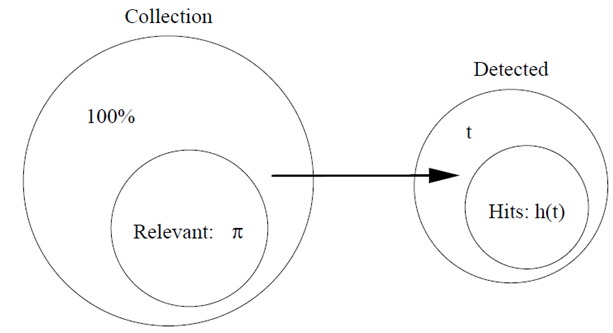
C：一个很大item的集合。

π：集合中相关的item的集合（π<< 1）。

t：算法所识别出的item的集合。

h(t)：t中确实相关的item的集合，通常这部分称作命中（相反的是丢失）

下面看一些典型的“命中”曲线



假设其中相关item为5%。

hP(t)曲线是理想的曲线，几乎排在前面的所有的识别都命中了，直到5%，所有的相关item都耗尽了，曲线不再变化。

hR(t)曲线是随机选择的曲线

hA(t)和hB(t)是典型的识别曲线

（两条曲线相交是可能的）

“命中曲线”能够很清楚地告诉我们一个模型或者是算法的性能好坏。例如，如果在任何时候，有 hA(t)>hB(t)，则算法A毫无疑问比算法B出色；如果一般情况下，一条曲线总是随着t的增长而快速增长，则这个算法被认为是强壮的；特别的，一个最好的算法应该拥有最大地斜率，直到 t=π。

然而，我们需要的不仅是对算法好坏的评估和比较，而是要往好的方面来调整算法。经常，我们需要半人工地来产生一些算法的最优经验参数就像交叉验证。举例来说，对于

K - nearest-neighbor算法，我们必须选择最合适的K，然后通过交叉验证找出出色的值。因此，我们可以看到，我们更为需要的是一个评估值，而不是一条曲线。

两个数值化的评估方法通常是：recall和precision

2. 简单介绍 Recall 和 Precision

简单定义：

Recall：在所有item中识别出相关item的概率。

Precision：在算法所识别出的item中，真正相关的概率。

形式化定义：

设 ω 是集合 C 中随机取出的一个元素



则



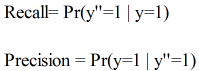
或者可以表示成



3. Recall 和 Precision 之间的关系

引理1：



证明： 根据贝叶斯公式，可以得到：



注意：在这里，我们将Precision和Recall都看作是关于自变量 t 的函数，因为一般来说，随着 t 的变化，算法的一些表现也会跟着变化。

h(t) , r(t) , p(t) 都看作是连续光滑的曲线，因为集合C足够大。

引理2：

1. r(0) = 0 r(1) = 1

2. r'(t) >= 0 （t∈[0,1]）

证明：

1. 显然，当 t = 0 时，Recall必然为0，因为没有item被检测；

当 t = 1 时，Recall必然等于1，因为所有的item都被检测了，那么也必定包括所有相关的item；

2. 显然，r (t+△t) > r(t) 或者 r (t+△t) = r(t)

所以，r (t+△t) >= r(t)

假设 t 在几乎任何一点都可导，则有：


所以 r'(t)
>= 0 （ t∈[0,1] ）

引理2说明了 r(t) 是一个非递减函数，而且对于一个典型的识别算法来说，一般都有 r''(t) <= 0，即识别率是渐渐减缓的，直观上来说

随着 t 的上升，识别变得越来越困难。

假设1：假设 r(t) 是二次可微函数，则 r''(t) <= 0 , t∈[0,1].

引理3：假设 p(t) 可微，若假设1成立，则 p'(t)<= 0 , t∈[0,1].

证明：





根据中值定理，存在 S ∈[0,t].

使得 r(t) - r(0) = r'(s) (t - 0)

∵ r(0) = 0;

∴ r(t) = r'(s)t

又根据假设1， 有 r''(t) <= 0

所以 r'(s) >= r'(t) （s<=t）

所以 r'(s)t >= r'(t)t

即 r(t) >= r'(t)t

则 p'(t) <= 0

根据之前所证明的，r'(t) >= 0，可以看出，Recall和Precision的确存在某些相互影响的关系。

（此证明基于假设1，r(t)的二阶导数小于等于0，即r''(t)是凸函数）



所以说，单用这两个之中的某一个来评估和比较都不太合适，下面介绍的AP将会同时考虑Recall和Precision，因此常被用来作为衡量和评估的标准。

4. Average Precision（AP）

首先，Precision能被表示成Recall的函数，p(r), 因为 p(t) = π*r(t)/t ，具体见上所述。

AP的定义如下：



引理4：设r(t)可微函，则：





某些情况下，AP并不怎么直观，当 r'(t) = 0时，p(t)必然decreasing in t （无论在哪个区间内）

上面这句话不是特别理解。。。。

然而，因为dr为0，那么AP无论如何不会在此区间内发生变化。

下面举一些例子：

1. Random Selection：

假设 h(t) = π*t，即相关的比例在所有识别的比例中保持为 π

则 r(t) = h(t)/π = t

此时：AP = π

2. Perfect Detection:

h(t)= t [0,π]

h(t)=π (π,1]

这说明：前π个识别，全部命中，即h(t) = t，当π被耗尽时，h(t) = π,保持不变

这是最理想识别，也说明：

r(t) = t/π [0,π]

r(t) = 1 (π,1]

此时的AP = 1；

3. 实际应用中：

假设有n个测试item，将他们根据置信度又高到底排列后，计算：





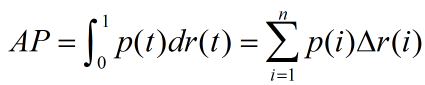
其中，△r(i)表示后一次识别后，recall的变化量，

p(i)可表示为：R/i ，其中R前i个item中，相关的item个数。

因此AP也可表示为：



其中，R表示测试集所有的relavant的item个数；

n表示测试集中item的数量；

Ij = 1，如果第j个item相关，否则，Ij = 0；

Rj，前j个item中，相关的item个数；

下面看个例子：

假设这些item的置信度已经由高到底排列：







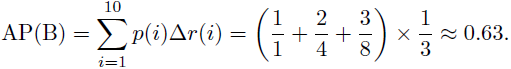
因此，算法A好于算法B。

由此也可以看出，AP这个衡量标准更偏爱识别得早的算法。

后略。

希望大家帮忙改正。