Laplacian matrix

转自：http://en.wikipedia.org/wiki/Laplacian_matrix

In the mathematical field
of graph theory the Laplacian
matrix, sometimes called admittance matrix or Kirchhoff
matrix, is a matrixrepresentation
of a graph.
Together with Kirchhoff's theorem it
can be used to calculate the number of spanning
trees for a given graph. The Laplacian matrix can be used to find many other properties of the graph; see spectral
graph theory. Cheeger's
inequality from Riemannian Geometry has a discrete analogue involving the Laplacian Matrix; this is perhaps the most important theorem in Spectral Graph theory and one
of the most useful facts in algorithmic applications. It approximates the sparsest cut of a graph through the second eigenvalue of its Laplacian.

Definition

Given a simple graph G with n vertices, its Laplacian matrix

is
defined as:[1]



That is, it is the difference of the degree matrix D and the adjacency
matrix A of the graph. In the case of directed graphs, either the indegree
or outdegree might be used, depending on the application.

From the definition follows that:



where deg(vi) is degree of the vertex i.

The normalized Laplacian matrix is defined as:[1]

Example

Here is a simple example of a labeled graph and its Laplacian matrix.

Labeled graph	Laplacian matrix

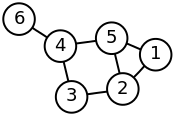[edit]Properties

For a graph G and its Laplacian matrix L with eigenvalues

:

L is always positive-semidefinite (

).
The number of times 0 appears as an eigenvalue in the Laplacian is the number of connected
components in the graph.
L is an M-matrix.


is always 0 because every Laplacian matrix has an eigenvector

that,
for each row, adds the corresponding node's degree (from the diagonal) to a "-1" for each neighbor so that


The smallest non-zero eigenvalue of L is called the spectral gap.
If we define an oriented incidence matrix M with element Mev for edge e (connecting vertex i and j, with i < j) and vertex v given
by



then the Laplacian matrix L satisfies



where

is the matrix
transpose of M.

The second smallest eigenvalue of L is the algebraic connectivity (or Fiedler
value) of G.

[edit]Deformed
Laplacian

The deformed Laplacian is commonly defined as



where I is the unit matrix, A is the adjacency matrix, and D is the degree matrix, and s is a (complex-valued) number. Note that normal Laplacian is just

.

[edit]As
a matrix representation of the negative discrete Laplace operator

The Laplacian matrix can be interpreted as a matrix representation of a particular case of the negative discrete
Laplace operator. Such an interpretation allows one, e.g., to generalise the Laplacian matrix to the case of graphs with an infinite number of vertices and edges, leading to a Laplacian matrix of an infinite size.

[edit]As
an approximation to the negative continuous Laplacian

The graph Laplacian matrix can be further viewed as a matrix form of an approximation to the negative Laplacian operator
obtained by the finite difference method[citation
needed]. In this interpretation, every graph vertex is treated as a grid point; the local connectivity of the vertex determines the finite difference approximation stencil at
this grid point, the grid size is always one for every edge, and there are no constraints on any grid points, which corresponds to the case of the homogeneous Neumann
boundary condition, i.e., free boundary.