很牛的牛顿迭代法
2011-12-26 22:33
204 查看
在MIT公开课《计算机科学与编程导论》的第五讲中,讲到编写求解平方根的函数sqrt时,提到了牛顿迭代法。今天仔细一查,发现这是一个用途很广、很牛的计算方法。
首先,考虑如何编写一个开平方根的函数sqrt(float num, float e)。参数num是要求开平方根的实数,参数e是计算结果可以达到多大误差。这是一个无法得到精确解,只能求出近似解的问题。该如何编写呢?
1. 传统的二分法
我们可以先猜测一个值作为解,看这个值是否在误差范围内。如果没有达到误差要求,就构造一个更好的猜测值,继续迭代。猜测值可以简单地初始化为num/2,但怎样在下一轮迭代前构造一个更好的猜测值呢?我们不妨参照二分查找算法的思路,解的初始范围是[0, num],用二分法逐渐缩小范围。
private static float sqrt(float num, float e)
{
[align=left] [/align]
float low
= 0F;
float high
= num;
float guess,
e0;
int count
= 0;
[align=left] [/align]
[align=left] do {[/align]
[align=left] guess = (low + high) / 2;[/align]
if (guess*guess
> num) {
[align=left] high = guess;[/align]
[align=left] e0 = guess*guess - num;[/align]
[align=left] } else {[/align]
[align=left] low = guess;[/align]
[align=left] e0 = num - guess*guess;[/align]
[align=left] }[/align]
[align=left] [/align]
[align=left] count++;[/align]
System.out.printf("Try
%f, e: %f\n", guess, e0);
} while (e0
> e);
System.out.printf("Try
%d times, result: %f\n", count, guess);
[align=left] [/align]
[align=left] return guess;[/align]
[align=left] }[/align]
在区间[low, high]内取中点(low+high)/2作为猜测值。如果guess*guess大于num,说明猜测值偏大,则在区间[low, guess]进行下一轮迭代,否则在区间[guess, high]中继续。当误差值e0小于能够接受的误差值e时停止迭代,返回结果。
取num=2, e=0.01进行测试,运行结果如下:
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 8 times, result: 1.414063[/align]
可见尝试了八次才达到0.01的误差。
2. 神奇的牛顿法
仔细思考一下就能发现,我们需要解决的问题可以简单化理解。
从函数意义上理解:我们是要求函数f(x) = x²,使f(x) = num的近似解,即x² - num = 0的近似解。
从几何意义上理解:我们是要求抛物线g(x) = x² - num与x轴交点(g(x) = 0)最接近的点。
我们假设g(x0)=0,即x0是正解,那么我们要做的就是让近似解x不断逼近x0,这是函数导数的定义:
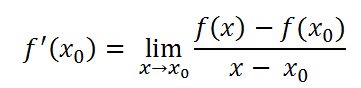

可以由此得到
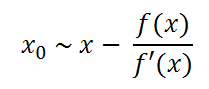
.png)
从几何图形上看,因为导数是切线,通过不断迭代,导数与x轴的交点会不断逼近x0。
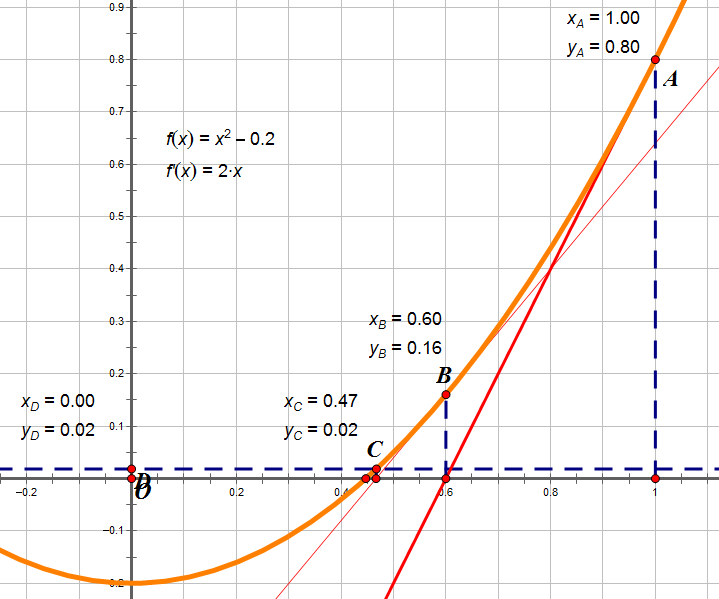
3. 牛顿法的实现与测试
public static void main(String[]
args) {
float num
= 2;
float e
= 0.01F;
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] [/align]
[align=left] num = 2;[/align]
[align=left] e = 0.0001F;[/align]
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] [/align]
[align=left] num = 2;[/align]
[align=left] e = 0.00001F;[/align]
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] }[/align]
private static float sqrtNewton(float num, float e)
{
[align=left] [/align]
float guess
= num / 2;
[align=left] float e0;[/align]
int count
= 0;
[align=left] [/align]
[align=left] do {[/align]
[align=left] guess = (guess + num / guess) / 2;[/align]
[align=left] e0 = guess*guess - num;[/align]
[align=left] [/align]
[align=left] count++;[/align]
System.out.printf("Try
%f, e: %f\n", guess, e0);
} while (e0
> e);
System.out.printf("Try
%d times, result: %f\n", count, guess);
[align=left] [/align]
[align=left] return guess;[/align]
[align=left] }[/align]
与二分法的对比测试结果:
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 8 times, result: 1.414063[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 2 times, result: 1.416667[/align]
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 1.417969, e: 0.010635[/align]
[align=left]Try 1.416016, e: 0.005100[/align]
[align=left]Try 1.415039, e: 0.002336[/align]
[align=left]Try 1.414551, e: 0.000954[/align]
[align=left]Try 1.414307, e: 0.000263[/align]
[align=left]Try 1.414185, e: 0.000082[/align]
[align=left]Try 14 times, result: 1.414185[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 1.414216, e: 0.000006[/align]
[align=left]Try 3 times, result: 1.414216[/align]
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 1.417969, e: 0.010635[/align]
[align=left]Try 1.416016, e: 0.005100[/align]
[align=left]Try 1.415039, e: 0.002336[/align]
[align=left]Try 1.414551, e: 0.000954[/align]
[align=left]Try 1.414307, e: 0.000263[/align]
[align=left]Try 1.414185, e: 0.000082[/align]
[align=left]Try 1.414246, e: 0.000091[/align]
[align=left]Try 1.414215, e: 0.000004[/align]
[align=left]Try 16 times, result: 1.414215[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 1.414216, e: 0.000006[/align]
[align=left]Try 3 times, result: 1.414216[/align]
可以看到随着对误差要求的更加精确,二分法的效率很低下,而牛顿法的确非常高效。
可在两三次内得到结果。
如果搞不清牛顿法的具体原理,可能就要像我一样复习下数学知识了。极限、导数、泰勒展开式、单变量微分等。
4. 更快的方法
在Quake源码中有段求sqrt的方法,大概思路是只进行一次牛顿迭代,得到能够接受误差范围内的结果。
因此肯定是更快的。
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df -
( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
参考文章
Quake3源码中的sqrt http://www.matrix67.com/blog/archives/362
牛顿迭代方程的近似解 http://blueve.me/archives/369
首先,考虑如何编写一个开平方根的函数sqrt(float num, float e)。参数num是要求开平方根的实数,参数e是计算结果可以达到多大误差。这是一个无法得到精确解,只能求出近似解的问题。该如何编写呢?
1. 传统的二分法
我们可以先猜测一个值作为解,看这个值是否在误差范围内。如果没有达到误差要求,就构造一个更好的猜测值,继续迭代。猜测值可以简单地初始化为num/2,但怎样在下一轮迭代前构造一个更好的猜测值呢?我们不妨参照二分查找算法的思路,解的初始范围是[0, num],用二分法逐渐缩小范围。
private static float sqrt(float num, float e)
{
[align=left] [/align]
float low
= 0F;
float high
= num;
float guess,
e0;
int count
= 0;
[align=left] [/align]
[align=left] do {[/align]
[align=left] guess = (low + high) / 2;[/align]
if (guess*guess
> num) {
[align=left] high = guess;[/align]
[align=left] e0 = guess*guess - num;[/align]
[align=left] } else {[/align]
[align=left] low = guess;[/align]
[align=left] e0 = num - guess*guess;[/align]
[align=left] }[/align]
[align=left] [/align]
[align=left] count++;[/align]
System.out.printf("Try
%f, e: %f\n", guess, e0);
} while (e0
> e);
System.out.printf("Try
%d times, result: %f\n", count, guess);
[align=left] [/align]
[align=left] return guess;[/align]
[align=left] }[/align]
在区间[low, high]内取中点(low+high)/2作为猜测值。如果guess*guess大于num,说明猜测值偏大,则在区间[low, guess]进行下一轮迭代,否则在区间[guess, high]中继续。当误差值e0小于能够接受的误差值e时停止迭代,返回结果。
取num=2, e=0.01进行测试,运行结果如下:
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 8 times, result: 1.414063[/align]
可见尝试了八次才达到0.01的误差。
2. 神奇的牛顿法
仔细思考一下就能发现,我们需要解决的问题可以简单化理解。
从函数意义上理解:我们是要求函数f(x) = x²,使f(x) = num的近似解,即x² - num = 0的近似解。
从几何意义上理解:我们是要求抛物线g(x) = x² - num与x轴交点(g(x) = 0)最接近的点。
我们假设g(x0)=0,即x0是正解,那么我们要做的就是让近似解x不断逼近x0,这是函数导数的定义:
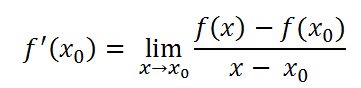

可以由此得到
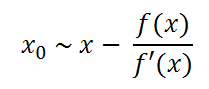
.png)
从几何图形上看,因为导数是切线,通过不断迭代,导数与x轴的交点会不断逼近x0。

3. 牛顿法的实现与测试
public static void main(String[]
args) {
float num
= 2;
float e
= 0.01F;
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] [/align]
[align=left] num = 2;[/align]
[align=left] e = 0.0001F;[/align]
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] [/align]
[align=left] num = 2;[/align]
[align=left] e = 0.00001F;[/align]
[align=left] sqrt(num, e);[/align]
[align=left] sqrtNewton(num, e);[/align]
[align=left] }[/align]
private static float sqrtNewton(float num, float e)
{
[align=left] [/align]
float guess
= num / 2;
[align=left] float e0;[/align]
int count
= 0;
[align=left] [/align]
[align=left] do {[/align]
[align=left] guess = (guess + num / guess) / 2;[/align]
[align=left] e0 = guess*guess - num;[/align]
[align=left] [/align]
[align=left] count++;[/align]
System.out.printf("Try
%f, e: %f\n", guess, e0);
} while (e0
> e);
System.out.printf("Try
%d times, result: %f\n", count, guess);
[align=left] [/align]
[align=left] return guess;[/align]
[align=left] }[/align]
与二分法的对比测试结果:
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 8 times, result: 1.414063[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 2 times, result: 1.416667[/align]
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 1.417969, e: 0.010635[/align]
[align=left]Try 1.416016, e: 0.005100[/align]
[align=left]Try 1.415039, e: 0.002336[/align]
[align=left]Try 1.414551, e: 0.000954[/align]
[align=left]Try 1.414307, e: 0.000263[/align]
[align=left]Try 1.414185, e: 0.000082[/align]
[align=left]Try 14 times, result: 1.414185[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 1.414216, e: 0.000006[/align]
[align=left]Try 3 times, result: 1.414216[/align]
[align=left]Try 1.000000, e: 1.000000[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.250000, e: 0.437500[/align]
[align=left]Try 1.375000, e: 0.109375[/align]
[align=left]Try 1.437500, e: 0.066406[/align]
[align=left]Try 1.406250, e: 0.022461[/align]
[align=left]Try 1.421875, e: 0.021729[/align]
[align=left]Try 1.414063, e: 0.000427[/align]
[align=left]Try 1.417969, e: 0.010635[/align]
[align=left]Try 1.416016, e: 0.005100[/align]
[align=left]Try 1.415039, e: 0.002336[/align]
[align=left]Try 1.414551, e: 0.000954[/align]
[align=left]Try 1.414307, e: 0.000263[/align]
[align=left]Try 1.414185, e: 0.000082[/align]
[align=left]Try 1.414246, e: 0.000091[/align]
[align=left]Try 1.414215, e: 0.000004[/align]
[align=left]Try 16 times, result: 1.414215[/align]
[align=left]Try 1.500000, e: 0.250000[/align]
[align=left]Try 1.416667, e: 0.006945[/align]
[align=left]Try 1.414216, e: 0.000006[/align]
[align=left]Try 3 times, result: 1.414216[/align]
可以看到随着对误差要求的更加精确,二分法的效率很低下,而牛顿法的确非常高效。
可在两三次内得到结果。
如果搞不清牛顿法的具体原理,可能就要像我一样复习下数学知识了。极限、导数、泰勒展开式、单变量微分等。
4. 更快的方法
在Quake源码中有段求sqrt的方法,大概思路是只进行一次牛顿迭代,得到能够接受误差范围内的结果。
因此肯定是更快的。
float Q_rsqrt( float number )
{
long i;
float x2, y;
const float threehalfs = 1.5F;
x2 = number * 0.5F;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df -
( i >> 1 ); // what the fuck?
y = * ( float * ) &i;
y = y * ( threehalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threehalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
#ifndef Q3_VM
#ifdef __linux__
assert( !isnan(y) ); // bk010122 - FPE?
#endif
#endif
return y;
}
参考文章
Quake3源码中的sqrt http://www.matrix67.com/blog/archives/362
牛顿迭代方程的近似解 http://blueve.me/archives/369
相关文章推荐
- 牛顿迭代法在求解三次方程上的应用
- 利用牛顿迭代法求平方根
- 牛顿迭代法
- 牛顿迭代法和最小二乘法直线拟合代码
- 牛顿迭代法
- 牛顿迭代法
- 牛顿迭代法
- 牛顿迭代法解非线性方程组(MATLAB版)
- 牛顿迭代法实现平方根函数sqrt
- 用牛顿迭代法求某正数n的平方根
- 牛顿迭代法
- sqrt()平方根计算函数的实现2——牛顿迭代法
- 【SPOJ-TRIGALGE】Easy Calculation【二分法】【牛顿迭代法】
- Java练习:牛顿迭代法 Vs. 不动点
- 牛顿迭代法(Newton's Method)
- 第十一周oj题目牛顿迭代法求根
- 牛顿迭代法和线性近似
- 牛顿迭代法求开根号。 a^1/2_______Xn+1=1/2*(Xn+a/Xn)
- 牛顿迭代法改造!!!!
- HDU 2199 Can you solve this equation? 牛顿迭代法 || 二分
