平衡二叉树(AVL树)的基本操作(附有示意图)
2011-08-10 19:30
531 查看
平衡二叉树关于树的深度是平衡的,具有较高的检索效率。平衡二叉树或是一棵空树,或是具有下列性质的二叉排序树:其左子树和右子树都是平衡二叉树,而且左右子树深度之差绝对值不超过1. 由此引出了平衡因子(balance factor)的概念,bf定义为该结点的左子树的深度减去右子树的深度(有些书是右子树深度减去左子树深度,我是按照左子树减去右子树来计算的,下面的代码也是这样定义的),所以平衡二叉树的结点的平衡因子只可能是 -1,0,1 ,某个结点的平衡因子绝对值大于1,该二叉树就不平衡。
平衡二叉树在出现不平衡状态的时候,要进行平衡旋转处理,有四种平衡旋转处理(单向右旋处理,单向左旋处理,双向旋转(先左后右)处理,双向旋转(先右后左)处理),归根到底是两种(单向左旋处理和单向右旋处理)。
文件"tree.h"
测试结果
下面是四种旋转的示意图
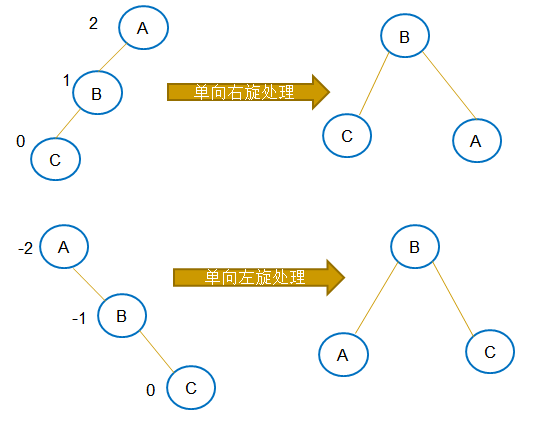
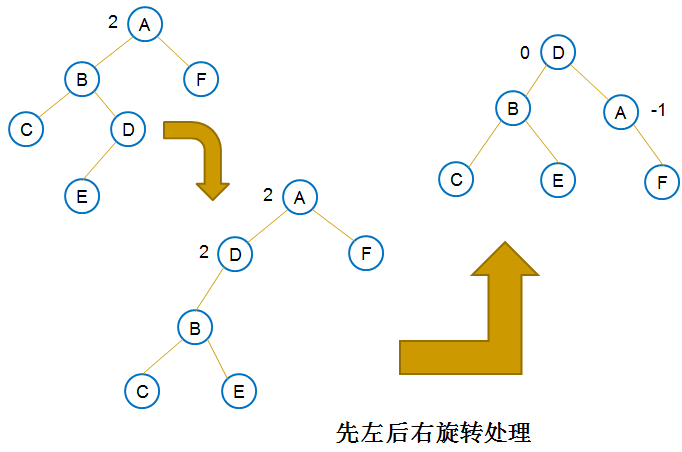
先右后左的和先左后右的相对应的 所以不画了 下面再画一个建树的过程 就不画了 太费时间了画这个 刚好找到一个画好的 直接贴
因为下面图中它的计算平衡因子的方式是右子树高度减去左子树高度,所以和我上面的计算方法相反,不过不影响观看
建立含有元素 16 3 7 11 9 26 18 14 15 的平衡二叉树的过程如下所示:

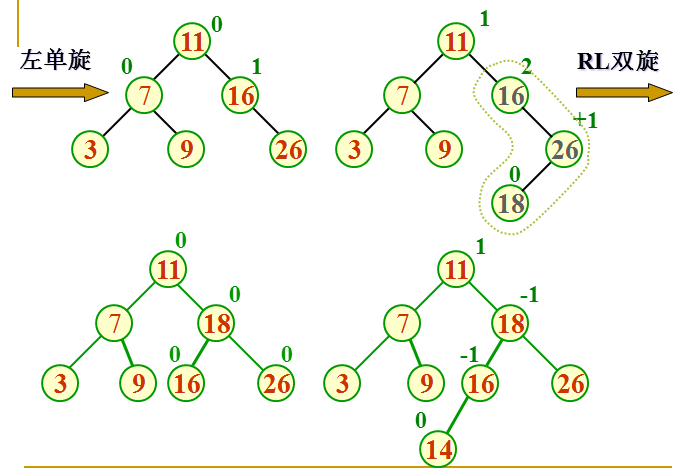

平衡二叉树在出现不平衡状态的时候,要进行平衡旋转处理,有四种平衡旋转处理(单向右旋处理,单向左旋处理,双向旋转(先左后右)处理,双向旋转(先右后左)处理),归根到底是两种(单向左旋处理和单向右旋处理)。
文件"tree.h"
#include<iostream>
#include<stack>
#include<queue>
using namespace std;
const int LH=1; //左子树比右子树高1
const int EH=0; //左右子树一样高
const int RH=-1;//右子树比左子树高1
const int MAX_NODE_NUM=20; //结点数目上限
class AVL_Tree;
class AvlNode
{
int data;
int bf; //平衡因子
AvlNode *lchild;
AvlNode *rchild;
friend class AVL_Tree;
};
class AVL_Tree
{
public:
int Get_data(AvlNode *p)
{
return p->data;
}
void Create_AVl(AvlNode *&T) //建树
{
cout<<"输入平衡二叉树的元素,输入-1代表结束输入:";
int num[MAX_NODE_NUM];
int a,i=0;
while(cin>>a && a!=-1)
{
num[i]=a;
i++;
}
if(num[0]==-1)
{
cout<<"平衡树为空"<<endl;
T=NULL;
return;
}
int k=i;
bool taller=false;
for(i=0;i<k;i++)
Insert_Avl(T,num[i],taller);//逐个进行插入,插入过程看下面的示意图
cout<<"_____建树完成____"<<endl;
}
void L_Rotate(AvlNode *&p)
{
//以p为根节点的二叉排序树进行单向左旋处理
AvlNode *rc=p->rchild;
p->rchild=rc->lchild;
rc->lchild=p;
p=rc;
}
void R_Rotate(AvlNode *&p)
{
//以p为根节点的二叉排序树进行单向右旋处理
AvlNode *lc=p->lchild;
p->lchild=lc->rchild;
lc->rchild=p;
p=lc;
}
void Left_Balance(AvlNode *&T)
{
//以T为根节点的二叉排序树进行左平衡旋转处理
AvlNode *lc,*rd;
lc=T->lchild;
switch(lc->bf)
{
case LH:
//新结点插在T的左孩子的左子树上,做单向右旋处理
T->bf=lc->bf=EH;
R_Rotate(T);
break;
case RH:
//新结点插在T的左孩子的右子树上,要进行双旋平衡处理(先左后右)
rd=lc->rchild;
switch(rd->bf)
{
case LH:
//插在右子树的左孩子上
T->bf=RH;
lc->bf=EH;
break;
case EH:
T->bf=lc->bf=EH;
break;
case RH:
T->bf=EH;
lc->bf=LH;
break;
}
rd->bf=EH;
L_Rotate(T->lchild);//先对T的左子树进行单向左旋处理
R_Rotate(T); //再对T进行单向右旋处理
}
}
void Right_Balance(AvlNode *&T)
{
//以T为根节点的二叉排序树进行右平衡旋转处理
AvlNode *rc,*ld;
rc=T->rchild;
switch(rc->bf)
{
case RH:
//新结点插在右孩子的右子树上,进行单向左旋处理
T->bf=rc->bf=EH;
L_Rotate(T);
break;
case LH:
//新结点插在T的右孩子的左子树上,要进行右平衡旋转处理(先右再左)
ld=rc->lchild;
switch(ld->bf)
{
case LH:
T->bf=LH;
rc->bf=EH;
break;
case EH:
T->bf=rc->bf=EH;
break;
case RH:
T->bf=EH;
rc->bf=RH;
break;
}
ld->bf=EH;
R_Rotate(T->rchild);//先对T的右子树进行单向右旋处理
L_Rotate(T); //再对T进行单向左旋处理
}
}
bool Insert_Avl(AvlNode *&T,int num,bool &taller) //插入
{
//若在平衡二叉树中不存在结点值和num一样大小的结点
//则插入值为num的新结点,并返回true
//若因为插入而使得二叉排序树失去平衡,则做平衡旋转处理
//taller反映树是否长高
if(!T)
{
//插入新结点,树长高,taller为true
T=new AvlNode;
T->data=num;
T->lchild=T->rchild=NULL;
T->bf=EH;
taller=true;
}
else
{
if(num==T->data)
{
//不重复插入
taller=false;
return false;
}
if(num<T->data) //继续在T的左子树中进行搜索
{
if(!Insert_Avl(T->lchild,num,taller))//插入不成功
return false;
if(taller) //已插入T的左子树,且左子树长高
{
switch(T->bf)
{
case LH:
/*—————————————————————
/ 插入前左子树高于右子树,需要进行做平衡处理
/ 不管是单向左旋处理,还是先左后右平衡处理
/ 处理结果都是使得插入新结点后,树的高度不变
/—————————————————————*/
Left_Balance(T);
taller=false;
break;
case EH:
//插入前左右子树等高,现在插入新街点后,左子树比右子树高
T->bf=LH;
taller=true;
break;
case RH:
//插入前右子树比左子树高,现在新结点插入左子树后,树变为左右子树等高
T->bf=EH;
taller=false;
break;
}
}
}
else
{
//num>T->data 在T的右子树中继续搜索
if(!Insert_Avl(T->rchild,num,taller))
return false;
if(taller)
{
switch(T->bf)
{
case LH:
//插入前左子树比右子树高,现在插入T的右子树后,左右子树等高
T->bf=EH;
taller=false;
break;
case EH:
//插入前左右子树等高,现在插入后,右子树比左子树高
T->bf=RH;
taller=true;
break;
case RH:
//插入前右子树比坐子树高,插入后,排序树失去平衡,需要进行右平衡处理
Right_Balance(T);
taller=false;
break;
}
}
}
}
return true;
}
bool Search_Avl(AvlNode *T,int num,AvlNode *&f,AvlNode *&p) //搜索
{
//用p带回查找到的顶点的地址,f带回p的双亲结点
p=T;
while(p)
{
if(p->data==num)
return true;
if(p->data>num)
{
f=p;
p=p->lchild;
}
else
{
f=p;
p=p->rchild;
}
}
return false;
}void Delete_AVL(AvlNode *&T,int num) //删除,删除后没有回溯到根节点,算法有错,待日后修改完善,有心的朋友可以自己加一个栈或者其他方式来实现
{
/*---------------------------------------------------------
/ 从树中删除一个节点后,要保证删后的树还是一棵平衡二叉树,
/ 删除前,首先是在树中查找是否有这个结点,用p指向该结点,
/ 用f指向p的双亲结点,这个结点在树中的位置有下面四种情况:
/
/ 1:如果p指向的结点是叶子结点,那么直接将f指针的左子树或者
/ 右子树置空,然后删除p结点即可。
/
/ 2:如果p指向的结点是只有左子树或右子树,那么只需要让p结点
/ 原来在f中的位置(左子树或右子树)用p的子树代替即可。
/ 代替后,要修改f的平衡因子,在失去平衡的时候,要调用相应的
/ 做平衡旋转或右平衡旋转进行恢复.
/
/ 3:如果p所指向的结点是根节点,那么直接将根节点置空
/
/ 4:如果p所指向的结点左右子树都非空,为了删除p后原序列的顺
/ 序不变,就需要在原序列中先找出p的直接前驱(或者直接后继)
/ 结点用那个结点的值来代替p结点的值,然后再删掉那个直接前
/ 驱(或者直接后继)结点。
/ 其中s指向的是要删除的结点,也就是p的直接前驱,q指向的是
/ s的双亲结点,此时,应该看s的平衡因子,在会出现失去平衡的
/ 情况时,就要根据实际情况采用左平衡旋转或是右平衡旋转,让
/ 树恢复平衡,这点和插入操作时是相对应的。
/
/ 在中序遍历序列中找结点的直接前驱的方法是顺着结点的左孩子
/ 的右链域开始,一直到结点右孩子为空为止。
/---------------------------------------------------------*/
AvlNode *f=NULL;
AvlNode *p=NULL;
AvlNode *q=NULL;
AvlNode *s=NULL;
if(Search_Avl(T,num,f,p))
{
if(p->lchild && p->rchild) //左右子树均存在时
{
q=p;
s=p->lchild;
while(s->rchild)
{
q=s;
s=s->rchild;
}
p->data=s->data;
if(q!=p)
{
//q结点的右子树高度减少1
//所以平衡因子会+1
q->rchild=s->lchild;
switch(q->bf)
{
//删除前右子树高,现在就变成一样高
case RH:
q->bf=EH; break;
//删除前等高,现在就变成左子树比右子树高
case EH:
q->bf=LH; break;
//删除前左子树高,现在左子树又高了一,所以失去平衡
case LH:
q->bf=EH;
Left_Balance(q);
break;
}
}
else
{
//p的左子树的右子树为空时
//q结点也就是p结点,由于s的右子树为空
//所以q结点的左子树高度降低1
//平衡因子-1
q->lchild=s->lchild;
switch(q->bf)
{
case LH:
q->bf=EH;break;
case EH:
q->bf=RH;break;
case RH:
q->bf=EH;
Right_Balance(q);
break;
}
}
delete s;
cout<<"删除结点成功"<<endl;
return ;
}
else
{
if(!p->lchild)
{
q=p;
p=p->rchild;
}
else
{
q=p;
p=p->lchild;
}
if(!T)
{
T->bf=EH;
T=p;
}
else if(q==f->lchild)
{
f->lchild=p;
switch(f->bf)
{
case LH:
f->bf=EH; break;
case EH:
f->bf=RH; break;
case RH:
f->bf=EH;
Right_Balance(f);
break;
}
}
else
{
f->rchild=p;
switch(f->bf)
{
case RH:
f->bf=EH; break;
case EH:
f->bf=LH; break;
case LH:
f->bf=EH;
Left_Balance(f);
break;
}
}
delete q;
cout<<"删除结点成功"<<endl;
return;
}
}
else
{
cout<<"要删除的结点不存在"<<endl;
return;
}
}
InOrder_Traverse(AvlNode *T) //中序遍历
{
stack<AvlNode *> s;
AvlNode *p=T;
while(p || !s.empty())
{
if(p)
{
s.push(p);
p=p->lchild;
}
else
{
p=s.top();
s.pop();
cout<<p->data<<" ";
p=p->rchild;
}
}
}
void Level_Traverse(AvlNode *T) //层次遍历
{
queue<AvlNode *> q;
AvlNode *p=T;
q.push(p);
while(!q.empty())
{
p=q.front();
q.pop();
cout<<p->data<<" ";
if(p->lchild)
q.push(p->lchild);
if(p->rchild)
q.push(p->rchild);
}
}
};测试文件"main.cpp"#include"tree.h"
int main()
{
AVL_Tree tree;
AvlNode *root=NULL;
cout<<"____建立平衡二叉树____"<<endl;
tree.Create_AVl(root);
cout<<"中序遍历二叉树为:";
tree.InOrder_Traverse(root);
cout<<endl;
cout<<"层次遍历二叉树为:";
tree.Level_Traverse(root);
cout<<endl;
int num;
bool taller=false;
cout<<"输入你要插入的结点的值:";
cin>>num;
tree.Insert_Avl(root,num,taller);
cout<<"中序遍历二叉树为:";
tree.InOrder_Traverse(root);
cout<<endl;
AvlNode *f=NULL;
AvlNode *p=NULL;
cout<<"输入你要搜索的结点的值:";
cin>>num;
if(tree.Search_Avl(root,num,f,p))
{
cout<<"查找得到的结点值为:"<<tree.Get_data(p)<<"的地址为:"<<p<<endl;
if(f==NULL)
cout<<"因为结点"<<tree.Get_data(p)<<"是根结点,所以没有双亲结点"<<endl;
else
cout<<"该结点的双亲结点的值为:"<<tree.Get_data(f)<<endl;
}
else
cout<<"查找的结点不存在"<<endl;
cout<<"输入你要删除的结点的值:";
cin>>num;
tree.Delete_AVL(root,num);
cout<<"中序遍历二叉树为:";
tree.InOrder_Traverse(root);
cout<<endl;
return 0;
}测试结果
____建立平衡二叉树____ 输入平衡二叉树的元素,输入-1代表结束输入:16 3 7 11 9 26 18 14 15 -1 _____建树完成____ 中序遍历二叉树为:3 7 9 11 14 15 16 18 26 层次遍历二叉树为:11 7 18 3 9 15 26 14 16 输入你要插入的结点的值:20 中序遍历二叉树为:3 7 9 11 14 15 16 18 20 26 输入你要搜索的结点的值:20 查找得到的结点值为:20的地址为:00380BB0 该结点的双亲结点的值为:26 输入你要删除的结点的值:15 删除结点成功 中序遍历二叉树为:3 7 9 11 14 16 18 20 26 Press any key to continue
下面是四种旋转的示意图


先右后左的和先左后右的相对应的 所以不画了 下面再画一个建树的过程 就不画了 太费时间了画这个 刚好找到一个画好的 直接贴
因为下面图中它的计算平衡因子的方式是右子树高度减去左子树高度,所以和我上面的计算方法相反,不过不影响观看
建立含有元素 16 3 7 11 9 26 18 14 15 的平衡二叉树的过程如下所示:



相关文章推荐
- 平衡二叉树(AVL树)的基本操作
- 1773 Problem A 算法9-9~9-12:平衡二叉树的基本操作
- AVL树构建代码及其基本操作
- AVL---平衡二叉树的基本操作
- AVL树的基本操作
- Avl树的基本操作(c语言实现)
- 二叉树的基本操作(三)——AVL树的性质和插入操作
- AVL树的定义和基本操作
- 平衡二叉树的基本操作
- 平衡二叉树-AVL树的构建和操作
- AVL树的基本操作 HDU_4006 AVL树解法
- AVL树基本操作
- 二叉查找树和AVL树的基本操作(AVL树就是一颗特殊的二叉查找树。)
- 平衡二叉树(AVL树)一图一步骤代码实现左旋右旋,左右平衡操作
- 平衡二叉树AVL的基本操作之插入
- 标题:AVL树的基本操作例程(1)
- AVL树的基本操作之插入(递归与非递归编码)(2)
- AVL树的基本操作 C++
- 平衡二叉树AVL的基本操作之删除
- 平衡二叉树(AVL)的介绍及基本操作
