算法导论分而治之学习笔记
2011-04-27 21:43
253 查看
The divide-and-conquer design paradigm
1. Divide the problem (instance)
into subproblems.
2. Conquer the subproblems by
solving them recursively.
3. Combine subproblem solutions.
merge sort
1. Divide: Trivial.
2. Conquer: Recursively sort 2 subarrays.
3. Combine: Linear-time merge.

Master theorem (reprise)
T(n) = aT(n/b) + f (n)
CASE 1: f (n) = O(nlogba –ε)
⇒ T(n) = Θ(nlogba) .
CASE 2: f (n) =Θ(nlogba lgkn)
⇒ T(n) = Θ(nlogba lgk+1n) .
CASE 3: f (n) = Ω(nlogba +ε) and a f (n/b) ≤ c f (n)
⇒ T(n) = Θ( f (n)) .
Merge sort: a = 2, b = 2 ⇒ nlogba = n⇒ CASE 2 (k = 0) ⇒
T(n) = Θ(n lg n) .
Binary search
1. Divide: Check middle element.
2. Conquer: Recursively search 1 subarray.
3. Combine: Trivial.
Recurrence for binary search

nlogba = nlog21 = n0 = 1⇒ CASE 2 (k = 0)⇒
T(n) = Θ(lg n) .
Powering a number
Problem: Compute, where n ∈ N.
Naive algorithm: Θ(n).
Divide-and-conquer algorithm:
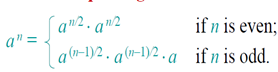
T(n) = T(n/2) + Θ(1) . T(n) = Θ(lg n) .
Fibonacci numbers
Recursive definition:

0 1 1 2 3 5 8 13 21 34 ….
Naive recursive algorithm: Ω()
(exponential time), where φ =(
)/2
is the golden ratio.
Computing Fibonacci numbers
Naive recursive squaring:
Fn = /
rounded to the nearest integer.
• Recursive squaring: Θ(lg n) time.
• This method is unreliable, since floating-point
arithmetic is prone to round-off errors.
Bottom-up
• Compute F0, F1, F2, …, Fn in order, forming
each number by summing the two previous.
• Running time: Θ(n).
Recursive squaring
Theorem:
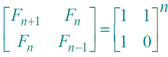
Algorithm: Recursive squaring.Time = Θ(lg n) .
Proof of theorem. (Induction on n.)
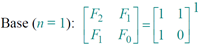
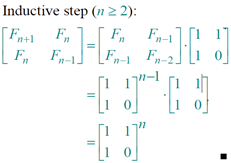
Matrix multiplication
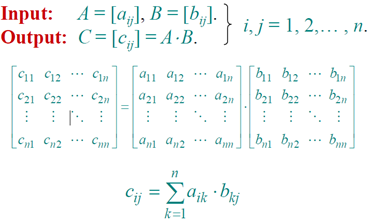
Standard algorithm
for i ← 1 to n
do for j ← 1 to n
do cij ← 0
for k ← 1 to n
do cij ← cij + aik⋅ bkj
Running time = Θ(n3)
Divide-and-conquer algorithm
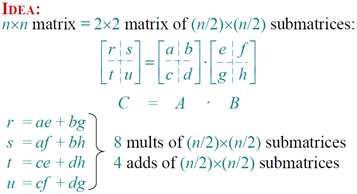
Analysis of D&C algorithm
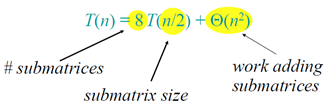
nlogba = nlog28 = n3 ⇒ CASE 1 ⇒ T(n) = Θ(n3).
No better than the ordinary algorithm.
Strassen's idea
• Multiply 2×2 matrices with only 7 recursive mults.
P1 = a ⋅ ( f – h)
P2 = (a + b) ⋅ h
P3 = (c + d) ⋅ e
P4 = d ⋅ (g – e)
P5 = (a + d) ⋅ (e + h)
P6 = (b – d) ⋅ (g + h)
P7 = (a – c) ⋅ (e + f )
r = P5 + P4 – P2 + P6
s = P1 + P2
t = P3 + P4
u = P5 + P1 – P3 – P7
7 mults, 18 adds/subs.
Note: No reliance on
commutativity of mult!
Strassen's algorithm
1. Divide: Partition A and B into
(n/2)×(n/2) submatrices. Form terms
to be multiplied using + and – .
2. Conquer: Perform 7 multiplications of
(n/2)×(n/2) submatrices recursively.
3. Combine: Form C using + and – on
(n/2)×(n/2) submatrices.
T(n) = 7 T(n/2) + Θ(n2)
Analysis of Strassen
T(n) = 7 T(n/2) + Θ(n2)
nlogba = nlog27 ≈ n2.81 ⇒ CASE 1 ⇒ T(n) = Θ(nlg 7).
The number 2.81 may not seem much smaller than
3, but because the difference is in the exponent, the
impact on running time is significant. In fact,
Strassen's algorithm beats the ordinary algorithm
on today's machines for n ≥ 30 or so.on today's machines for n ≥ 30 or so.
on today's machines for n ≥ 30 or so.
VLSI layout
Problem: Embed a complete binary tree
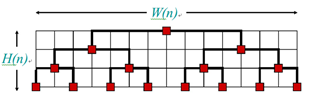
H(n) = H(n/2) + Θ(1) W(n) = 2 W(n/2) + Θ(1)
= Θ(lg n)= Θ(n)
with n leaves in a grid using minimal area.
Area = Θ(n lg n)

1. Divide the problem (instance)
into subproblems.
2. Conquer the subproblems by
solving them recursively.
3. Combine subproblem solutions.
merge sort
1. Divide: Trivial.
2. Conquer: Recursively sort 2 subarrays.
3. Combine: Linear-time merge.

Master theorem (reprise)
T(n) = aT(n/b) + f (n)
CASE 1: f (n) = O(nlogba –ε)
⇒ T(n) = Θ(nlogba) .
CASE 2: f (n) =Θ(nlogba lgkn)
⇒ T(n) = Θ(nlogba lgk+1n) .
CASE 3: f (n) = Ω(nlogba +ε) and a f (n/b) ≤ c f (n)
⇒ T(n) = Θ( f (n)) .
Merge sort: a = 2, b = 2 ⇒ nlogba = n⇒ CASE 2 (k = 0) ⇒
T(n) = Θ(n lg n) .
Binary search
1. Divide: Check middle element.
2. Conquer: Recursively search 1 subarray.
3. Combine: Trivial.
Recurrence for binary search

nlogba = nlog21 = n0 = 1⇒ CASE 2 (k = 0)⇒
T(n) = Θ(lg n) .
Powering a number
Problem: Compute, where n ∈ N.
Naive algorithm: Θ(n).
Divide-and-conquer algorithm:
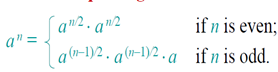
T(n) = T(n/2) + Θ(1) . T(n) = Θ(lg n) .
Fibonacci numbers
Recursive definition:

0 1 1 2 3 5 8 13 21 34 ….
Naive recursive algorithm: Ω()
(exponential time), where φ =(
)/2
is the golden ratio.
Computing Fibonacci numbers
Naive recursive squaring:
Fn = /
rounded to the nearest integer.
• Recursive squaring: Θ(lg n) time.
• This method is unreliable, since floating-point
arithmetic is prone to round-off errors.
Bottom-up
• Compute F0, F1, F2, …, Fn in order, forming
each number by summing the two previous.
• Running time: Θ(n).
Recursive squaring
Theorem:
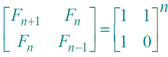
Algorithm: Recursive squaring.Time = Θ(lg n) .
Proof of theorem. (Induction on n.)
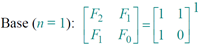
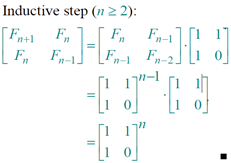
Matrix multiplication
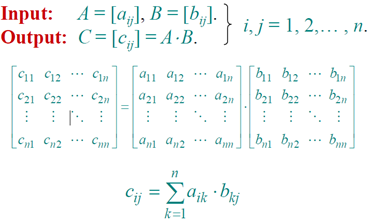
Standard algorithm
for i ← 1 to n
do for j ← 1 to n
do cij ← 0
for k ← 1 to n
do cij ← cij + aik⋅ bkj
Running time = Θ(n3)
Divide-and-conquer algorithm
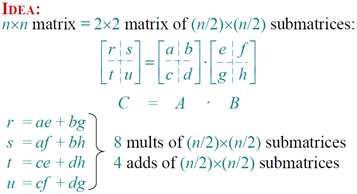
Analysis of D&C algorithm
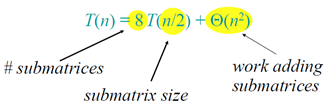
nlogba = nlog28 = n3 ⇒ CASE 1 ⇒ T(n) = Θ(n3).
No better than the ordinary algorithm.
Strassen's idea
• Multiply 2×2 matrices with only 7 recursive mults.
P1 = a ⋅ ( f – h)
P2 = (a + b) ⋅ h
P3 = (c + d) ⋅ e
P4 = d ⋅ (g – e)
P5 = (a + d) ⋅ (e + h)
P6 = (b – d) ⋅ (g + h)
P7 = (a – c) ⋅ (e + f )
r = P5 + P4 – P2 + P6
s = P1 + P2
t = P3 + P4
u = P5 + P1 – P3 – P7
7 mults, 18 adds/subs.
Note: No reliance on
commutativity of mult!
Strassen's algorithm
1. Divide: Partition A and B into
(n/2)×(n/2) submatrices. Form terms
to be multiplied using + and – .
2. Conquer: Perform 7 multiplications of
(n/2)×(n/2) submatrices recursively.
3. Combine: Form C using + and – on
(n/2)×(n/2) submatrices.
T(n) = 7 T(n/2) + Θ(n2)
Analysis of Strassen
T(n) = 7 T(n/2) + Θ(n2)
nlogba = nlog27 ≈ n2.81 ⇒ CASE 1 ⇒ T(n) = Θ(nlg 7).
The number 2.81 may not seem much smaller than
3, but because the difference is in the exponent, the
impact on running time is significant. In fact,
Strassen's algorithm beats the ordinary algorithm
on today's machines for n ≥ 30 or so.on today's machines for n ≥ 30 or so.
on today's machines for n ≥ 30 or so.
VLSI layout
Problem: Embed a complete binary tree

H(n) = H(n/2) + Θ(1) W(n) = 2 W(n/2) + Θ(1)
= Θ(lg n)= Θ(n)
with n leaves in a grid using minimal area.
Area = Θ(n lg n)

相关文章推荐
- 算法导论学习笔记之二--分而治之(divide-and-conquer approach)
- 算法导论学习笔记-1-4章
- 算法导论学习笔记(十二):动态规划(二):最长公共子序列(LCS)
- 算法导论学习笔记-第8章 线性时间排序
- 算法导论学习笔记----动态规划
- 算法导论学习笔记(四) 初稿
- 算法导论学习笔记(一)排序算法之分治排序
- 算法导论学习笔记——第1部分
- 算法导论学习笔记17_9_7
- 《算法导论》学习笔记--第十二章 二叉查找树
- 算法导论学习笔记(四):求X的N次方的二分实现
- 算法导论学习笔记-第十二章-二叉查找树
- 算法导论学习笔记之五--同时得到最大和最小值复杂度3(n/2)
- 算法导论学习笔记 6.5 优先队列
- 算法导论--学习笔记019
- 算法导论学习笔记——堆排序
- 算法导论学习笔记——第6章 堆排序
- 算法导论 学习笔记 第三章 函数的增长
- 算法导论学习笔记-5.1 雇佣问题
- 算法导论学习笔记(二):合并排序
