傅里叶分析中几个容易混淆的概念(转帖)
2010-05-06 13:46
381 查看
转自 http://blog.ednchina.com/yrwusignal/288071/message.aspx http://blog.csdn.net/dznlong/archive/2008/04/08/2261150.aspx
傅里叶分析可以说是信号处理最重要的基石之一。但傅里叶级数、傅里叶变换、离散时间傅里叶变换、离散傅里叶变换等几个有点像又有点不像的概念,不仅经常搞得初学者晕头转向,有时候让老手也有点糊涂。
根据原信号的不同类型,我们可以把傅立叶变换分为四种类别:
下图是四种原信号图例:

1、
傅里叶级数 --
周期连续信号的傅里叶分析
在高等数学中就已经知道,在满足一定的条件下,任何一个周期信号都可以分解为正弦信号的叠加。在高等数学中,这种分解就叫傅里叶级数。在信号处理学习的最初阶段,也是从这个概念出发,开始输入到信号处理的傅里叶世界。在信号处理中,周期连续信号的傅里叶分析称为傅里叶级数。此时,在傅里叶分析之前,信号是周期,连续的,在之后,结果是离散的。
定义
设

是

上以

为周期的函数,且

在

上绝对可积,称形如

的函数项级数为

的 Fourier级数
或三角级数
(

的 Fourier展开式),其中

,

,

记为

以

为周期的函数的Fourier级数
设

是以

为周期的函数,令

可以把

变换成以

为周期的t
的函数

。若

在

一可积,则

在

上可积,且

的Fourier级数展开式是

(1)
其中

(2)
因为

,所以

,于是由(1)(2)分别得

(3)
与

(4)
这里(4)式是以

为周期的函数

的Fourier系数,(3)式是

的Fourier级数。
2、
傅里叶变换 --
非周期连续信号的傅里叶分析
对于连续信号,如果信号不是周期的,其傅里叶分析结果又是如何呢?非周期信号可以等效为周期为无穷大的周期信号。于是,由傅里叶级数出发,利用极限的有关概念,可以推导出非周期信号的傅里叶分析结果,这就是傅里叶变换。再啰嗦一句,非周期连续信号的傅里叶分析称为傅里叶变换。在傅里叶分析之前,信号是非周期的,连续的,在之后,结果也是连续的。
对于非周期信号


前者是由信号的时间函数变换成频率函数,称为傅里叶正变换式,有时记为

或

后者是由信号的频率函数变换为时间函数,称为傅里叶反变换式。有时记为

或

如果上述变换中的自变量不用角频率

而用频率

,则由于

,可写为

频谱密度函数

是一复变函数,可以写为

式中

和

分别为

的模和相位,

和

分别为

的实部和虚部。
傅里叶反变换式也可写成

可见一个非周期信号

也可以分解成许多不同频率的正、余弦分量,也可以分解为t
的复变函数。若

是实函数,则

和

分别是ω的偶函数和奇函数,并且

3、
离散时间傅里叶变换 --
非周期离散信号的傅里叶分析
傅里叶级数和傅里叶变换都是针对连续信号而言的,那么对于数字信号而言,是否有对应的傅里叶分析呢?答案是肯定的,这就是离散时间傅里叶变换(
DTFT
)和离散傅里叶变换(
DFT
)。
对非周期离散信号的傅里叶分析称为离散时间傅里叶变换。在傅里叶分析之前,信号是非周期的,离散的,在之后,结果是连续的。
记连续时间信号f
(t
)
的采样为
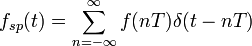
,
其傅里叶变换
为
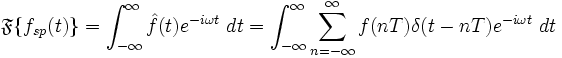
这就是采样序列f
(n
T
)
的DTFT:
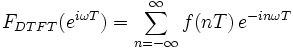
为方便起见,通常将采样间隔T归一化,则有
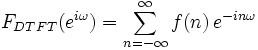
上式即为f
(n
)
的离散时间傅里叶变换
。
它的反变换
为:

考虑到DTFT的周期性(参见频
谱周期性
),它的逆变换实际上是以周期的连续函数作为输入,离散的谱作为输出,这正是傅里叶级数
的形式。
4、
离散傅里叶变换 --
周期离散信号的傅里叶分析
对周期离散信号的傅里叶分析称为离散傅里叶变换。在傅里叶分析之前,信号是周期的,离散的,在之后,结果是离散的。如果按照前面三种分析的命名,离散傅里叶变换叫离散傅里叶级数似乎更为妥当。但由于历史的原因,大家习惯把这种傅里叶分析称为离散傅里叶变换。当然,关于
DFT
是否隐含着信号周期性的问题,也有一些争论。有的认为进行
DFT
分析就意味着默认离散信号是周期的,有的则认为离散信号不一定要看成是周期的。此处采取默认离散信号周期性的说法,主要是基于如下理由:如果把
DFT
看做是对
DTFT
结果在频域的采样的话,那么根据信号系统的有关理论可知,频域的采样等效于时域的周期延拓,这样,离散信号自然变成周期的了。在实际分析中,将
DFT
看做是对
DTFT
结果在频域的采样是合乎情理的。
下面给出离散傅里叶变换的变换对:
对于N
点序列
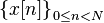
,
它的离散傅里叶变换(DFT)为
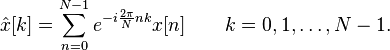
其中e
是自然对数
的底数
,i
是虚数单位
。通常以符号

表
示这一变换,即

离散傅里叶变换的逆变换(IDFT)为:
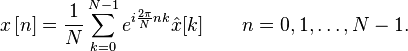
可以记为:

实际上,DFT和IDFT变换式中和式前面的归一化系数并不重要。在上面的定义中,DFT和IDFT前的系数分别为1
和1/N
。
有时会将这两个系数都改成

。
这上面的四个与傅里叶分析有关的概念,最重要的是
DFT
。因为前面三种分析都需要假定信号的时域及频域都是无限长的。从概念上讲,虽然
DFT
也需要时域频域无限长,但由于时域频域都是周期的,因此只需要一个周期的信息即可。另外,由于计算机等数字设备只能
处理数字信号,也即是要求无论是时域还是频域,都要是离散的。因此,
DFT
在实践中占有最重要的地位。傅里叶级数,傅里叶变换,离散时间傅里叶变换
这三个概念则更多的用于理论分析中。

傅里叶分析可以说是信号处理最重要的基石之一。但傅里叶级数、傅里叶变换、离散时间傅里叶变换、离散傅里叶变换等几个有点像又有点不像的概念,不仅经常搞得初学者晕头转向,有时候让老手也有点糊涂。
根据原信号的不同类型,我们可以把傅立叶变换分为四种类别:
| 1 | 非周期性连续信号 | 傅立叶变换(Fourier Transform) |
| 2 | 周期性连续信号 | 傅立叶级数(Fourier Series) |
| 3 | 非周期性离散信号 | 离散时域傅立叶变换(Discrete Time Fourier Transform) |
| 4 | 周期性离散信号 | 离散傅立叶变换(Discrete Fourier Transform) |

1、
傅里叶级数 --
周期连续信号的傅里叶分析
在高等数学中就已经知道,在满足一定的条件下,任何一个周期信号都可以分解为正弦信号的叠加。在高等数学中,这种分解就叫傅里叶级数。在信号处理学习的最初阶段,也是从这个概念出发,开始输入到信号处理的傅里叶世界。在信号处理中,周期连续信号的傅里叶分析称为傅里叶级数。此时,在傅里叶分析之前,信号是周期,连续的,在之后,结果是离散的。
定义
设

是

上以

为周期的函数,且

在

上绝对可积,称形如

的函数项级数为

的 Fourier级数
或三角级数
(

的 Fourier展开式),其中

,

,

记为

以

为周期的函数的Fourier级数
设

是以

为周期的函数,令

可以把

变换成以

为周期的t
的函数

。若

在

一可积,则

在

上可积,且

的Fourier级数展开式是

(1)
其中

(2)
因为

,所以

,于是由(1)(2)分别得

(3)
与

(4)
这里(4)式是以

为周期的函数

的Fourier系数,(3)式是

的Fourier级数。
2、
傅里叶变换 --
非周期连续信号的傅里叶分析
对于连续信号,如果信号不是周期的,其傅里叶分析结果又是如何呢?非周期信号可以等效为周期为无穷大的周期信号。于是,由傅里叶级数出发,利用极限的有关概念,可以推导出非周期信号的傅里叶分析结果,这就是傅里叶变换。再啰嗦一句,非周期连续信号的傅里叶分析称为傅里叶变换。在傅里叶分析之前,信号是非周期的,连续的,在之后,结果也是连续的。
对于非周期信号


前者是由信号的时间函数变换成频率函数,称为傅里叶正变换式,有时记为

或

后者是由信号的频率函数变换为时间函数,称为傅里叶反变换式。有时记为

或

如果上述变换中的自变量不用角频率

而用频率

,则由于

,可写为

频谱密度函数

是一复变函数,可以写为

式中

和

分别为

的模和相位,

和

分别为

的实部和虚部。
傅里叶反变换式也可写成

可见一个非周期信号

也可以分解成许多不同频率的正、余弦分量,也可以分解为t
的复变函数。若

是实函数,则

和

分别是ω的偶函数和奇函数,并且

3、
离散时间傅里叶变换 --
非周期离散信号的傅里叶分析
傅里叶级数和傅里叶变换都是针对连续信号而言的,那么对于数字信号而言,是否有对应的傅里叶分析呢?答案是肯定的,这就是离散时间傅里叶变换(
DTFT
)和离散傅里叶变换(
DFT
)。
对非周期离散信号的傅里叶分析称为离散时间傅里叶变换。在傅里叶分析之前,信号是非周期的,离散的,在之后,结果是连续的。
记连续时间信号f
(t
)
的采样为
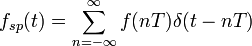
,
其傅里叶变换
为
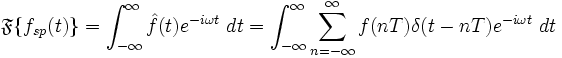
这就是采样序列f
(n
T
)
的DTFT:
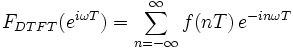
为方便起见,通常将采样间隔T归一化,则有
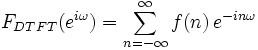
上式即为f
(n
)
的离散时间傅里叶变换
。
它的反变换
为:

考虑到DTFT的周期性(参见频
谱周期性
),它的逆变换实际上是以周期的连续函数作为输入,离散的谱作为输出,这正是傅里叶级数
的形式。
4、
离散傅里叶变换 --
周期离散信号的傅里叶分析
对周期离散信号的傅里叶分析称为离散傅里叶变换。在傅里叶分析之前,信号是周期的,离散的,在之后,结果是离散的。如果按照前面三种分析的命名,离散傅里叶变换叫离散傅里叶级数似乎更为妥当。但由于历史的原因,大家习惯把这种傅里叶分析称为离散傅里叶变换。当然,关于
DFT
是否隐含着信号周期性的问题,也有一些争论。有的认为进行
DFT
分析就意味着默认离散信号是周期的,有的则认为离散信号不一定要看成是周期的。此处采取默认离散信号周期性的说法,主要是基于如下理由:如果把
DFT
看做是对
DTFT
结果在频域的采样的话,那么根据信号系统的有关理论可知,频域的采样等效于时域的周期延拓,这样,离散信号自然变成周期的了。在实际分析中,将
DFT
看做是对
DTFT
结果在频域的采样是合乎情理的。
下面给出离散傅里叶变换的变换对:
对于N
点序列
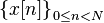
,
它的离散傅里叶变换(DFT)为
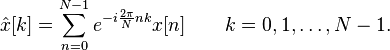
其中e
是自然对数
的底数
,i
是虚数单位
。通常以符号

表
示这一变换,即

离散傅里叶变换的逆变换(IDFT)为:
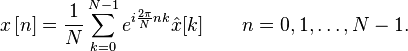
可以记为:

实际上,DFT和IDFT变换式中和式前面的归一化系数并不重要。在上面的定义中,DFT和IDFT前的系数分别为1
和1/N
。
有时会将这两个系数都改成

。
这上面的四个与傅里叶分析有关的概念,最重要的是
DFT
。因为前面三种分析都需要假定信号的时域及频域都是无限长的。从概念上讲,虽然
DFT
也需要时域频域无限长,但由于时域频域都是周期的,因此只需要一个周期的信息即可。另外,由于计算机等数字设备只能
处理数字信号,也即是要求无论是时域还是频域,都要是离散的。因此,
DFT
在实践中占有最重要的地位。傅里叶级数,傅里叶变换,离散时间傅里叶变换
这三个概念则更多的用于理论分析中。

相关文章推荐
- 傅里叶分析中几个容易混淆的概念
- 傅里叶分析中几个容易混淆的概念
- WCDMA缩略语 & 几个容易混淆的概念 & 关于掉话原因分析
- XML数据库中几个容易混淆的概念
- js中几个容易混淆的概念
- XML数据库中几个容易混淆的概念
- Python中几个容易混淆的概念:列表、元组、字典、集合
- 数据库学习中几个容易混淆的概念
- 【Web Tricks 10】web编程中几个容易混淆的函数(概念)
- easyrec推荐系统学习过程中容易混淆的几个概念
- Java中几个容易混淆的相似概念和关键字的区别与用法梳理
- XML数据库中几个容易混淆的概念
- 介绍几个XML数据库中容易混淆的概念
- XML数据库中几个容易混淆的概念
- javascript中几个容易混淆的概念总结
- UML 类图容易混淆的几个概念
- 嵌入式实时操作系统几个比较容易混淆的概念
- 黑马程序员-Java容易混淆的几个概念
- XML数据库中几个容易混淆的概念
- 软件测试中比较容易混淆的几个概念
