绪论和第一章集合论初步
2010-01-24 09:03
274 查看
看到电驴上有北师大郇中丹老师的数学分析视频,刚好最近比较空闲,想再看看数分,就稍微整理了下笔记。
不要热衷于罗列众多的其他教科书,罗列各种处理方式,搜寻各种习题的他人解法
集合论初步
1.集合论和数学的严密性
什么是数学的严密性或逻辑性
数学的严密性在于:
交代清楚要讨论的问题或对象
交代清楚定义、证明或叙述中要用到的概念和关系(叫做原始概念和原始关系)
只利用这些概念和关系,遵循逻辑规则完成对问题的证明、叙述或模型的建立
数学的严格性是历史的,其逻辑性是在科学和数学的发展中不断深化的
数学如何实现其严密性
皮亚诺公理系统(自然数不包含0,但是现在欧美系统都是自然数包含0)
基本前提:自然数集合存在,在上面可以定义相等
公理1.1是自然数
公理2.每个自然数可以定义唯一的后邻
公理3.任何后邻都不会是1
公理4.若两数的后邻相等,则两数相等
公理5.归纳法成立
ZFC公理集合论系统
原始概念:集合
原始关系:属于
公理:外延公理(相等)、空集公理、配对公理、并集公理、幂集公理、无穷公理(归纳法)、公式Φ的替换公理、正则公理、选择公理
现代数学方法:集合论+公理化
集合是定义任何数学对象的原始概念。数学上说,任何数学概念都是用集合定义的,简单地说,任何数学对象都是其中类型的集合
数学系统都以公理化的形式和精神来陈述的探索的。
数学严格性与实用性的妥协
在现实的数学学习和从事数学研究的过程中,人们并非真的能够和没有意义抽象符号打交道,而是用人们能够赋予实际意义的符号处理问题。因此不少时候人们试图去给集合下“定义”,实际上是让初学者理解其实际含义。
另一方面数学中所发现的悖论在不时地提醒人们这种直观能够走多远。
2.集合及其运算
集合(直观描述)
具有某种属性的对象总体(通常用大写字母表示,如A、B等),这些对象称为其元素或点(通常用小写字母表示,如x、y等)
X是A的元素记为:
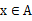
(读作x属于A)
X不是A的元素记为:
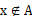
(读作x不属于A)
集合的基本特性是:对于给定的集合A,任何对象x,
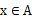
与
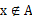
中有且只有一个成立
集合相等和子集合
集合相等:如果两个集合A和B有同样的元素组成,就说集合A和B相等,几座A=B或B=A
子集合:如果集合B的元素都是集合A的元素,B叫做A的子集合(简称子集),记作
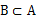
(读作B包含于A),或
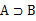
(读作A包含B)
命题:A=B当且仅当
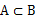
且
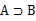
子集的表示方式和全集
设A是一个集合,其子集B通常用下面的形式表示:
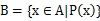
,其中P(x)表示x在B中所要满足的条件
空集:不含任何元素的集合叫做空集。用符号Φ来表示。空集是任何集合的子集:
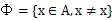
在数学的讨论中,常涉及到的是某个固定集合的子集,例如,实数的子集。这个固定集合叫做全集,一般用E表示
常用数学符号和常用集合记号
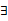
:表示存在,读作“存在”(there exist(s))
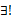
:表示存在唯一的,读作“存在唯一的”(there exists unique)
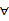
:表示对于所有的或任意的,读作“对于任意的”或“对于所有的”(for all)
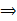
:表示能够推得,读作“蕴含”(imply)
自然数N,整数Z,有理数Q,实数R(
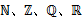
)
集合的并
集合A和B的并是自A或B的所有元素组成的集合,记为
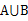
,也就是
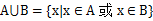
集合并运算的性质
交换律
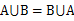
集合律
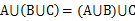
集合族
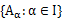
的并
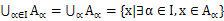
I为自然数时的记法
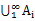
集合的交
集合的差运算和余(补)运算
集合运算的性质
3.笛卡尔积
4.映射和函数
5.集合的势
不要热衷于罗列众多的其他教科书,罗列各种处理方式,搜寻各种习题的他人解法
集合论初步
1.集合论和数学的严密性
什么是数学的严密性或逻辑性
数学的严密性在于:
交代清楚要讨论的问题或对象
交代清楚定义、证明或叙述中要用到的概念和关系(叫做原始概念和原始关系)
只利用这些概念和关系,遵循逻辑规则完成对问题的证明、叙述或模型的建立
数学的严格性是历史的,其逻辑性是在科学和数学的发展中不断深化的
数学如何实现其严密性
皮亚诺公理系统(自然数不包含0,但是现在欧美系统都是自然数包含0)
基本前提:自然数集合存在,在上面可以定义相等
公理1.1是自然数
公理2.每个自然数可以定义唯一的后邻
公理3.任何后邻都不会是1
公理4.若两数的后邻相等,则两数相等
公理5.归纳法成立
ZFC公理集合论系统
原始概念:集合
原始关系:属于
公理:外延公理(相等)、空集公理、配对公理、并集公理、幂集公理、无穷公理(归纳法)、公式Φ的替换公理、正则公理、选择公理
现代数学方法:集合论+公理化
集合是定义任何数学对象的原始概念。数学上说,任何数学概念都是用集合定义的,简单地说,任何数学对象都是其中类型的集合
数学系统都以公理化的形式和精神来陈述的探索的。
数学严格性与实用性的妥协
在现实的数学学习和从事数学研究的过程中,人们并非真的能够和没有意义抽象符号打交道,而是用人们能够赋予实际意义的符号处理问题。因此不少时候人们试图去给集合下“定义”,实际上是让初学者理解其实际含义。
另一方面数学中所发现的悖论在不时地提醒人们这种直观能够走多远。
2.集合及其运算
集合(直观描述)
具有某种属性的对象总体(通常用大写字母表示,如A、B等),这些对象称为其元素或点(通常用小写字母表示,如x、y等)
X是A的元素记为:
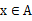
(读作x属于A)
X不是A的元素记为:
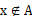
(读作x不属于A)
集合的基本特性是:对于给定的集合A,任何对象x,
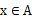
与
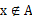
中有且只有一个成立
集合相等和子集合
集合相等:如果两个集合A和B有同样的元素组成,就说集合A和B相等,几座A=B或B=A
子集合:如果集合B的元素都是集合A的元素,B叫做A的子集合(简称子集),记作
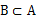
(读作B包含于A),或
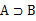
(读作A包含B)
命题:A=B当且仅当
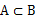
且
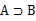
子集的表示方式和全集
设A是一个集合,其子集B通常用下面的形式表示:
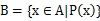
,其中P(x)表示x在B中所要满足的条件
空集:不含任何元素的集合叫做空集。用符号Φ来表示。空集是任何集合的子集:
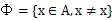
在数学的讨论中,常涉及到的是某个固定集合的子集,例如,实数的子集。这个固定集合叫做全集,一般用E表示
常用数学符号和常用集合记号
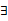
:表示存在,读作“存在”(there exist(s))
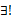
:表示存在唯一的,读作“存在唯一的”(there exists unique)
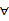
:表示对于所有的或任意的,读作“对于任意的”或“对于所有的”(for all)
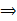
:表示能够推得,读作“蕴含”(imply)
自然数N,整数Z,有理数Q,实数R(
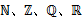
)
集合的并
集合A和B的并是自A或B的所有元素组成的集合,记为
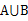
,也就是
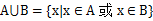
集合并运算的性质
交换律
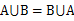
集合律
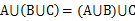
集合族
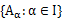
的并
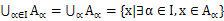
I为自然数时的记法
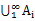
集合的交
集合的差运算和余(补)运算
集合运算的性质
3.笛卡尔积
4.映射和函数
5.集合的势
相关文章推荐
- 数据结构终结版总结----第一章 绪论
- [机器学习 - 周志华] - 第一章 绪论
- 数据结构(c++版)(第2版)第一章:绪论的知识点总结图,制作者:信管1134-28
- 数据结构 第一章绪论
- 第一章 绪论 --基于mkCDrec的核心网网络运维系统的备份和恢复的研究与实现
- 第一章绪论
- 数据结构 第一章绪论 学习笔记
- 第一章绪论的思维导论图
- 第一章 绪论思维导图
- 数据结构 第一章 绪论 思维导图
- 数据结构:第一章绪论总结
- 第一章 绪论
- 第一章 绪论 总结
- 第一章(绪论)
- 数据结构 第一章绪论 思维导图
- 胡说八道侃计算机——第一章绪论
- 第一章 JAVA初步
- Spring参考手册-第一章 绪论
- 谭浩强版C++课本实例 第一章 c++的初步认识
- 《机器学习》周志华学习笔记——第一章 绪论
