DCE和DTE的理解
2009-09-12 17:41
176 查看
算法定义:解决特定问题的求解步骤的描述,在计算机中表现为指令的有限序列,每条指令表示一个或多个操作。
算法的特性:
输入输出:输入0或多,输出1或多
有穷:执行有限的步骤,可以自动结束,可接受时间
可行:每一步都能通过执行有限次数完成
确定:只有一条执行路径,不会有二义性
算法的设计要求:
正确:
健壮:输入不合法不会产生异常和错误
可读:
时间空间效率高
算法效率度量方法
事后统计:有缺陷,依赖于系统软硬件
事前估计:抛开软硬件,主要依赖于算法设计和问题规模
算法的渐进增长:
给定f(n)和g(n),如果存在整数N,当所有n>N,f(n)总是比g(n)大,则f(n)的渐 进增长快于g(n)
忽略加法常数、忽略最高次项的项数、忽略所有非最高次项
算法的时间复杂度
首先计算T(n),它是确切的执行次数。
接着由T(n)推到O(f(n)),方法是用常数1代替所有常数项,只保留最高项,如果 最高项存在且不是1,去除最高项的项数
举例
复杂度排行
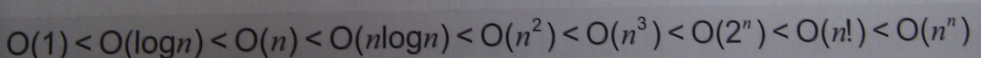
本文出自 “狂战” 博客,请务必保留此出处http://fanaticssk.blog.51cto.com/4148464/832369
算法的特性:
输入输出:输入0或多,输出1或多
有穷:执行有限的步骤,可以自动结束,可接受时间
可行:每一步都能通过执行有限次数完成
确定:只有一条执行路径,不会有二义性
算法的设计要求:
正确:
健壮:输入不合法不会产生异常和错误
可读:
时间空间效率高
算法效率度量方法
事后统计:有缺陷,依赖于系统软硬件
事前估计:抛开软硬件,主要依赖于算法设计和问题规模
算法的渐进增长:
给定f(n)和g(n),如果存在整数N,当所有n>N,f(n)总是比g(n)大,则f(n)的渐 进增长快于g(n)
忽略加法常数、忽略最高次项的项数、忽略所有非最高次项
算法的时间复杂度
首先计算T(n),它是确切的执行次数。
接着由T(n)推到O(f(n)),方法是用常数1代替所有常数项,只保留最高项,如果 最高项存在且不是1,去除最高项的项数
举例
//常数阶
int sum = 0,n = 100;
sum = (n+1) * n /2;//只执行了一次,此时T(n)=1=O(f(1))
printf("%d",sum);
//线性阶
int i;
for(i=0;i<n;i++){
}//T(n)=n= O(f(n))
//对数阶
int count = 1;
while(count<n){
count = count * 2;
}//问题就是这个循环执行多少次?假设执行x次,则有count=2的x次方,且count<n,所以有2的x次方<n
//结果就是T(n)=log以2为底n=O(f(logn)) ,在这次计算中我们将n当做已知,解方程即可
//平方阶
int i,j;
for(i=0;i<n;i++){
for(j=0;j<n;j++){//T(n)=O(f(n2次方))
}
}
int i,j;
for(i=0;i<n;i++){
for(j=0;j<m;j++){//T(n)=O(f(n*m))
}
}
int i,j;
for(i=0;i<n;i++){
for(j=i;j<n;j++){//当i=0,内循环n次,i=1时,内循环n-1次......n+(n-1)+(n-2).....+1+0=1/2(n平方)+1/2(n)=O(f(n平方))
}
}
n++;//1
function(n);//n
int i,j;
for(i=0;i<n;i++){//n平方
function(i);
}
for(i=0;i<n;i++){//(n(n+1))/2
for(j=i;j<n;j++){
}//O(f(n平方))
}复杂度排行
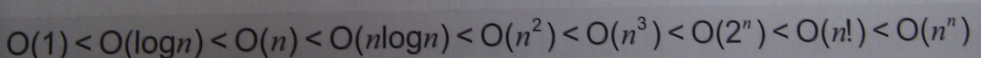
本文出自 “狂战” 博客,请务必保留此出处http://fanaticssk.blog.51cto.com/4148464/832369
