GPU求解粘性不可压流体
2007-04-05 19:28
267 查看
随着科学计算可视化、医疗图像、虚拟现实等学科的发展和娱乐产业的推动,高性能计算往往伴随着计算机图形应用。目前图形处理器的浮点计算性能已超过同等级CPU的性能。一些的研究者把非图形领域的计算从CPU 转移到GPU上,称为图形处理器的通用计算即GPGPU(General Purpose Computation on GPUs)
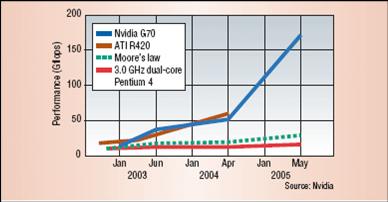
图-9 GPU和CPU浮点运算性能比较
2000年Hopf 在GPU上实现小波变换,2001年Larsen利用多纹理技术做矩阵运算,2002年Harris在GPU上用细胞自动机(CA)仿真各种物理现象,Purcell加速光线跟踪算法。2003年是GPGPU领域具有里程碑意义的一年,Kruger实现了线性代数操作,Li实现了Lattice Boltzmann的流体仿真,Lefohn实现了Level Set方法等一大批成果。2004年,Govindaraju在数据库领域应用取得进展。商业领域,Apple推出支持GPU的视频工具,2005年10月ATi和物理引擎厂商Havok宣布合作开发基于GPGPU的物理计算API。这期间,GPGPU应用领域越来越广,也越来越深入;图形标准API也相应推出一些新特性,提升图形应用的同时兼顾通用计算;GPU硬件厂商也通过这些研究发现不足,从而改进自己的图形处理器。
在GPU上实现流体的计算与仿真是GPGPU在科学计算中应用研究的热点。由于GPU特殊的体系和编程模型,在图形处理器上实现高效的数值仿真需要数值方法具有以下特点:
1)简洁的数据结构。GPU通用计算以纹理作为输入数据,片元程序作为计算核。复杂的数据结构需要在片元程序中计算纹理偏移,保留较多的中间变量,导致计算核计算效率下降。
2)精简的计算步骤。采用多遍绘制需要把输出的数据保存至纹理,以供下一个计算核取用。多遍绘制是个耗时的过程,所以在计算中要尽量减少多遍绘制次数。
3)统一的计算表达。由于GPU采用SIMD的并行计算方式,统一的数据表达有助于减少片元程序中条件和分支语句的使用,提高计算核的效率。
代表性的相关研究工作如下:
[1]Krüger J, Westermann R. Linear Algebra Operators for GPU Implementation of Numerical Algorithms [J]. ACM Trans. on Graphics,2003,22(3):908-916
[2]Harris M J. Fast Fluid Dynamics Simulation on the GPU [A].Fernando R.GPU Gems: Programming Techniques, Tips, and Tricks for Real-Time Graphics[M]. America:Addison-Wesley,2004. pp.637-665
[3]Wu EH, Liu YQ, Liu XH. An Improved Study of Real-time Fluid Simulation on GPU. Journal of Computer Animation & Virtual World (invited paper ofCASA2004), 2004,15(3-4):139~146
[4]Liu Y Q, Liu X H, Wu E H. Real-Time 3D Fluid Simulation on GPU with Complex Obstacles [C]. In Proc. of Pacific Graphics 2004, IEEE Computer Society, Oct. 2004, pp.247-256
[5]Scheidegger C E, Comba J L D, Cunha R D. Navier-Stokes on Programmable Graphics Hardware using SMAC [C] Proceedings of the XVII Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI’04),2004,pp.300-307
[6]Li W, Fan Z, Wei XM, Kaufman A. GPU-Based Flow Simulation With Complex Boundaries. Technical Report, Computer Science Department, SUNY at Stony Brook, 2003.
除了[6]中使用Lattice Boltzmann方法外,其余的方法使用的都是经典的计算流体力学数值方法,J. Stam的Stable Fluid方法。该计算方法在图形仿真领域被广泛使用,但是由于数值耗散过大,该方法仅能满足视觉上的效果而不具工程上的指导意义。[5]所采用的MAC方法由于采用显式的方程解法,受到数值稳定性问题的困扰,在应用中受到限制。所以我们希望能够找到一中折中的方法:它在保证求解速度的同时能够相对提高仿真精度。
在计算流体力学(CFD)对非定常不可压流动方程的数值模拟中,通常将速度和压力解耦, 分别求解速度和压力, 常见的有SIMPLE方法和投影方法。SIMPLE 方法在计算非定常流动时, 需要进行很多次内迭代, 计算效率较低, 而投影方法通过预测和校正两步, 就得到了新时刻的速度和压力, 因而具有较高的计算效率。综合GPU计算的特点和已有的工作,我们选取文献[7]Ye T, Mittal R, Udaykumar H S. An Accurate Cartesian Grid Method for Viscous Incompressible Flows with Complex Immersed Boundaries [J]. Journal of Computational Physics,1999,156,209-240的计算方法,在笛卡儿网格下用投影法做不可压流体的数值仿真。为了能理解这篇文献,我们先介绍一些基础的概念
1. Navier-Stokes方程和有限体元离散方法
1822年Navier建立了粘性流体的基本运动方程,后来Stokes完善了该方程,称作Navier-Stokes 方程,是计算流体力学的基础。考虑没有外力作用的粘性不可压流体的Navier-Stokes方程,其控制方程的无量纲形式为:
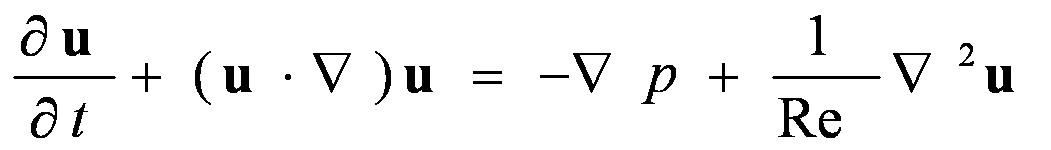
(1)
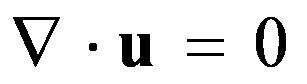
(2)
该方程组由对流场中某一确定的空间区域的受力分析得到,该空间区域称作控制体。控制体的边界称作控制面。其中方程(2-1)由控制体的动量守恒得到,在Navier-Stokes方程组中称为动量方程。方程(2)反映了控制体的质量守恒性质,称作连续性方程。方程中u为速度向量,p为压力,Re为反映流体粘性属性的雷诺系数。在方程(1)中,左边第一项称为时间倒数项,第二项为对流项;右边第一项称为压力梯度项,第二项为粘性耗散项。
在方程(1)两端对控制体进行积分,应用高斯公式后,原微分方程变为如下的积分形式:
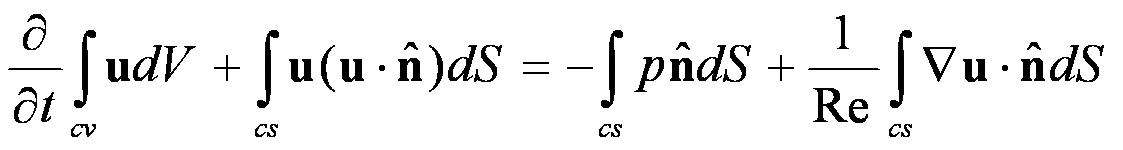
(3)
其中cv代表控制体,cs代表控制面。流场空间由控制面分成有限个的控制体单元,利用高斯公式把变量在控制体内的积分变成在控制面上的积分,该方法称为有限体元离散方法。下图-10所示为流体的变量在2维非交错笛卡儿网格上有限体元离散方法。
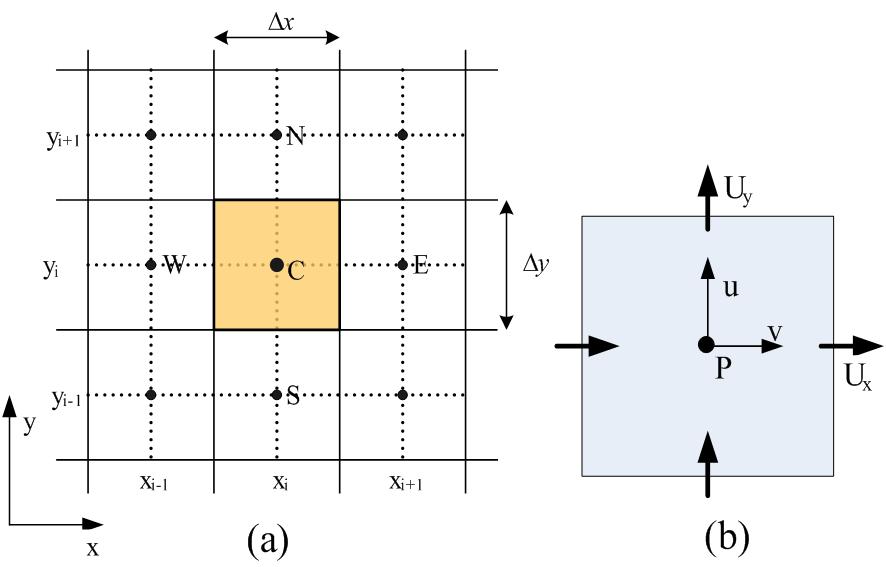
图-10
2.Helmholtz-Hodge分解和投影法
Chorin最早提出投影方法(Projection Method),是一种将速度和压力解耦来求解的不可压粘性方程的数值方法。该方法是分为预测-校正的两步:第1步,不考虑不可压条件,在一个估计的压力下求解动量方程得到所谓中间速度场,第2步,将中间速度场进行Helmholtz-Hodge分解,这个过程称为速度场的"投影",由此可以得到满足连续方程的速度场,并对压力场进行修正。该方法又称为分步法(Fractional-Step Method)。
Helmholtz-Hodge分解理论指出,任何一个矢量场w可唯一的分解为一个散度为零的矢量场u和一个标量场p的梯度之和,如(4)所示,其中将(2)代入方程 。所以这个散度为零的矢量场可以如(5)表达。
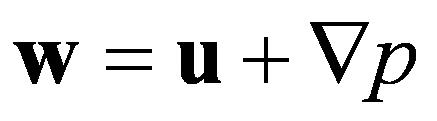
(4)
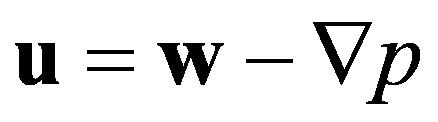
(5)
如果对(4)方程两边求散度,得到(6)的表达,该表达式称为压力泊松方程。
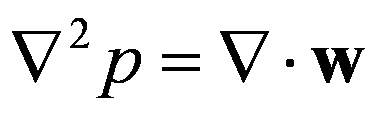
(6)
投影法的分步解法对Navier-Stokes方程采用Helmholtz-Hodge分解,可以将压力项从动量方程中移出,先求解中间速度场w,然后用(6)求解压力场p,最后用(5)对中间速度场进行压力校正,求出最终速度场u。
3.笛卡儿网格下投影法求解非定常流
把上述的方法应用于有限体元离散的形式,可以得到我们使用的方法。对方程(3)的对流项采用Adams-Bashforth 的二阶格式处理,对耗散项采用隐式的Crank-Nicolson方式离散。采用上述的离散方式消除了对粘性稳定性的限制。没有压力梯度项的方程(3),写成半隐式的离散形式如(7)所示:
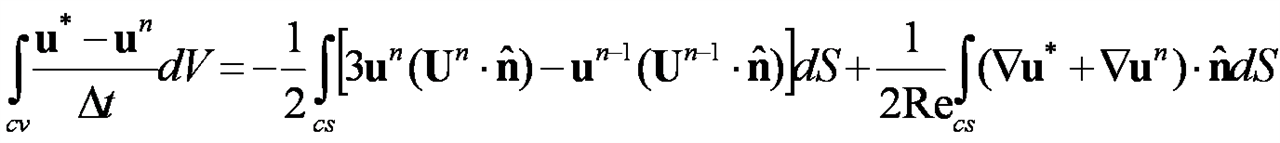
(7)
其中u*表示中间速度场,定义在每个有限体的中心位置,U为控制面速度,定义在每个控制面的中心位置。上标n代表时间步, 表示垂直于边界的外法向量。采用非交错网格如图-10(a)所示,每个有限体元变量位置的定义如图-10(b)所示。方程(7)的中间速度场的边界条件设为物理边界条件,即边界位置的中间速度等于边界位置的下一时刻的实际速度。重写投影方程和连续性方程,可以积分形式下的泊松方程(8),
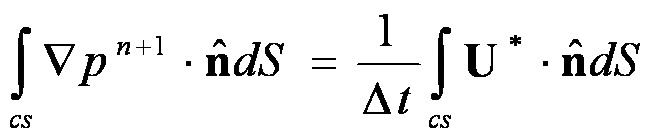
(8)
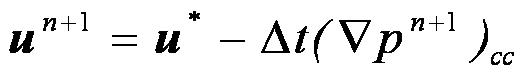
(9)
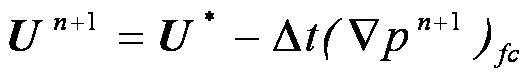
(10)
其中U*为中间速度场的控制面中心的速度,由插值相邻的中间速度得到。该泊松方程的压力边界条件为统一的Neumann边界条件,即边界上压力梯度在外法向上为0。经过(7)和(8)计算中间速度场和压力场之后,最终的速度场由方程(9)(10)得到,其中cc 和fc表示在控制体中心和控制面上求压力的梯度。最终速度的边界条件为 。
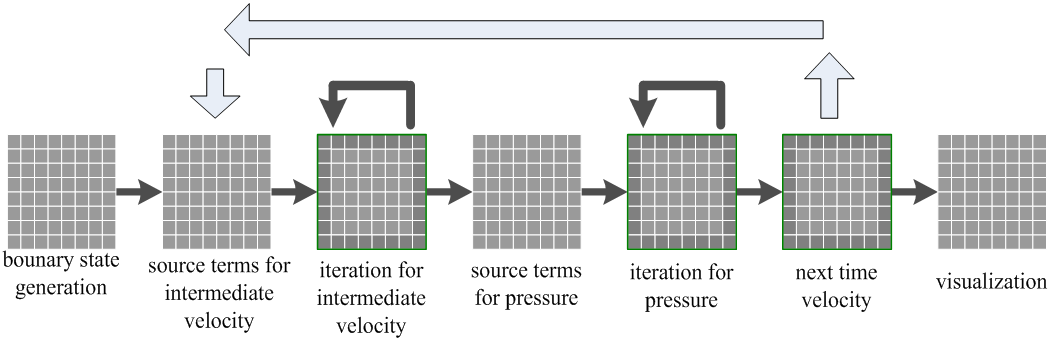
当下一时刻的各个场的值都知道后,可以重新开始新一轮计算,在时间上不断推进各个变量。综合以上计算,总的计算过程为以下3步骤:
1)计算迭代中间速度场,方程(7)
2)由中间速度场计算迭代压力场,方程(8)
3)由压力场计算下一时刻速度场,方程(9)(10)
整个操作过程如图-11所示,我们在NVIDIA GeForce 5700 GPU 128MB显存, 128bits带宽,驱动程序版本为66.72;AMD 650MHz CPU 192MB内存,AGP 4X上实现所有的算法。为了使整个计算在32位浮点精度上运行,需要综合使用OPENGL扩展 。GL_NV_texture_rectangle和NV_float_buffer配合使用可得到浮点纹理。WGL_ARB_pbuffer和NV_float_buffer配合使用会得到浮点的pbuffer。WGL_ARB_pbuffer、NV_float_buffer、GL_NV_texture_rectangle、NV_render_texture_rectangle和WGL_ARB_render_texture使用会获得浮点数的绘制到纹理操作。
对 GPU 通用计算流程和OpenGL性能进行测试,我们假定一个多遍绘制的通用计算应用需要如下一些步骤:
1) 初始化数据:在主存中初始化数据空间,给数组赋初值。
2)
初始化第1遍绘制的纹理:把主存中数据传到显存中,用第1步初始化的数组给二维纹理赋初值。
3) 使pbuffer有效,绑定当前纹理
4)
绑定片元程序
5)
并行程序执行:绘制矩形,设纹理坐标,图形管线执行片断程序
6)
获取中间数据:把pbuffer中的数据传递到纹理中,为下一遍绘制作准备。拷贝到纹理,重复5~7步,多遍计算。
7)
返回数据到主存:把存在显存pbuffer中的结果返回到主存中。该步骤可选方法有:7.1)选用pixel_buffer_object,启用DMA传输;7.2)直接使用glReadPixels。
8) 数据后期处理
在Windows XP操作系统下测试整个计算过程,采用同一个简单的线性插值片元程序,分别对128×128、256×256、512×512这3组数据计算进行测试,结果如下表。
通用计算总过程测试表
从该表中可以看出,图形操作显存和主存之间传递数据是耗时的过程,包括2和7.2步骤。从第4步的测试可以看出对于同样的片元程序,它的计算耗时和数据规模成正比,即数据规模每增长4倍,耗时也增长4倍。所以,优化GPU 的通用计算应该尽量减少显存和主存之间的数据传递。

图-9 GPU和CPU浮点运算性能比较
2000年Hopf 在GPU上实现小波变换,2001年Larsen利用多纹理技术做矩阵运算,2002年Harris在GPU上用细胞自动机(CA)仿真各种物理现象,Purcell加速光线跟踪算法。2003年是GPGPU领域具有里程碑意义的一年,Kruger实现了线性代数操作,Li实现了Lattice Boltzmann的流体仿真,Lefohn实现了Level Set方法等一大批成果。2004年,Govindaraju在数据库领域应用取得进展。商业领域,Apple推出支持GPU的视频工具,2005年10月ATi和物理引擎厂商Havok宣布合作开发基于GPGPU的物理计算API。这期间,GPGPU应用领域越来越广,也越来越深入;图形标准API也相应推出一些新特性,提升图形应用的同时兼顾通用计算;GPU硬件厂商也通过这些研究发现不足,从而改进自己的图形处理器。
在GPU上实现流体的计算与仿真是GPGPU在科学计算中应用研究的热点。由于GPU特殊的体系和编程模型,在图形处理器上实现高效的数值仿真需要数值方法具有以下特点:
1)简洁的数据结构。GPU通用计算以纹理作为输入数据,片元程序作为计算核。复杂的数据结构需要在片元程序中计算纹理偏移,保留较多的中间变量,导致计算核计算效率下降。
2)精简的计算步骤。采用多遍绘制需要把输出的数据保存至纹理,以供下一个计算核取用。多遍绘制是个耗时的过程,所以在计算中要尽量减少多遍绘制次数。
3)统一的计算表达。由于GPU采用SIMD的并行计算方式,统一的数据表达有助于减少片元程序中条件和分支语句的使用,提高计算核的效率。
代表性的相关研究工作如下:
[1]Krüger J, Westermann R. Linear Algebra Operators for GPU Implementation of Numerical Algorithms [J]. ACM Trans. on Graphics,2003,22(3):908-916
[2]Harris M J. Fast Fluid Dynamics Simulation on the GPU [A].Fernando R.GPU Gems: Programming Techniques, Tips, and Tricks for Real-Time Graphics[M]. America:Addison-Wesley,2004. pp.637-665
[3]Wu EH, Liu YQ, Liu XH. An Improved Study of Real-time Fluid Simulation on GPU. Journal of Computer Animation & Virtual World (invited paper ofCASA2004), 2004,15(3-4):139~146
[4]Liu Y Q, Liu X H, Wu E H. Real-Time 3D Fluid Simulation on GPU with Complex Obstacles [C]. In Proc. of Pacific Graphics 2004, IEEE Computer Society, Oct. 2004, pp.247-256
[5]Scheidegger C E, Comba J L D, Cunha R D. Navier-Stokes on Programmable Graphics Hardware using SMAC [C] Proceedings of the XVII Brazilian Symposium on Computer Graphics and Image Processing (SIBGRAPI’04),2004,pp.300-307
[6]Li W, Fan Z, Wei XM, Kaufman A. GPU-Based Flow Simulation With Complex Boundaries. Technical Report, Computer Science Department, SUNY at Stony Brook, 2003.
除了[6]中使用Lattice Boltzmann方法外,其余的方法使用的都是经典的计算流体力学数值方法,J. Stam的Stable Fluid方法。该计算方法在图形仿真领域被广泛使用,但是由于数值耗散过大,该方法仅能满足视觉上的效果而不具工程上的指导意义。[5]所采用的MAC方法由于采用显式的方程解法,受到数值稳定性问题的困扰,在应用中受到限制。所以我们希望能够找到一中折中的方法:它在保证求解速度的同时能够相对提高仿真精度。
在计算流体力学(CFD)对非定常不可压流动方程的数值模拟中,通常将速度和压力解耦, 分别求解速度和压力, 常见的有SIMPLE方法和投影方法。SIMPLE 方法在计算非定常流动时, 需要进行很多次内迭代, 计算效率较低, 而投影方法通过预测和校正两步, 就得到了新时刻的速度和压力, 因而具有较高的计算效率。综合GPU计算的特点和已有的工作,我们选取文献[7]Ye T, Mittal R, Udaykumar H S. An Accurate Cartesian Grid Method for Viscous Incompressible Flows with Complex Immersed Boundaries [J]. Journal of Computational Physics,1999,156,209-240的计算方法,在笛卡儿网格下用投影法做不可压流体的数值仿真。为了能理解这篇文献,我们先介绍一些基础的概念
1. Navier-Stokes方程和有限体元离散方法
1822年Navier建立了粘性流体的基本运动方程,后来Stokes完善了该方程,称作Navier-Stokes 方程,是计算流体力学的基础。考虑没有外力作用的粘性不可压流体的Navier-Stokes方程,其控制方程的无量纲形式为:
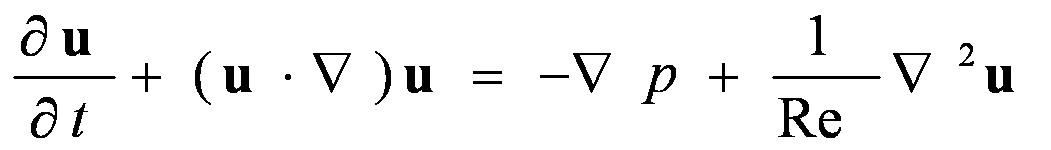
(1)
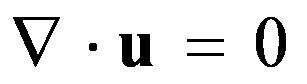
(2)
该方程组由对流场中某一确定的空间区域的受力分析得到,该空间区域称作控制体。控制体的边界称作控制面。其中方程(2-1)由控制体的动量守恒得到,在Navier-Stokes方程组中称为动量方程。方程(2)反映了控制体的质量守恒性质,称作连续性方程。方程中u为速度向量,p为压力,Re为反映流体粘性属性的雷诺系数。在方程(1)中,左边第一项称为时间倒数项,第二项为对流项;右边第一项称为压力梯度项,第二项为粘性耗散项。
在方程(1)两端对控制体进行积分,应用高斯公式后,原微分方程变为如下的积分形式:
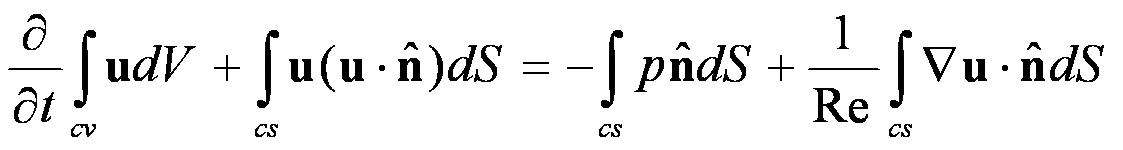
(3)
其中cv代表控制体,cs代表控制面。流场空间由控制面分成有限个的控制体单元,利用高斯公式把变量在控制体内的积分变成在控制面上的积分,该方法称为有限体元离散方法。下图-10所示为流体的变量在2维非交错笛卡儿网格上有限体元离散方法。

图-10
2.Helmholtz-Hodge分解和投影法
Chorin最早提出投影方法(Projection Method),是一种将速度和压力解耦来求解的不可压粘性方程的数值方法。该方法是分为预测-校正的两步:第1步,不考虑不可压条件,在一个估计的压力下求解动量方程得到所谓中间速度场,第2步,将中间速度场进行Helmholtz-Hodge分解,这个过程称为速度场的"投影",由此可以得到满足连续方程的速度场,并对压力场进行修正。该方法又称为分步法(Fractional-Step Method)。
Helmholtz-Hodge分解理论指出,任何一个矢量场w可唯一的分解为一个散度为零的矢量场u和一个标量场p的梯度之和,如(4)所示,其中将(2)代入方程 。所以这个散度为零的矢量场可以如(5)表达。
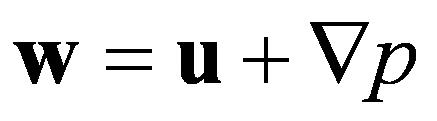
(4)
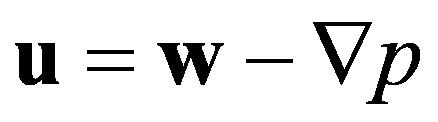
(5)
如果对(4)方程两边求散度,得到(6)的表达,该表达式称为压力泊松方程。
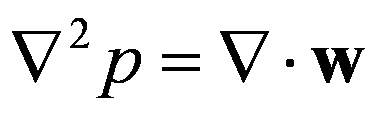
(6)
投影法的分步解法对Navier-Stokes方程采用Helmholtz-Hodge分解,可以将压力项从动量方程中移出,先求解中间速度场w,然后用(6)求解压力场p,最后用(5)对中间速度场进行压力校正,求出最终速度场u。
3.笛卡儿网格下投影法求解非定常流
把上述的方法应用于有限体元离散的形式,可以得到我们使用的方法。对方程(3)的对流项采用Adams-Bashforth 的二阶格式处理,对耗散项采用隐式的Crank-Nicolson方式离散。采用上述的离散方式消除了对粘性稳定性的限制。没有压力梯度项的方程(3),写成半隐式的离散形式如(7)所示:
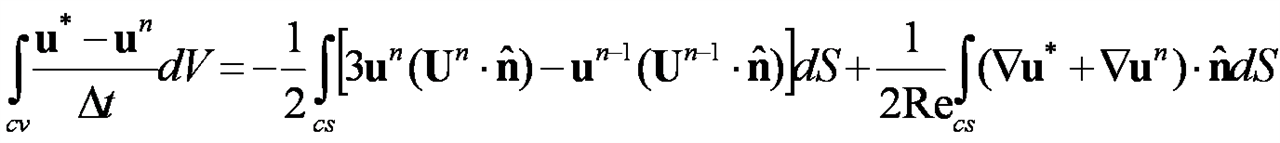
(7)
其中u*表示中间速度场,定义在每个有限体的中心位置,U为控制面速度,定义在每个控制面的中心位置。上标n代表时间步, 表示垂直于边界的外法向量。采用非交错网格如图-10(a)所示,每个有限体元变量位置的定义如图-10(b)所示。方程(7)的中间速度场的边界条件设为物理边界条件,即边界位置的中间速度等于边界位置的下一时刻的实际速度。重写投影方程和连续性方程,可以积分形式下的泊松方程(8),
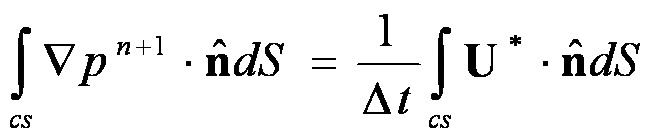
(8)
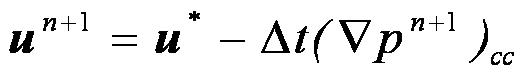
(9)
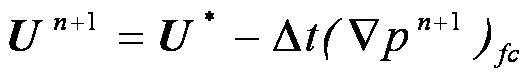
(10)
其中U*为中间速度场的控制面中心的速度,由插值相邻的中间速度得到。该泊松方程的压力边界条件为统一的Neumann边界条件,即边界上压力梯度在外法向上为0。经过(7)和(8)计算中间速度场和压力场之后,最终的速度场由方程(9)(10)得到,其中cc 和fc表示在控制体中心和控制面上求压力的梯度。最终速度的边界条件为 。
当下一时刻的各个场的值都知道后,可以重新开始新一轮计算,在时间上不断推进各个变量。综合以上计算,总的计算过程为以下3步骤:
1)计算迭代中间速度场,方程(7)
2)由中间速度场计算迭代压力场,方程(8)
3)由压力场计算下一时刻速度场,方程(9)(10)

整个操作过程如图-11所示,我们在NVIDIA GeForce 5700 GPU 128MB显存, 128bits带宽,驱动程序版本为66.72;AMD 650MHz CPU 192MB内存,AGP 4X上实现所有的算法。为了使整个计算在32位浮点精度上运行,需要综合使用OPENGL扩展 。GL_NV_texture_rectangle和NV_float_buffer配合使用可得到浮点纹理。WGL_ARB_pbuffer和NV_float_buffer配合使用会得到浮点的pbuffer。WGL_ARB_pbuffer、NV_float_buffer、GL_NV_texture_rectangle、NV_render_texture_rectangle和WGL_ARB_render_texture使用会获得浮点数的绘制到纹理操作。
对 GPU 通用计算流程和OpenGL性能进行测试,我们假定一个多遍绘制的通用计算应用需要如下一些步骤:
1) 初始化数据:在主存中初始化数据空间,给数组赋初值。
2)
初始化第1遍绘制的纹理:把主存中数据传到显存中,用第1步初始化的数组给二维纹理赋初值。
3) 使pbuffer有效,绑定当前纹理
4)
绑定片元程序
5)
并行程序执行:绘制矩形,设纹理坐标,图形管线执行片断程序
6)
获取中间数据:把pbuffer中的数据传递到纹理中,为下一遍绘制作准备。拷贝到纹理,重复5~7步,多遍计算。
7)
返回数据到主存:把存在显存pbuffer中的结果返回到主存中。该步骤可选方法有:7.1)选用pixel_buffer_object,启用DMA传输;7.2)直接使用glReadPixels。
8) 数据后期处理
在Windows XP操作系统下测试整个计算过程,采用同一个简单的线性插值片元程序,分别对128×128、256×256、512×512这3组数据计算进行测试,结果如下表。
通用计算总过程测试表
| 步骤 | 128×128耗时(ms) | 256×256耗时(ms) | 512×512耗时(ms) |
| 1 | 2.753 | 11.270 | 50.194 |
| 2 | 1.764 | 7.522 | 34.276 |
| 3 | 0.631 | 0.559 | 0.573 |
| 4 | 0.016 | 0.021 | 0.018 |
| 5 | 2.534 | 9.277 | 36.490 |
| 6 | 0.062 | 0.065 | 0.077 |
| 7.1 | 0.295 | 0.204 | 0.212 |
| 7.2 | 4.001 | 14.285 | 56.226 |
| 8 | 0.447 | 0.543 | 1.231 |
相关文章推荐
- [物理学与PDEs]第2章习题8 一维定常粘性不可压缩流体的求解
- 计算不可压缩流体- NS方程求解算法
- [物理学与PDEs]第2章习题7 一维不可压理想流体的求解
- GPU对数据的操作不可累加
- 不可表示数求解分析
- 计算不可压缩流体--差分格式的两个问题
- 计算不可压缩流体 -- 数学基础
- 【机器学习】tensorflow: GPU求解带核函数的SVM二分类支持向量机
- 高校科研单位全能超算平台(结构流体电磁仿真/分子动力模拟/多GPU深度学习)最新硬件配置方案
- 计算不可压缩流体 -- 差分/有限体积离散格式
- Q144:FS,求解流体方程(逻辑总结)
- 线性不可分的线性支持向量机的原始问题(凸二次规划)详细求解
- [物理学与PDEs]第2章习题9 粘性流体动能的衰减
- 基于GPU的3D流体模拟
- [物理学与PDEs]第3章习题2 仅受重力作用的定常不可压流理想流体沿流线的一个守恒量
- Simple, Piso, Icofoam等不可压求解器
- 基于GPU的3D流体模拟
- 可重入函数与不可重入函数
- Web 设计师不可错过的 25+ CSS 工具
- 给定固定长度的字符串,求解按字符字典序排列,该字符串是第几小?
